过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（　　）A.x－3y－2＝0 B.x＋3y－2＝0 C.x－3y＋2＝0 D.x＋3y＋2＝0

题目
过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（　　）

A.x－3y－2＝0
B.x＋3y－2＝0
C.x－3y＋2＝0
D.x＋3y＋2＝0
相似考题

1.过点（2，1）且与直线y=0垂直的直线方程为 （ ）A.z=2B.x=1C.y=2D.y=1

2.下列有关直线回归方程Y=a+bX的描述中不正确的是A、决定回归线的两个系数是a和bB、a＞0表示直线与纵轴的交点在原点上方C、b＞0表示直线从左下方走向右上方D、b=0表示直线通过原点E、回归线必通过点（--X，Y）

3.设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。A. B. C. D.

4.以下关于回归方程=b＋bX的描述中错误的是A、b>0表示回归直线与y轴的交点在原点上方B、回归直线未必过点（，）C、b=0，b=0表示回归直线与X轴重叠D、b表示X=0时的值E、b

更多“过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（　　）”相关问题

  • 第1题：

    已知直线L1过点M1(0，0，-1)且平行于X轴，L2过点M2(0，0，1)且垂直于XOZ平面，则到两直线等距离点的轨迹方程为( )。

    A.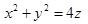
    B.
    C.
    D.

    答案：D
    解析：

  • 第2题：

    过点M0(-1，1)且与曲线2ex-2cosy-1 = 0上点(0，π/3)的切线相垂直的直线方程是：


    答案：C
    解析：
    点斜式求出直线方程。

  • 第3题：

    过点M(3，-2，1)且与直线L :平行的直线方程是：


    答案：D
    解析：
    直线L是平面χ - y- z +1 = 0和平面2χ+ y - 3z + 4 = 0的交线，直线L的方向向量

  • 第4题：

    过点（2，0，－1）且垂直于xOy坐标面的直线方程是（　　）。


    答案：C
    解析：
    垂直于xOy面的直线的方向向量为（0，0，1），由于过点（2，0，－1），则直线的点向式方程为：（x－2）/0＝y/0＝（z＋1）/1。

  • 第5题：

    圆心在Y轴上，且与直线χ+y-3=0及χ-y-1=0都相切的圆的方程为_____．


    答案：
    解析：
    【答案】
    【考情点拨】本题主要考查的知识点为圆的切线的性质．
    【指导指导】设圆的方程为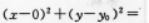r2(如图)

  • 第6题：

    直线l1与直线l2：3x+2y-12=0的交点在x轴上，且l1⊥l2，则l1在y轴上的截距是（）



    答案：B
    解析：

  • 第7题：

    以直线y十x=0为对称轴且与直线y-3x=2对称的直线方程为（ ）


    答案：A
    解析：

  • 第8题：

    已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：



    答案：A
    解析：
    提示 求出过M1，M2，M3三点平面的法线向量。



    @##

  • 第9题：

    已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为（ ）。


    答案：B
    解析：
    正确答案是B。
    提示：平面π的法向量，所求直线的方向向量为i+k ,故应选B。

  • 第10题：

    以下关于回归方程=b+bX的描述中错误的是（）。

    • A、b>0表示回归直线与y轴的交点在原点上方
    • B、回归直线未必过点（，）
    • C、b=0，b=0表示回归直线与X轴重叠
    • D、b表示X=0时的值
    • E、b<0表示回归直线从左上方走向右下方

    正确答案:B

  • 第11题：

    单选题
    过点（1，2）且与直线2x＋y－3＝0平行的直线方程为（　　）．
    A

    2x＋y－5＝0

    B

    2y－x－3＝0

    C

    2x＋y－4＝0

    D

    2x－y＝0


    正确答案： B
    解析：
    设和2x＋y－3＝0平行的直线方程为2x＋y＋c＝0，将（1，2）代人，则有2×1＋2＋c＝0，得c＝－4．

  • 第12题：

    问答题
    求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。

    正确答案：
    过点M(-1,0,1)且垂直于直线(x-2)/3=(y+1)/(-4)=z/1的平面方程为3x-4y+z+2=0。该平面与直线(x+1)/1=(y-3)/1=z/2的交点为(12,16,26),则该交点与点M(-1,0,1)形成的直线方程为(x+1)/13=y/16=(z-1)/25,即为所求。
    解析： 暂无解析

  • 第13题：

    设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面：
    (A)平行 （B)垂直 (C)重合 (L)相交但不垂直


    答案：D
    解析：
    解：选D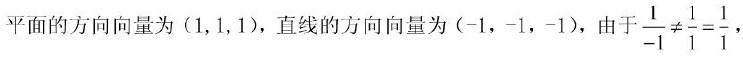
    所以直线与平面不垂直。又1x(-1) + 1x1+1x1=1≠0，所以直线与平面不平行。

  • 第14题：

    已知平面π过点(1，1，0)、(0，0，1)、(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为 ( )。



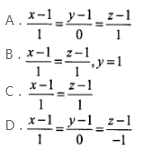    答案：B
    解析：
    平面π的法向量所求直线的方向向量为i+k，故应选B。@##

  • 第15题：

    设直线L过A(1，0，0)，B(0，1，1)两点，将L绕z轴旋转一周得到曲面∑，∑与平面z=0，z=2所围成的立体为Ω.
    　　(Ⅰ)求曲面∑的方程；
    　　(Ⅱ)求Ω的形心坐标.


    答案：
    解析：
    【分析】利用定义求旋转曲面∑的方程；利用三重积分求Ω的形心坐标.

  • 第16题：

    下列有关直线回归方程Y=a+bX的描述中不正确的是

    A.a＞0表示直线与纵轴的交点在原点上方
    B.b=0表示直线通过原点
    C.决定回归线的两个系数是a和b
    D.b＞0表示直线从左下方走向右上方
    E.回归线必通过点（--X，Y）

    答案：B
    解析：

  • 第17题：

    过点(0，1)且与直线x+y+1=0垂直的直线方程为()

    A.y=x
    B.y=2x+1
    C.y=x+1
    D.y=x-1

    答案：C
    解析：

  • 第18题：

    与已知直线7x+24y-5=0平行，且距离等于3的直线方程是。


    答案：
    解析：
    7x+24y+70=0或7x+24y-80=0

  • 第19题：

    对于直线回归方程y=bo+bx，以下说法正确的是( )。

    A.截距b0＞0，表示回归直线与纵轴的交点在原点下方
    B.截距b0＜0，表示回归直线与纵轴的交点在原点下方
    C.截距bo=0，表示回归直线通过原点
    D.b=0，表示回归直线平行于x轴
    E.b=0，表示回归直线垂直于x轴

    答案：B,C,D
    解析：
    截距bo＞0，表示回归直线与纵轴的交点应当在原点上方。b=o，表示回归直线平行于x轴，即y与x无线性依存关系。

  • 第20题：

    试求通过点Mo(一1，0，4)，垂直于平面Ⅱ：3x一4y-10=0，且与直线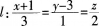
    平行的平面方程。


    答案：
    解析：
    平面Ⅱ的法向量m=（3-4，1)，直线Z的方向向量l=(3，l，2)，所以所求平面的法向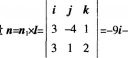

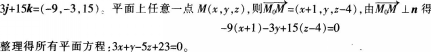
  • 第21题：

    已知中心在坐标原点0的椭圆C经过点A(2，3)且点F(2，0)为其右焦点。
    (1)求椭圆C的方程；
    (2)是否存在平行于OA的直线l，使l与椭圆C有公共点，且直线OA与l的距离等于4，若存在，求l方程；若不存在，请证明。


    答案：
    解析：

  • 第22题：

    单选题
    过点（2，1）且与直线y＝0垂直的直线方程为（　　）．
    A

    x＝2

    B

    x＝1

    C

    y＝2

    D

    x＝1


    正确答案： D
    解析：
    直线y＝0即为x轴，所求直线要与x轴垂直，即为x＝2．

  • 第23题：

    单选题
    直线ax—by＋ab＝o（其中ab≠0）与y轴的交点坐标是（　　）．
    A

    （0，－b）

    B

    （0，b）

    C

    （0，－a）

    D

    （0，a）


    正确答案： A
    解析：
    由题意得，设交点坐标为（0，y1），则－by1＋ab＝0，∵ab≠0，∴b≠0．∴y1＝a，交点坐标为（0，a）．

相关内容