如图所示，在竖直平面内有一光滑的圆形轨道，轨道的半径为R，一小球可在轨道内侧做圆周运动，且在通过圆周顶端的A点时不脱离轨道掉下来。则：（1）小球通过A点的最小速度v0为多大? （2）在小球以速度v0通过A点的情况下，小球运动到B点时对轨道的压力F为多大?

题目

如图所示，在竖直平面内有一光滑的圆形轨道，轨道的半径为R，一小球可在轨道内侧做圆周运动，且在通过圆周顶端的A点时不脱离轨道掉下来。则：
（1）小球通过A点的最小速度v0为多大?
（2）在小球以速度v0通过A点的情况下，小球运动到B点时对轨道的压力F为多大?

相似考题

1.一质量为的小球,沿光滑环形轨道由静止开始下滑,若足够高,则小球在最低点时,环对其作用力与小球在最高点时环对其作用力之差,恰好是小球重量的()A、2倍B、4倍C、6倍D、8倍

2.一细线拴着一小球，小球绕固定点在竖直平面内做圆周运动．设小球运动到最低点时所受细线拉力的大小为厂已知小球所受重力的大小为G，则（　　）

3.如图5—17所示，在竖直平面内有一光滑的圆形轨道，轨道半径为尺，一个小球可在轨道内侧做圆周运动，且在通过圆周顶端的A点时不脱离轨道掉下来. （1）小球通过A点的最小速度V0为多大（2）在小球以速度V0通过A点的情况下，小球运动到B点时对轨道的压力F为多大

4.宇宙飞船在半径为R。的轨道上运行，变轨后的半径为R2，R1>R2。宇宙飞船绕地球做匀速圆周运动，则变轨后宇宙飞船的A．线速度变小 B．角速度变小C．周期变大 D．向心加速度变大

更多“如图所示，在竖直平面内有一光滑的圆形轨道，轨道的半径为R，一小球可在轨道内侧做圆周运动，且在通过圆周顶端的A点时不脱离轨道掉下来。则：（1）小球通过A点的最小速度v0为多大? （2）在小球以速度v0通过A点的情况下，小球运动到B点时对轨道的压力F为多大?”相关问题

第1题：

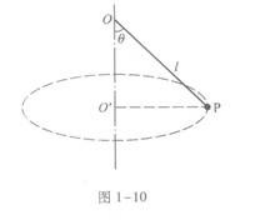
如图1-10所示，细线的上端固定于O点，下端系一个小球P，线长l＝
1.56 m，已知小球在水平面内做以O'为圆心的匀速圆周运动，悬线与竖直方向的夹角θ=45°．求

答案：
解析：
5.0 rad/s 【解题指要】本题是匀速圆周运动的试题，它的考点有牛顿第二定律和向心力．
以小球为研究对象，小球受两个作用力，细线的拉力FT和重力G．FT沿细线向上，G竖直向下，图1－17是它的受力图．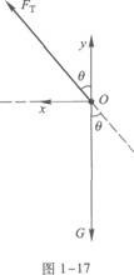

小球在水平面内做匀速圆周运动，它所受的合外力是匀速圆周运动的向心力．因此，重力G和拉力FT的合力就是向心力F．
取平面直角坐标如图所示．
FT的分量为
FTX=FTsinθ
FTY=FTcosθ
G的分量为
Gx=0
Gy=－mg
水平方向的牛顿方程为
FTx=FTsinθ=F=ma①
竖直方向的牛顿方程为
FTy+Gy=FTcosθ－mg＝0
即FTy=FTcosθ=mg②
由式①、②解得
F=mgtanθ=ma
把向心加速度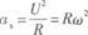

代入上式得
F=mRω2=mgtanθ
因此角速度为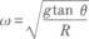

圆周运动半径R与线长l的关系是
R=lsinθ
代入上式解得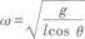

代入题给数值，算得
第2题：

一个小球在竖直平面内的光滑圆环做圆周运动，小球经过圆环最高点时刚好不脱离圆环，通过最高点时，小球（）。

A.没有受到向心力
B.向心力等于重力
C.没有向心加速度
D.线速度为0

答案：B
解析：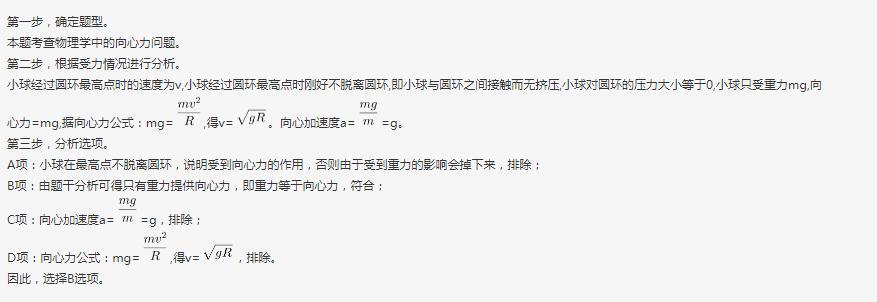
第3题：

阅读案例，并回答问题。
下面是某同学对课后习题的解答过程：
如图所示，正电荷q1固定于半径为R的半圆光滑轨道的圆心处，将另一带正电、电荷量为q2,质量为m的小球，从轨道的A处无初速度释放，求：
(1)小球运动到B点时的速度大小；(2)小球在B点时对轨道的压力。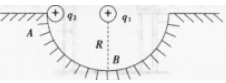

解：(1)设小球通过轨道最低点时的速度大小为V，小球从A到B的过程中只有重力做功，根据动能定理得：
(2)以小球为研究对象，对其受力分析。小球受重力、支持力与电场力，则有：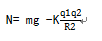
问题：
(1)指出此道试题检测了学生所学的哪些知识点。
(2)指出学生解答中的错误，分析错误产生的可能原因，给出正确解法。
(3)给出一个教学思路，帮助学生掌握相关知识。

答案：
解析：
(1)本题考查受力分析、牛顿第二定律、牛顿第三定律、圆周运动、动能定理、库仑定律。 (2)学生已经掌握了题干中电场力做功的情形，并正确求出小球在B点的速度，但是忽略了小球是傲圆月运动，其所受合力提供向心力。另外应该标明，小球受到的支持力和小球对轨道的压力大小相等，方向相反。
正确解法为：
①设小球通过轨道最低点时的速度大小为V，小球从A到B的过程中只有重力做功，根据动能定理得：

(3)针对此学生，教师可以通过一系列启发性的问题，引导学生回忆圆周运动的知识。学生已经掌握了点电荷形成的电场中电场力做功情况，教师可从分析物体受力、研究物体运动状态、分析整个过程中的功能转换等角度加深学生对相关知识的理解和认识。
第4题：

小球m用长为L的悬线固定在O点，在O点正下方处有一个光滑钉子C，如图所示，今把小球拉到悬线成水平后无初速度地释放.当悬线成竖直状态且与钉子相碰时()。

答案：C
解析：
绳在竖直方向上与钉子相碰瞬间，绳子的拉力和重力都不对小球做功，即小球的动能不
第5题：

如图所示。小球沿水平面以初速度υo通过O点进入半径为R的竖直半圆弧轨道，不计一切阻力，下列说法正确的是（　　）。
A．球进入竖直半圆弧轨道后做匀速圆周运动
B．若小球能通过半圆弧最高点P，则球运动到P时向心力恰好为零
C．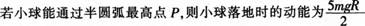
D．若小球恰能通过半圆弧最高点P，则小球落地点离O点的水平距离为2R

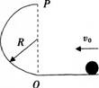答案：D
解析：
进入半圆弧轨道后，小球受到轨道的弹力和重力的作用，重力方向竖直向下，因此小球不能做匀速圆周运动，A错。小球能通过圆弧的最高点，因此速度必不为零，向心力也不为零，落地时的动能可能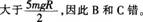
第6题：

如图所示，在“嫦娥”探月工程中，设月球半径为R，月球表面的重力加速度为g0。飞船在半径为4R的圆型轨道Ⅰ上运动，到达轨道的A点时点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B时，再次点火进入近月轨道Ⅲ绕月做圆周运动，则( )。

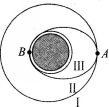
A①飞船在轨道Ⅲ的运行速率大于(g0R)1/2
B②飞船在轨道l上运行速率小于在轨道Ⅱ上B处的速率
C③飞船在轨道l上的重力加速度小于在轨道Ⅱ上B处重力加速度
D④飞船在轨道l、轨道Ⅲ上运行的周期之比有T1：TⅢ=4：1

答案：B
解析：
第7题：

阅读案例，并回答问题。
下面是某同学对课后习题的解答过程：
如图所示，正电荷q1固定于半径为R的半圆光滑轨道的圆心处，将另一带正电、电荷量为q2、质量为m的小球，从轨道的A处无初速度释放，求：
(1)小球运动到B点时的速度大小；(2)小球在B点时对轨道的压力。

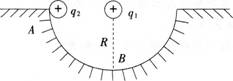
解：(1)设小球通过轨道最低点时的速度大小为υ，小球从A到B的过程中只有重力做功，根据动能定理得：

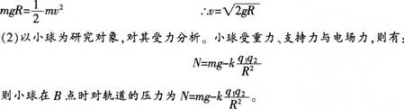
问题：(1)指出学生解答中的错误，分析错误产生的可能原因，给出正确解法。
(2)给出一个教学思路，帮助学生掌握相关知识。

答案：
解析：
(1)学生已经掌握了题干中电场力做功的情形，并正确求出小球在B点的速度，但是忽了小球是做圆周运动，其所受合力提供向心力。另外应该标明，小球受到的支持力和小球对轨道的压力大小相等，方向相反。正确解法为：

(2)针对此学生，教师可以通过一系列启发性的问题，引导学生回忆圆周运动的知识。学生已经掌握了点电荷形成的电场中电场力做功情况，教师可适当进行语言上的鼓励。教师可从分析物体受力、研究物体运动状态、分析整个过程中的功能转换等角度加深学生对相关知识的理解和认识。
第8题：

以v₀＝20m/s的速度竖直上抛一小球，经2s以相同的初速度在同一点竖直上抛另一小球．g取10m/s²，则两球相碰处离出发点的高度是（）
- A、10m
- B、15m
- C、20m
- D、不会相碰
正确答案:B
第9题：

在水平面内作匀速圆周运动的物体，下列各种论述中是否有错误，如果有错误请改正并指明理由：（1）在圆轨道的各点上它的速度相等（2）在圆轨道的各点上它受的力相等（3）在圆轨道的各点上它的动量相等（4）在圆轨道的各点上它对圆心的角动量相等（5）在圆轨道的各点上它的动能相等

正确答案: （1）错误，速度不相等，因方向变化；
（2）错误，受力不相等，因方向变化；
（3）错误，动量不相等，因方向变化；
（4）正确；
（5）正确。
第10题：

填空题
将轨道BC段改为水平，如图乙所示．小球仍从A点静止释放，小球经过M点时的机械能大于、小于还是等于其在A点的机械能？____．

正确答案：等于;
解析：
由于不存在其他阻力的情况，其机械能是守恒的，因此A点机械能等于M点机械能．
第11题：

多选题
关于地球在绕日公转的下列说法，正确的是（）。
A
太阳中心位于地球轨道椭圆的一个焦点上，这一点也是其他行星轨道椭圆的焦点之一
B
公转是一种转动，即圆周运动
C
春分日，地球位于地球轨道椭圆的中距点
D
地球过近日点时，速度最快；而过远日点时，速度最慢，但面积速度不变

正确答案： C,A
解析：暂无解析
第12题：

单选题
A
不论在轨道1还是在轨道2运行，卫星在P点的速度都相同
B
不论在轨道1还是在轨道2运行，卫星在P点的加速度都相同
C
卫星在轨道1的任何位置都具有相同加速度
D
卫星在轨道2的任何位置都具有相同动量

正确答案： B
解析：暂无解析
第13题：

A.球进入竖直半圆弧轨道后做匀速圆周运动
B.若小球能通过半圆弧最高点P，则球运动到P时向心力恰好为零
C.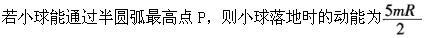
D.若小球恰能通过半圆弧最高点P，则小球落地点离O点的水平距离为2R

答案：D
解析：
第14题：

如右图，正方形的迷你轨道边长为1米，1号电子机器人从点A以1米/秒的速度顺时针绕轨道移动，2号电子机器人从点A以3米/秒的速度逆时针绕轨道移动，则它们的第2017次相遇在：

A.点A
B.点C
C.点B
D.点D

答案：D
解析：
第一步，本题考查行程问题，属于相遇追及类。
第二步，第1秒1号机器人顺时针走到点D，2号逆时针走到点D，故两个机器人每过1秒相遇一次，相遇点依次为D—C—B—A—D—C—B—A……每4次相遇为一个周期。
第三步，2017÷4＝504…1，则第2017次相遇与第1次相遇地点是同一地点，即D点。
第15题：

小球m用长为L的悬线固定在O点，在O点正下方处有一个光滑钉子C，如图所示，今把小球拉到悬线成水平后无初速度地释放．当悬线成竖直状态且与钉子相碰时（）。

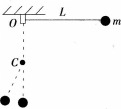A．小球的线速度突然增大
B．小球的角速度突然减小
C．小球的向心加速度突然增大
D．悬线的拉力突然减小

答案：C
解析：
绳在竖直方向上与钉子相碰瞬间，绳子的拉力和重力都不对小球做功，即小球的动能不
第16题：

如图5所示，半径为R的刚性圆环轨道，水平固定在光滑的桌面上．一物体贴着轨道内侧运动，物体与轨道间的滑动摩擦系数为μ。设物体在某时刻经过A点时的速率为V0，求：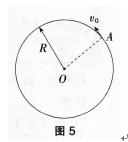

(1)此后t时刻物体的速率。
(2)从A点开始在t时间内的路程。

答案：
解析：
(1)物体贴着轨道内侧运动，在水平面上受两个力的作用，一是环对物体的正压力Ⅳ，方向指向环心，另一个是环对物体的滑动摩擦力f，方向沿圆环的切向方向。建立自然坐标系，并应用牛顿第二定律的法向分量式和切向分量式：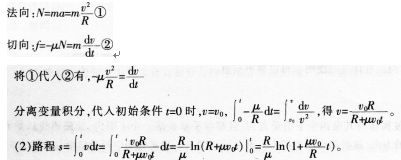
第17题：

如图所示，MN为半径较大的光滑圆弧轨道的一部分，把小球A放在MN的圆心处，再把另一小球B放在MN上离最低点C很近的B处，今使两球同时自由释放，则在不计空气阻力时有（　　）。

A．A球先到达C点
B．B球先到达C点
C．两球同时到达C点
D．无法确定哪一个球先到达C点

答案：A
解析：
第18题：

如图所示，小球沿水平面以初速度v0通过O点进入半径为R的竖直半圆弧轨道，不计一切阻力，下列说法正确的是( )。

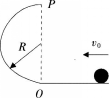
A．球进入竖直半圆弧轨道后做匀速圆周运动
B．若小球能通过半圆弧最高点P.则球运动到P时向心力恰好为零
C．若小球能通过半圆弧最高点P,则小球落地时的动能为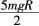

D．若小球恰能通过半圆弧最高点P，则小球落地点离O点的水平距离为2R

答案：D
解析：
进入半圆弧轨道后，小球受到轨道的弹力和重力的作用，重力方向竖直向下，因此小球不能做匀速圆周运动，A错。小球能通过圆弧的最高点，因此速度必不为零，向心力也不为零，落地时的动能可能大于

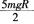
因此B和C错。
第19题：

如图所示圆环以角速度ω绕铅直轴AC自由转动，圆环的半径为R，对转轴的转动惯量为I；在圆环中的A点放一质量为m的小球，设由于微小的干扰，小球离开A点。忽略一切摩擦，则当小球达到B点时，圆环的角速度是（　　）。

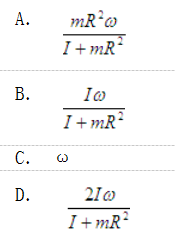答案：B
解析：
第20题：

按玻尔的氢原子理论，电了在以质子为中心，半径为r的圆形轨道上运动，把这样一个原子放在均匀的外磁场中，使电子轨道平面与B垂直，在r不变的情况下，电子轨道运动角速度将（）。
- A、增加
- B、减小
- C、不变
- D、改变方向
正确答案:A
第21题：

一电子在垂直于均匀磁场的方向做半径为R=1.2cm的圆周运动，电子速度v=10⁴m·s^-1．求圆轨道内所包围的磁通量是多少？

正确答案:电子所带的电量为e=1.6×10^-19库仑，质量为m=9.1×10^-31千克.
电子在磁场所受的洛伦兹力成为电子做圆周运动的向心力，即：f=evB=mv²/R，所以B=mv/eR.
电子轨道所包围的面积为S=πR²，磁通量为Φ=BS=πmvR/e=2.14×10^-9（Wb）.
第22题：

多选题
如图所示，在垂直纸面向里的匀强磁场中有三个带电粒子，它们在纸面内沿逆时针方向做匀速圆周运动，其中1和2为质子的轨迹，3为α粒子（氦核）的轨迹．三者的轨道半径关系为R 1＞R 2＞R 3，并相切于P点．设v、a、T、F分别表示它们做圆周运动的线速度、加速度、周期和所受的洛伦兹力的大小，则下列判断正确的是（）
A
v ₁＞v ₁＞v ₃
B
a ₁＞a ₂＞a ₃
C
T ₁＜T ₂＜T ₃
D
F ₁=F ₂=F ₃

正确答案： D,C
解析：暂无解析
第23题：

单选题
A
球进入竖直半圆弧轨道后做匀速圆周运动
B
若小球能通过半圆孤最高点P.则球运动到P时向心力恰好为零
C
若小球能通过半圆弧最高点P.则小球落地时的动能为5mgR/2
D
若小球恰能通过半圆弧最高点P.则小球落地点离D点的水平距离为2R

正确答案： D
解析：

题目

相似考题

相关内容