甲完成一项工作需t小时，乙完成同样工作比甲少用1小时，乙的工作效率为_______

题目

甲完成一项工作需t小时，乙完成同样工作比甲少用1小时，乙的工作效率为_______

相似考题

1.设分别X,Y表示甲乙两个人完成某项工作所需的时间,若EXDY则()A、甲的工作效率较高，但稳定性较差B、甲的工作效率较低，但稳定性较好C、甲的工作效率及稳定性都比乙好D、甲的工作效率及稳定性都不如乙

2.：一件工作甲、乙合做30小时可以完成，共同做了6小时后甲因事离开，由乙继续做了40小时才完成，如果这项工作由甲单独做要多少小时完成？（ ）A．75B．72C．69D．66

3.甲、乙同时开始做一批零件，4天后，甲完成了总数的1/5，乙比甲多完成了20个。此后乙 因事退出，甲将工作效率提高一倍，5天后完成了任务。问甲共做了多少个零件? A．120 B．130 C．140 D．160

4.有一件工作，丙单独做需10小时完成;乙、丙合作需4小时完成。甲2小时完成的工作量，乙需要3小时才能完成。现在这件工作由丙独做，他从清晨5时开工，必须在中午12时完工。甲、乙二人应帮助丙工作多少时间才能使丙准时完成工作?()A.4/5小时B.1小时C.4/3小时D.2小时

参考答案和解析

设一项工作为1

乙完成工作需t-1小时

乙的工作效率为1/ (t-1)


更多“甲完成一项工作需t小时，乙完成同样工作比甲少用1小时，乙的工作效率为_______”相关问题

  • 第1题：

    一项工作，甲先做6小时乙再做12小时可以完成，甲先做8小时乙再做6小时也可以完成。如果甲先做3小时接着由乙做，那么还需要多少小时才能完成? A．12 B．15 C．18 D．21


    正确答案：D
    由条件可知，甲多做2个小时，乙就少做6个小时，甲乙工效之比为3：1。与第一种情况相比，甲少做了3个小时，则乙需要多做3×3＝9个小时，所以乙还需12+9＝21小时才能完成。
    另解：设乙每小时的工作量为1，甲的工作量为x，那么6x+12＝8x+6，解得x＝3，总的工作量为6×3+12＝30，那么甲工作3小时后，乙还需要30－3×3＝21小时完成。

  • 第2题：

    抄一份书稿，甲每天的工作效率等于乙、丙二人每天工作效率的和；丙的工作效率相当于甲、乙每天工作效率和的1/5；如果三人合抄只需8天就完成了，那么乙一人单独抄需要多少天才能完成?（ ）

    A．24

    B．20

    C．18

    D．12


    正确答案：A

  • 第3题：

    抄一份书稿，甲每天的工作效率等于乙、丙二人每天的工作效率之和；丙每天的工作效率相当于甲、乙二人每天的工作效率之和的1/5；如果三人合抄需要8天就能完成，那么乙一人单独抄需要多少天才能完成？（ ）

    A．24

    B．21

    C．20

    D．18


    正确答案：A

  • 第4题：

    单独完成某项工作，甲需要 16 小时，乙需要12小时，如果按照甲、乙、甲、乙??的顺序轮流工作，每次1 小时，那么完成这项工作需要多长时间？

    A．13 小时 40 分钟

    B．13小时 45分钟

    C．13 小时 50分钟

    D．14小时


    正确答案：B
    9．B．［解析］本题为工程类题目。设总工程量为48，则甲的效率是 3，乙的效率是 4，工作 12 小时后，完成了42。第 13小时甲做了 3，完成了总工程量 45，剩余的3由乙在第十四小时完成。在第十四小时里，乙所用的时间是 3/4小时，所以总时间是 13.75小时。

  • 第5题：

    单独完成某项工作，甲需要 16 小时，乙需要 12 小时，如果按照甲、乙、甲、 乙、??的顺序轮流工作，每次 1 小时，那么完成这项工作需要多长时间？

    A. 13 小时 40 分钟
    B. 13 小时 45 分钟
    C. 13 小时 50 分钟
    D. 14 小时

    答案：B
    解析：
    甲乙各工作一小时可完成 1/16+ 1/12=7/48 ，各工作 7 个小时的时候多做了 7/48*7-1=1/48，即乙多工作了 12/48=1/4小时，所以，完成这项工作共需要 13 小时 45 分钟。故答案为B。

  • 第6题：

    校对一份书稿，编辑甲每天的工作效率等于编辑乙、丙每天工作效率之和，丙的工作效率相当于甲、乙每天工作效率之和的。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿，则需要（ ）天才能完成。
    A. 20 B. 16 C. 24 D. 18


    答案：D
    解析：

  • 第7题：

    甲、乙两个工程队合作完成某工程需36天，若甲工程队先做10天，剩下的工程再由两队合作30天完成。问乙工程队的工作效率是甲工程队的：


    答案：A
    解析：
    第一步，本题考查工程问题，属于时间类。
    第二步，设甲、乙工程队的工作效率分别为x、y，根据题意可列出等式：36（x＋y）＝10x＋30（x＋y），化简得y∶x＝2∶3。
    因此，选择A选项。

  • 第8题：

    某项工程若由甲、乙两队合作需105天完成，甲、丙两队合作需60天，丙、丁两对合作需70天，甲、丁两对合作需84天。问这四个工程的工作效率由低到高的顺序是什么：
    A乙丁甲丙
    B乙甲丙丁
    C丁乙丙甲
    D乙丁丙甲


    答案：A
    解析：
    解析
    根据题干条件，甲丙合作需要60天，甲丁合作需要84天，甲的工作效率一定，故可推知丙的效率要高于丁的效率，由此排除B项；丙丁合作需要70天，甲丁合作需要84天，同理可以推知，丙的效率应高于甲的效率，由此排除C、D，只有A项符合。
    故正确答案为A。

  • 第9题：

    甲、乙两队合作一项工程，按原来的工作效率，甲队单独完成比乙队单独完成少用了3天；现在甲队提高工效20％，乙队提高工效25％；这样甲队单独完成只比乙队单独完成少用2天。如果工作效率提高后，先由乙队单独做1天，然后两队合作，还需多少天完成?

    A.4
    B.5
    C.6
    D.7

    答案：B
    解析：
    设按原来的工作效率甲单独完成需要x天，则乙单独完成需要(x+3)天，提高效率后，甲

  • 第10题：

    一项工作，甲、乙合作20小时可以完成，已知甲与乙的速度比为5：4，则甲单独完成这项工作需要的小时数为（）。

    • A、45
    • B、40
    • C、39
    • D、36

    正确答案:D

  • 第11题：

    单选题
    有一项工作，甲单独干需要10小时能完成。乙单独干需要12小时能完成，甲乙两人同时工作5小时后，甲另有其他的事情去做，只有乙继续工作，那么完成这项工作共用了（  ）小时。
    A

    5

    B

    6

    C

    7

    D

    8


    正确答案： D
    解析：

  • 第12题：

    单选题
    有一项工作，甲单干需要10个小时完成，乙单干需要12个小时完成。甲、乙两人同时工作5小时后，甲另有其他的事情去做，只有乙继续工作，那么完成这项工作共用了（）小时。
    A

    5

    B

    6

    C

    7

    D

    8


    正确答案： D
    解析：

  • 第13题：

    单独完成某项工作,甲需要16小时,乙需要12小时,如果按照甲、乙、甲、乙、……的顺序轮流工作,每次1

    单独完成某项工作，甲需要１６小时，乙需要１２小时，如果按照甲、乙、甲、乙、……的顺序轮流工作，每次１小时，那么完成这项工作需要多长时间？（    ）

    Ａ．１３小时４０分钟     Ｂ．１３小时４５分钟

    Ｃ．１３小时５０分钟      Ｄ．１４小时


    【正确答案】B
    【思路点拨】由题意可知，此项工作若甲乙各做一小时，每两小时可完成整项工作的1/16+1/12=7/48，当工作13小时时，甲乙共做了整项工作的7/48×6+1/16=45/48，剩余部分乙再做45分钟即可完成，故选择B选项

  • 第14题：

    某项工作，若甲单独做需40天完成，乙单独做需24天完成，如果乙先做12天，再由甲去完成，问甲还要做几天可以完成全部工作?(   ) 

    A. 13    B. 20    C. 14     D. 18

     


    B 
    设全部工作为1,则甲每天完成的量是1/40,乙则是1/24,由此可知(1-1/24×12)÷1/40=20天，故选B。

  • 第15题：

    甲、乙两名职工接受相同工作量的文稿录入任务。甲平均每小时录入3600字，乙平均每小时录入3000字。两人同时开始录入，甲比乙提早2.5小时完成任务。当甲完成任务时，乙录入了(24)字。

    A．15000

    B．22500

    C．37500

    D．45000


    正确答案：C
    解析：解法1：依题意，当甲完成任务时，甲比乙多录入的字数为3000×2.5=7500字。
      由此可知，甲完成任务所用的时间为7500÷(3600-3000)=12.5小时。
      当甲完成任务时，乙录入的字数为3000×12.5=37500字。
      解法2：假设甲、乙完成该录入任务所花的时间分别为x、y小时，依题意得，
     
      解得x=12.5。
      当甲完成任务时，乙录入的字数为3000x=3000×12.5=37500字。

  • 第16题：

    一项工作，甲先做6小时乙再做12小时可以完成，甲先做8小时乙再做6小时也可以完成。如果甲先做3小时接着由乙做，那么还需要多少小时才能完成?

    A．12

    B．15

    C．18

    D．21


    正确答案：D
    设乙每小时的工作量为l，甲的工作量为x，那么6x+12=8x+6，解得x=3，总的工作量为6×3+12：30．那么甲工作3小时后．乙还需要30-3×3=21小时完成。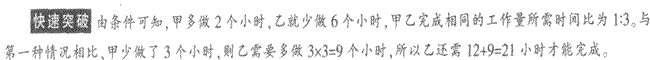

  • 第17题：

    有甲、乙、丙三组工人，甲组4人的工作，乙组需5人完成；乙组3人的工作．丙组需8人完成。一项工作，需甲组13人、乙组l5人合作3天完成，如果让丙组10人去做，需要多少天完成?

    A.20
    B.22
    C.24
    D.25

    答案：D
    解析：
    甲、乙组每个工人的工作效率之比为5：4，乙、丙组每个工人的工作效率之比为8：3，则三组每个工人的工作效率之比为10：8：3。设三组每个工人的工作效率分别为l0、8、3，则这项工作的工作量为(13×10+15×8) ×3=750，则丙组需要做750+(3×10)=25天，应选择D。

  • 第18题：

    甲、乙合作完成一项工作，由于配合得好，甲的工作效率比独做时提高了1/10,乙工作效率 比独做时提高了1/5,甲、乙两人合作4小时，完成全部工作的2/5.第二天乙又独做了 4小时，还剩下这件工作的13/30没完成。这项工作甲独做需要几个小时才能完成？（ ）

    A. 16
    B. 8
    C. 22
    D. 30

    答案：C
    解析：
    乙独做4小时完成全部工程的1一2/5-13/30=1/6,则乙独做时甲的工作效率为

  • 第19题：

    甲、乙、丙、丁四个工厂联合完成一批玩具的生产任务，如果四个工厂同事工作，需要10个工作日完成；如果交给甲、乙两个工厂，需要24个工作日完成；如果交给乙、丙两个工厂，所需时间比交给甲、乙两个工厂少用15个工作日。已知甲、乙两厂每天生产的件数差与丙、丁两厂每天生产的件数差相同，问如果单独交给丁工厂，需要多少个工作日完成：
    A30
    B48
    C60
    D80


    答案：B
    解析：

  • 第20题：

    某项工作，甲单独做需10天完成，乙单独做需6天完成。如果甲先做2天，然后乙接替甲做2天．再由甲接替乙做2天……两人如此交替工作。那么，完成此项工作共用多少天?

    A.6
    B.7
    C.8
    D.9

    答案：C
    解析：

  • 第21题：

    有一项工作，甲单位干需要10小时能完成。乙单位干需要12小时能完成，甲乙两人同时工作5小时后，甲另有其他的事情去做，只有乙继续工作，那么完成这项工作共用啦（）小时。

    A. 5
    B. 6
    C. 7
    D. 8

    答案：B
    解析：
    赋值工作总量为时间的公倍数60。那么甲的效率是6，乙的效率是5。两人共同工作5小时，即工作了



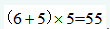
    还剩下



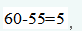
    乙还需要1小时完成。则共用了5+1=6（小时）。选择B。

  • 第22题：

    甲、乙两个加工小组分别完成一项加工任务，甲组单独完成需要6天，乙组单独完成需要8天，甲组与乙组的工作效率之比是（）

    • A、4：3
    • B、6：8
    • C、3：4

    正确答案:A

  • 第23题：

    单选题
    一项工作，甲、乙合作20小时可以完成，已知甲与乙的速度比为5：4，则甲单独完成这项工作需要的小时数为（）。
    A

    45

    B

    40

    C

    39

    D

    36


    正确答案： B
    解析： 工程问题--比例法。甲与乙的速度比为5：4，则甲与甲、乙合作速度比为5：9，则甲单独完成的时间与甲、乙合作完成时间比为9：5；甲、乙合作20小时可以完成，则甲单独完成所用时间为20÷5÷9=36小时，故选D。

相关内容