根据下列条件,分别确定二次函数的解析式:(1)抛物线y=ax²+bx+c过点(-3,2),(-1,-1),(1,3);
题目
根据下列条件,分别确定二次函数的解析式:
(1)抛物线y=ax²+bx+c过点(-3,2),(-1,-1),(1,3);
相似考题
参考答案和解析
更多“根据下列条件,分别确定二次函数的解析式:(1)抛物线y=ax²+bx+c过点(-3,2),(-1,-1),(1,3);”相关问题
-
第1题:
下列情形时,如果a>0,抛物线y=ax²+bx+c的顶点在什么位置?
(1)方程ax²+bx+c=0有两个不等的实数根;
(2)方程ax²+bx+c=0有两个相等的实数根;
(3)方程ax²+bx+c=0无实数根。
如果a<0呢?
∵a>0,∴抛物线开口向上。
(1)∵ax²+bx+c=0有两个不等实根。
∴图象与x轴有两个交点。∴顶点在x轴下方。
(2)∵ax²+bx+c=0有两个相等实根。
∴图象与x轴有且只有一个交点。∴顶点在x轴上。
(3)∵ax²+bx+c=0无实根。
∴图象与x轴无交点。∴顶点在x轴上方。
a0时,(1)顶点在x轴上方;
(2)顶点在x轴上;
(3)顶点在x轴下方。
-
第2题:
请写出符合以下两个条件的一个函数解析式____________.
①过点(-2,1),②在第二象限内,y随x增大而增大.
正确答案: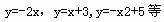
-
第3题:
点M(1,-3,-2)关于y轴的对称点N的坐标是() (A) (1,3,-2) (B) (1,3,2) (C) (-1,3,-2) (D) (-1,-3,2)
B -
第4题:
(2)抛物线y=ax²+bx+c与x轴的两交点的横坐标分别是-1/2,3/2,与y轴交点的纵坐标是-5。
解:设y=a(x-x1)(x-x2) =a(x+1/2)(x-3/2) 与y轴的交点的纵坐标是-5 所以y=20(x+1/2)(x-3/2)/3 化简得y=20x2/3-20x/3-5 -
第5题:
已知x=-1是函数(x)=ax3+bx2的驻点,且曲线y=(x)过点(1,5),求a,b的值.答案:解析:'(x)=3ax2+2bx,'(-1)=3a-2b=0,再由(1)=5得a+b=5,联立解得a=2,b=3.
