抛物线y=ax²+bx+c经过（-1，-22），（0，-8），（2，8）三点，求它的开口方向、对称轴和顶点坐标。

题目

抛物线y=ax²+bx+c经过（-1，-22），（0，-8），（2，8）三点，求它的开口方向、对称轴和顶点坐标。

相似考题

1.已知抛物线y=ax2-1的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为_______。

2.先确定下列抛物线的开口方向、对称轴及顶点，再描点画图：（1） y=-3x²+12x-3（2） y=4x²-24x+26(3)y=2x²+8x-6(4)y=x²/2-2x-1

3.抛物线 y=ax²+bx+c与x轴的公共点是（-1 , 0），（3 , 0），求这条抛物线的对称轴。

4.分别写出抛物线y=4x2与y=-x2/4的开口方向、对称轴及顶点。

更多“抛物线y=ax²+bx+c经过（-1，-22），（0，-8），（2，8）三点，求它的开口方向、对称轴和顶点坐标。”相关问题

  • 第1题：

    下列情形时，如果a＞0，抛物线y=ax²+bx+c的顶点在什么位置？

    （1）方程ax²+bx+c=0有两个不等的实数根；

    （2）方程ax²+bx+c=0有两个相等的实数根；

    （3）方程ax²+bx+c=0无实数根。

     如果a＜0呢？


    ∵a＞0，∴抛物线开口向上。

    （1）∵ax²+bx+c=0有两个不等实根。

            ∴图象与x轴有两个交点。∴顶点在x轴下方。

    （2）∵ax²+bx+c=0有两个相等实根。

             ∴图象与x轴有且只有一个交点。∴顶点在x轴上。

    （3）∵ax²+bx+c=0无实根。

            ∴图象与x轴无交点。∴顶点在x轴上方。

     a0时，（1）顶点在x轴上方;

             （2）顶点在x轴上;

              （3）顶点在x轴下方。


  • 第2题：

    （2）抛物线y=ax²+bx+c与x轴的两交点的横坐标分别是-1/2,3/2,与y轴交点的纵坐标是-5。


    解：设y=a(x-x1)(x-x2) =a(x+1/2)(x-3/2) 与y轴的交点的纵坐标是-5 所以y=20(x+1/2)(x-3/2)/3 化简得y=20x2/3-20x/3-5

  • 第3题：

    如下哪一个问题是解线性方程组

    A．已知系数 a,b,c 求抛物线 y= ax2+bx+c 与x轴的交点坐标。

    B．已知抛物线 y=ax2+bx+c 上三点的坐标，求a,b,c.


    已知抛物线 y=ax2+bx+c 上三点的坐标，求a,b,c.

  • 第4题：

    先确定下列抛物线的开口方向、对称轴及顶点坐标，再描点画图：

    (1) y=x²+2x-3

    (2)y=1+6x-x2

    (3)y=x2/2+2x+1

    (4)y=-x2/4+x-4

  • 第5题：

    已知直线在x轴上的截距为-1，在y轴上的截距为1，又抛物线y=x2+bx+c的顶点坐标为(2，-8)，求直线和抛物线两个交点横坐标的平方和．


    答案：
    解析：

    设直线与抛物线两交点的横坐标为x1和x2，则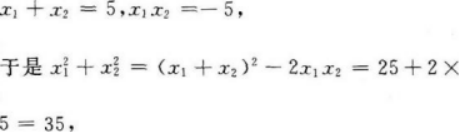

    即直线与抛物线两交点的横坐标的平方和为35．

相关内容