一个多边形的内角和是540°,那么这个多边形的对角线条数是______.
题目
一个多边形的内角和是540°,那么这个多边形的对角线条数是______.
相似考题
更多“一个多边形的内角和是540°,那么这个多边形的对角线条数是______. ”相关问题
-
第1题:
一个多边形的每个外角都等于与它相邻的内角,这个多边形是几边行?能确定它的每个外角的度数吗?
因为外角加其相邻的内角等于180°。
两角相等,则每个角都等于90°。则这个多边形为正方形!!外角都为90°!
-
第2题:
若两个多边形的边数相差1,则它们的内角和、外角和分别有多少异同?
多边形内角和公式:(n-2) ×180°。
多边形外角和:360°
故多边形边数相差1,内角和相差180°
外角和不变,为360°。
-
第3题:
一个多边形有14条对角线,那么这个多边形有( )条边
A.6- B.7- C.8- D.9
正确答案:B
-
第4题:
下面各角能成为某多边形的内角和的是( )
A.430°- B.4343°- C.4320° -D.4360°
正确答案:C
-
第5题:
小明在进行多边形内角和计算时,求得的内角和为1125°,当发现错误之后,重新检查,发现少加了一个内角,问这个内角是多少度,他求的是几边形内角和?
正确答案:
135°、n=9; -
第6题:
“多边形的内角和”是八年级上册的内容,如何引导学生发现和推导出多边形内角和公式是该节课的重点。
(1)如果将让学生体验“数学思考”作为该节课的一项教学目标,那么请列举出该节课涉及的“数学思考”的方法;(10分)
(2)请给出两种引导学生猜想四边形内角和的学生活动设计;(6分)
(3)请给出两种证明四边形内角和的学生活动设计;(6分)
(4)某教师在“多边形的内角和”一节的教学中,设计了如下两个问题:你能说出我们为什么要研究四边形的内角和吗?你能基于四边形内角和的证法,得到五边形、六边形,……,n边形内角和计算公式和证明方法吗?请分析该教师设计这两个问题的意图。(8分)答案:解析:本题主要考查多边形的内角和知识及考生的教学设计能力 -
第7题:
在“多边形内角和”一课上,某教师设计如下的教学过程:
一、学生自主学习,通过阅读课本理解多边形的定义及相关概念
1.多边形的定义:在平面内,由若干条不在同一直线上的线段首尾顺次相连组成的封闭图形叫做多边形。在定义中应注意:①若干条;②首尾顺次相连,二者缺一不可。
2.多边形的分类:有凸多边形和凹多边形之分。
3.多边形的相关概念:边、内角、顶点、对角线、内角和的含义与三角形相同。
4.多边形的命名和表示:通常以边数命名,多边形有n条边就叫做/l,边形。三角形、四边形都属于多边形,其中三角形是边数最少的多边形。多边形的表示方法与三角形、四边形类似。可以用表示它的顶点的字母来表示,可顺时针方向表示,也可逆时针方向表示。
二、探索多边形的内角和的公式(见活动探究卡)
在了解了多边形的有关概念后,我们重点来研究和探索多边形的内角和的公式。
活动探究要求:请以小组为单位,利用活动探究卡与同伴合作探索多边形的内角和。
活动:从多边形的一个顶点引对角线来探索多边形的内角和
边数 从某顶点出发的对角线条数划分成的三角形个数 多边形的内角和 计算规律
3
4
5
6
7
8
结论:④从n边形的一个顶点出发可以引条对角线,把H边形分成个三
角形,每个三角形的内角和 ②n边形的内角和公式: (n>3)(学生讨论、画图、猜想、归纳自己的方法,并请小组的中心发言人在全班进行交流展,教师利用课件演示,师生共同得到结论)
教师小结:在求多边形的内角和时,先把多边形转化成三角形,进而求出内角和.这种由未知转化为已知的方法是我们数学中一种非常重要的方法。
阅读上述教学设计片段,完成下列任务:
(1)本节课的教学目标是什么 (8分)
(2)本节课的教学重难点是什么 (8分)
(3)请为此教学片段设计一个导入过程。(14分)答案:解析:(1)知识与技能:①掌握多边形的概念;②探索并理解多边形的内角和公式;③会用多边形的内角和公式进行计算。
过程与方法:①经历探索多边形内角和公式的过程,提升合情推理意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系;②探索并了解多边形的内角和公式,培养说理和简单推理的意识及能力。
情感、态度与价值观:①经历探索多边形内角和的过程,通过师生共同活动,训练学生的发散性思维.培养学生的创新精神;②进一步发展学生合情推理意识、主动探究习惯,进一步体会数学与现实生活的紧密联系。
(2)教学重点:多边形的内角和公式的探索、归纳及运用公式进行有关计算。
教学难点:如何引导学生参与到探索多边形的内角和公式过程中,通过动手实践、观察分析、归纳总结得出多边形的内角和公式。
(3)导入环节:
工人师傅将一个四边形的桌面用锯子锯掉一个角,剩余的木板会出现什么形状的图形,还剩几个角 内角和是多少
(学生思考、讨论、回答;教师利用课件演示三种情况。得出结论:三角形,四边形,五边形)如何知道五边形的内角和呢
这就是本节课我们需要学习的主要内容:
教师板书课题:4.6探索多边形的内角和(一)
并利用课件展示本节课的学习目标,教师导读,学生理解。 -
第8题:
多边形内角和等于()。
- A、(n-2)×0°;
- B、(n-2)×90°;
- C、(n-2)×180°;
- D、(n-2)×360°。
正确答案:C -
第9题:
用矩形和正多边形命令绘制的矩形和正多边形都是一个单独的对象。
正确答案:正确 -
第10题:
闭合导线的角度闭合差等于该导线构成的多边形的内角和
正确答案:错误 -
第11题:
多选题以下属于拓扑性质的是()A点位于多边形
B两多边形相邻
C线和多边形相交
D多边形的面积
正确答案: C,A解析: 暂无解析 -
第12题:
单选题多边形闭合导线其内角和的理论值为(n-2)×180°,式中的n代表()。A方向数;
B内角数;
C边数;
D观测数。
正确答案: D解析: 暂无解析 -
第13题:
能否存在一个多边形,它的每个外角都等于相邻内角的1/5?简述你的理由。
该多边形为正多边形!
因为外角加其相邻的内角等于180°。
每个外角都等于相邻内角的1/5,则设外角为x度,则内角为5x度。x+5x=6x=180°,则x=30°
根据多边形外角等于360°/n=30°. 故该多边形是正十二边形
-
第14题:
一个凸多边形内角和是1080度,这个多边形的边数是( )
A.5
B.6
C.7
D.8
正确答案:D
根据凸多边形内角和公式180(n一2),其巾n代表边数,求得答案是D。 -
第15题:
一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
正确答案:C
C.点拨:据题意,得(n-2)·180=2×360+180.解得n=7.故选C; -
第16题:
一个多边形的每一个内角都相等,且比它的一个外角大100°,则边数n=_____.
正确答案:
9 -
第17题:
若一个多边形有且仅有两个内角为钝角,有至少两个外角为锐角,问该多边形最多有几条边?A.4
B.5
C.6
D.7答案:B解析:解法一:第一步,本题考查几何问题,属于几何特殊性质类,用代入排除法解题。
第二步,问最多,从最大开始代入。
D选项,如果是7边形,内角和为(7-2)×180°=900°,5个锐角和小于5×90°=450°,加上两个钝角(和小于2×180°=360°)无法达到900°,排除。
C选项,如果是6边形,内角和为(6-2)×180°=720°,4个锐角和小于4×90°=360°,加上两个钝角(和小于2×180°=360°)无法达到720°,排除。
B选项,如果是5边形,内角和为(5-2)×180°=540°,3个锐角和小于3×90°=270°,加上两个钝角(和小于2×180°=360°)可以达到540°,符合题意。
因此,选择B选项。
解法二:第一步,本题考查几何问题,属于几何特殊性质类。
第二步,设各角为A1,A2,……,An,后两个为钝角,其余为锐角。则所有内角加和有90°×2<A1+A2+……+An<(n-2)×90°+180°×2。而多边形内角和为(n-2)×180°,可得180°<(n-2)×180°<(n-2)×90°+360°,化简为2<2n-4<n+2。解得3<n<6。
第三步,n是正整数,只能取4、5,所以这个凸多边形最多是五边形。
因此,选择B选项。 -
第18题:
《多边形的内角和》是八年级上册的内容,如何引导学生发现和推导出多边形内角和公式是该节课的重点。
(1)如果将让学生体验“数学思考”作为该节课的一项教学目标,那么请列出该节课涉及的“数学思考的方法”;
(2)请给出两种引导学生猜想四边形内角和的学生活动设计;
(3)请列出两种证明四边形内角和的学生活动设计;
(4)某教师在《多边形的内角和》一节的教学中,设计了如下两个问题,你能说出我们为什么要研究四边形的内角和吗?你能基于四边形的内角和的证法,得到五边形、六边形,……,n边形内角和计算公式和证明方法吗?请分析该教师设计这两个问题的意图。答案:解析:(1)数学课程标准中关于“数学思考”的其中一条是:在参与观察、实验、猜想、证明、综合实践等数学活动中,发展合情推理和演绎推理能力,清晰地表达自己的想法。而本节课所涉及的“数学思考的方法”是学生在参与四边形、五边形、六边形的内角和的探究过程中,猜想多边形的内角和是(n-2)×180°,然后通过添加辅助线(对角线)等方法证明此结论,并让学生说出自己的探究过程,最后用数学语言表示出多边形的内角和定理:n边形的内角和等于(n-2)×180°。
(2)第一种:
如何利用三角形的内角和求出四边形的内角和,进而发现:只需连接一条对角线,即可将一个四边形分割为两个三角形。学生说出证明过程,教师板书。
追问1:这里连接对角线起到什么作用?
预设:将四边形分割成两个三角形,进而将四边形的内角和问题转化为两个三角形所有内角的和的问题。
追问2:类似地,你能知道五边形、六边形的内角和是多少度吗?
问题:你能从四边形、五边形、六边形的内角和的研究过程获得启发,猜想多边形的内角和与边数的关系(n-2)×180°。
第二种:
提问:前面我们通过从一个顶点出发作对角线,将多边形分割成几个三角形,进而探究出n边形的内角和,那么,是否还有其他分割多边形的方法呢?
学生活动:学生自主探究,小组讨论交流。学生可能会在n边形内任取一点O,连接OA1,OA2,OA3,……,OAn,则n边形被分成了n个三角形,从而才猜想出多边形的内角和是(n×180°-360°)即(n-2)×180°。
(3)方法一:先让学生回忆多边形的对角线的求法:从n边形的一个顶点出发,可以作(n-3)条对角线。它们将n边形分成(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,由于一个三角形的内角和是180°,所以n边形的内角和等于(n-2)×180°。
方法二:前面我们通过从一个顶点出发作对角线,将多边形分割成几个三角形,进而探究出n边形的内角和,那么,是否还有其他分割多边形的方法呢?
学生活动:学生自主探究,小组讨论交流。并让小组代表板演并讲解思路。学生可能有以下几种方法:
如图,在n边形内任取一点O,连接OA1,OA2,OA3,……,OAn,则n边形被分成了n个三角形,这n个三角形的内角和为n×180°,以O为公共顶点的n歌角的和是360°,所以n边形的内角和是(n×180°-360°)即(n-2)×180°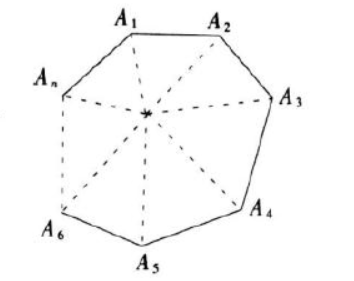
(4)问题一设计意图:采取简单的四边形进行瘾大,利于学生迅速掌握知识,学生利用辅助线多角度的把多边形的内角和灵活地转化成三角形的内角和,体会转化的数学思想,并为下面五边形、六边形以及n边形的内角和做铺垫。
问题二设计意图:引导学生动手操作、动脑思考、小组讨论,从四边形到五边形再到六边形,以知识迁移的方式进一步体会将多边形分割成几个三角形的化归过程。也进一步明确了边数、对角线条数、三角形数对多边形内角和的影响,为从具体的多边形抽象到一般的n边形的内角和的研究奠定基础。 -
第19题:
以下属于拓扑性质的是()
A点位于多边形
B两多边形相邻
C线和多边形相交
D多边形的面积
A,B,C
略 -
第20题:
多边形闭合导线其内角和的理论值为(n-2)×180°,式中的n代表()。
- A、方向数;
- B、内角数;
- C、边数;
- D、观测数。
正确答案:B -
第21题:
闭合导线角度闭合差指的是()
- A、多边形内角观测值之和与理论值之差
- B、多边形内角和理论值与观测值和之差
- C、多边形内角观测值与理论值之差
- D、多边形内角理论值与观测值之差
正确答案:A -
第22题:
判断题闭合导线的角度闭合差等于该导线构成的多边形的内角和A对
B错
正确答案: 对解析: 暂无解析 -
第23题:
单选题在CAD中以下有关多边形的说法错误的是()A多边形是由最少3条至多1024条长度相等的边组成的封闭多段线
B绘制多边形的默认方式是外切多边形
C内接多边形绘制是指定多边形的中心以及从中心点到每个顶角点的距离,整个多边形位于一个虚构的圆中
D外切多边形绘制是指定多边形一条边的起点和端点其边的中点在一个虚构的圆中
正确答案: B解析: 暂无解析
