已知一次函数的图象经过点A（2，1），B（－1，－3）（1）求此一次函数的解析式；（2）求此一次函数的图象与x轴、y轴的交点坐标；（3）求此一次函数的图象与两坐标轴所围成的三角形面积。

题目

已知一次函数的图象经过点A（2，1），B（－1，－3）

（1）求此一次函数的解析式；

（2）求此一次函数的图象与x轴、y轴的交点坐标；

（3）求此一次函数的图象与两坐标轴所围成的三角形面积。

相似考题

1.若反比例函数的图象经过点A(-2,1) ,则它的表达式是 _________________ ．

2.作出函数y=3-2x的图象，根据图象回答下列问题：（1）y的值随着x值增大而__________;（2）图象与x轴的交点坐标是_________________，与y轴的交点坐标是_______________；（3）当x__________时，y＞0 。

3.在同一直角坐标系内一次作出函数y=x+1，y=2x+1，y=3x+1的图象。（1）这几个图象之间有什么差别，又有什么联系？（2）一次函数y=kx+b的一次项系数k对函数的图象有什么影响？

4.已知一次函数y-2x+b的图像经过点（-2，1），则该图像也经过点 （ ）A.（1，7）B.（1，-3）C.（1，5）D.（1，-l）

更多“已知一次函数的图象经过点A(2,1),B(－1,－3)(1)求此一次函数的解析式;(2)求此一次函数的图象与x轴、 ”相关问题

  • 第1题：

    根据二次函数图象上三个点的坐标，求出函数解析式：

    （1）（-1，3）（1，3）（2，6）；     

    （2） （-1，-1）（0，-2）（1，1）；

    （3） （-1，0）（3，0）（1，-5）； 

    （4） （1，2）（3，0）（-2，20）。

  • 第2题：

    用函数的图象求下列方程的解：

    （1）x²-3x+2=0 ;（2）-x²-6x-9=0 ;（3）x²+x+2=0 ; （4）1-x-2x²=0 。

  • 第3题：

    已知函数f(x)=a2+k的图象经过点(1，7)，且其反函数f-1(x)的图像经过点(4，0)，则函数f(x)的表达式是 （ ）

    A．f(x)=4x+3

    B．f(x)=2x+5

    C．f(x)=5x+2

    D．f(x)=3x+5


    正确答案：A

  • 第4题：

    已知m是整数，且一次函数y=(m+4)x+m+2的图象不过第二象限，则m= ；


    正确答案：
    －3或－2   

  • 第5题：

    如图。在直角梯形ABCD中，AB∥CD，∠BAD=90o，且AB=8，AD=3，CD=4，动点P，Q分别以点B和点A为起点同时出发，点P沿B→A，以每秒1个单位速度运动，终点为点A；点Q沿A→D→C→B，以每秒1.5个单位速度运动，终点为点B。设△APQ的面积为y，运动时间为x。
    (1)求y关于x的函数解析式y=f(x)；
    (2)画出函数y=f(x)的图象。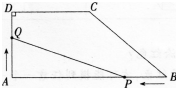


    答案：
    解析：

    (2)函数图象如图所示：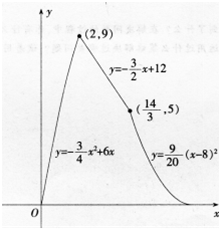

  • 第6题：

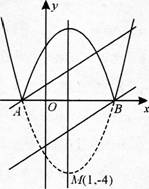
    下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)．
    (1)求出图象与戈轴的交点A，B的坐标；



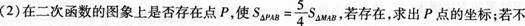
    存在，请说明理由；
    ° (3)将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b(b＜1)与此图象有两个公共点时，b的取值范围．





    答案：
    解析：
    解：(1)由二次函数Y=(x+m)2+k的顶点坐标为M(1，-4)可知，m=-1，k=-4.则二次函数Y=(x-1)2-4与x轴的交点为A(-1，0)，8(3，0).




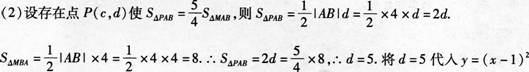
    (3)如图，当直线Y=x+b经过A(-1，0)时-1+b=0，
    可得b=1，又因为b＜1，
    故可知Y=x+b在Y=x+1的下方，
    当直线Y=x+b经过点B(3，0)时，3+b=0，则b=-3，
    由图可知，b的取值范围为-3＜b＜1时，
    直线Y=x+b(b＜1)与此图象有两个公共点.


  • 第7题：

    定义[a，b，c]为函数y=ax2+bc+c的特征数，下面给出特征数为[ 2m ，1-m，-1-m]的函数的一些结论：
    ①当m=-3时，函数图象的顶点坐标是{1/3,-(8/3)}；
    ②当m>0时，函数图象截石轴所得的线段长度大于3/2；
    ③当m<0时，函数在x>1/4时，y随x的增大而减小；
    ④当m≠0时，函数图象经过同一个点。
    其中正确的结论有()。

    A.②③④
    B.①②④
    C.③④
    D.②④

    答案：D
    解析：
    特征数[2m，1-m，-l-m]的函数为y=2mx2+(1-m)x+(-1-m)。①当m=-3时，y=-6x2+4x+

  • 第8题：





    【答辩题目解析】
    1.说一说你对本节课教材的理解。
    2.一次函数图象与x轴交点的意义是什么?


    答案：
    解析：
    1、本节课是在学习了一次函数解析式的基础上，从图象这个角度对一次函数进行近一步的研究。教材先介绍了作函数图象的一般方法：列表、描点、连线法，再进一步总结出作一次函数图象的特殊方法——两点连线法。结合一次函数的图象，教材以议一议的方式，引导学生探索函数解析式与图象二者间的关系，为进一步学习图象及性质奠定了基础。

    2、一次函数图象与x轴的交点可以表示此一次函数在x轴的截距。同时，它也表示当y=0时x的值，同时也能表示y=0时此方程的解。

  • 第9题：

    函数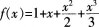的图象与x轴交点的个数是( )。

    A、0
    B、1
    C、2
    D、3

    答案：B
    解析：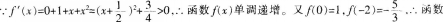
    f(x)的图象与x轴有且只有一个交点。故选B。

  • 第10题：

    关于二次函数y=2-(x+1)2的图象,下列说法正确的是( )。

    A.图象开口向上
    B.图象的对称轴为直线x=1
    C.图象有最低点
    D.图象的顶点坐标(-1，2)

    答案：D
    解析：
    由二次函数图象的性质可知，其开口方向向下，有最大值2，对称轴为x=-1，顶点坐标(-1，2)。二次函数y=a(x+h)2+k(α≠0)中，α决定了二次函数图象的开口方向，顶点坐标为(-h，k)。

  • 第11题：

    已知函数f(x)=x2+4lnx．
    (1)求函数f(x)在[1，e]上的最大值和最小值；
    (2)证明：当x∈[1，+∞)时，函数八戈)的图象在g(x)=2x3的图象的下方。


    答案：
    解析：

  • 第12题：

    填空题
    二次函数y＝－x2＋2x＋n的图象与x轴的一个交点为（3，0），则n＝____．

    正确答案： 3
    解析：
    将（3，0）代人y＝－x2＋2x＋n，得－32＋2×3＋n＝0，解得n＝3．

  • 第13题：

    已知函数 y=x²-4x+3。

    （1）画出函数的图象；

    （2）观察图象，当x取哪些值时，函数值为0？

  • 第14题：

    画出函数 y=x²-2x-3的图象，利用图象回答：

    （1）方程 x²-2x-3=0 的解是什么；

    （2）x取什么值时，函数值大于0 ；

    （3）x取什么值时，函数值小于0 。

  • 第15题：

    11 、点 A （ 2 ， y 1 ） 、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关

    系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ） ．


    正确答案：

    <

    考点：二次函数图象上点的坐标特征。

    分析：本题需先根据已知条件求出二次函数的图象的对称轴，再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系．

    解答：解：∵二次函数y=x2﹣2x+1的图象的对称轴是x=1，

    在对称轴的右面y随x的增大而增大，

    ∵点A（2，y1）、B（3，y2）是二次函数y=x2﹣2x+1的图象上两点，

    23，

    ∴y1y2．

    故答案为：．

    点评：本题主要考查了二次函数图象上点的坐标特征，在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键．

  • 第16题：


    A.常数k＜-1
    B.函数f(x)在定义域范围内，y随着x的增大而减小
    C.若点C(-1，m)，点B(2，n)，在函数f(x)的图象上，则m＜n
    D.函数f(x)图象对称轴的直线方程是y=x

    答案：C
    解析：
    由图象可知常数k＞0，A项错误；当x＞0时，y随着x的增大而减小，当x＜0时，y随着x的增大而减小，B选项说法不严谨，错误；由反比例函数的公式可得，m=-k＜0，



    m＜n，C正确；函数f(x)图象对称轴有两条，y=x和y=-x，D错误。

  • 第17题：

    已知函数f(x)=㏑(x+2)-x2+bx+c，
    (1)若点P(-1，0)在f(x)的图象上，过点P的切线与直线y=-x+2平行，求f(x)的解析式；
    (2)若f(x)在区间[0，2]上单调递增，求b的取值范围。


    答案：
    解析：

  • 第18题：

    已知函数f(x)=（1/2）e2x-ax，g(x)=6xlnx，，h(x)=2e2x-4/x，a>o，b≠0。
    (1)求函数f(x)的最小值；(3分)
    (2)求函数g(x)的单调区间；(3分)
    (3)证明：函数h(x)在[1/2，1]上有且仅有l个零点。(4分)


    答案：
    解析：

  • 第19题：

    已知函数(x)=ax2+b的图像经过点(1，2)且其反函数-1(x)的图像经过点(3，0)，则函数(x)的解析式是( )

    A.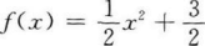
    B.(x)=-x2+3
    C.(x)=3x2+2
    D.(x)=x2+3


    答案：B
    解析：
    【考情点拨】本题主要考查的知识点为反函数的性质． 【应试指导】∵(x)的反函数-1(x)过(3，O)，所以(x)又过点(0，3)所以有(1)=2，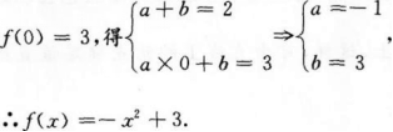

  • 第20题：

    初中数学《二次函数的图象与性质》
    一、考题回顾
    题目来源:5月18日 上午 湖北省黄石市 面试考题
    试讲题目
    1.题目：二次函数的图象与性质
    2.内容：



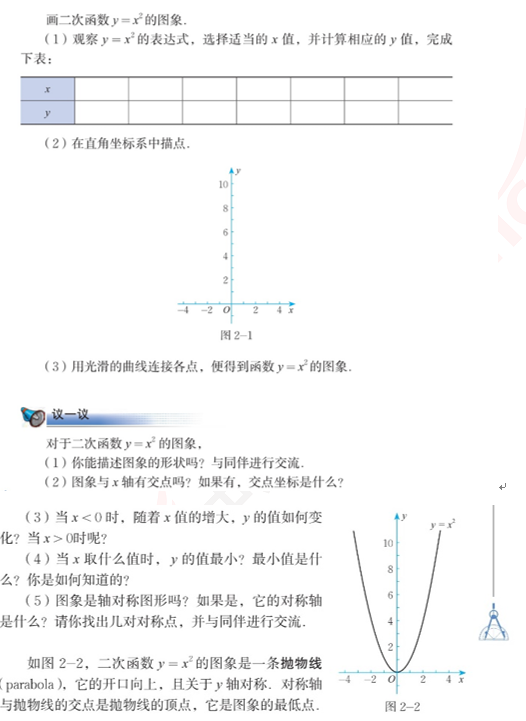
    3.基本要求：
    (1)掌握五点作图法的画图方法，能根据图象理解二次函数的性质;
    (2)试讲十分钟;
    (3)要有合适的板书。
    答辩题目
    1.二次函数 的顶点坐标如何表示?
    2.确定二次函数的表达式需要几个条件?


    答案：
    解析：
    二、考题解析
    【教学过程】
    (一)导入新课
    回顾一次函数和反比例函数，提问：一次函数和反比例函数的图象是什么形状?
    预设：一次函数的图象是一条直线，反比例函数的图象是双曲线。
    追问：二次函数的图象是什么形状的?有什么性质?


    教师资格考试考前黑钻押题，瑞牛题库软件考前更新，下载链接 www.niutk.com

  • 第21题：

    三次函数r=ax3+bx2+cx+d的导函数图象如图1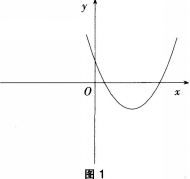， 则此三次函数的图象是( )。
    A．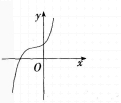
    B．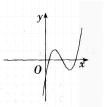
    C．
    D．


    答案：B
    解析：
    若f(x)在某个区间，内有导数，则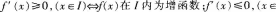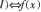在，内为减函数。结合图1中导函数的函数值从左到右依次大于0、小于0、大于0，因此原函数图象从左到右变化趋势依次是单调递增、单调递减、单调递增。因此选B。

  • 第22题：

    一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k<0；②a>0；③当x<3时，y1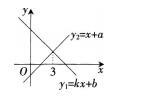

    A.0
    B.1
    C.2
    D.3

    答案：B
    解析：
    由一次函数y1=kx+b的图象可知，该函数在R上单调递减且与y轴的正半轴相交，由此可得k<0，b>0。同理，由一次函数y2=x+a的图象可知，该函数与y轴的负半轴相交，可得a<0。当x<3时，y1=kx+b的图象始终在，y2=x+a图象的上方，所以y1>y2。所以题中结论正确的只有①。

  • 第23题：

    已知一次函数的图像过点（3，5）与（-4，-9），则该函数的图像与y轴交点的坐标为（0，-1）。


    正确答案:正确

相关内容