在直角坐标系Oxyz中，xOz平面上的抛物线z=4x2绕z轴旋转一周所生成的曲面方程为_______

题目

在直角坐标系Oxyz中，xOz平面上的抛物线z=4x2绕z轴旋转一周所生成的曲面方程为_______

相似考题

1.将椭圆绕x轴旋转一周所生成的旋转曲面的方程是:

2.将椭圆绕χ轴旋转一周所生成的旋转曲面的方程是：

3.将xoz坐标面上的双曲线分别绕z轴和x轴旋转一周，则所生成的旋转曲面的方程分别为( )。

4.将双曲线C：绕x轴旋转一周所生成的旋转曲面的方程是（　　）。

更多“在直角坐标系Oxyz中,xOz平面上的抛物线z=4x2绕z轴旋转一周所生成的曲面方程为_______ ”相关问题

  • 第1题：

    旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得？
    A. xOy平面上的双曲线绕x轴旋转所得
    B. xOz平面上的双曲线绕z轴旋转所得
    C. xOy平面上的橢圆绕x轴旋转所得
    D. xOz平面上的椭圆绕x轴旋转所得


    答案：A
    解析：
    提示:利用平面曲线绕坐标轴旋转生成的旋转曲面方程的特点来确定。例如在yOz平面上的曲线f(y,z) = 0,绕y轴旋转所得曲面方程为绕z轴旋转所得曲面方程为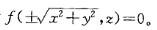

  • 第2题：

    将椭圆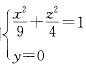，绕x轴旋转一周所生成的旋转曲面的方程是:


    答案：C
    解析：
    提示:利用平面曲线方程和旋转曲面方程的关系直接写出。

  • 第3题：

    将双曲线，绕x轴旋转一周所生成的旋转曲面的方程是（ ）。


    答案：B
    解析：

  • 第4题：

    设直线L过A(1，0，0)，B(0，1，1)两点，将L绕z轴旋转一周得到曲面∑，∑与平面z=0，z=2所围成的立体为Ω.
    　　(Ⅰ)求曲面∑的方程；
    　　(Ⅱ)求Ω的形心坐标.


    答案：
    解析：
    【分析】利用定义求旋转曲面∑的方程；利用三重积分求Ω的形心坐标.

  • 第5题：


    x轴旋转一周，所成旋转曲面记作S。
    (1)在空间直角坐标系下，写出曲面S的方程；
    (2)求曲面S与平面x=0所围成立体的体积。


    答案：
    解析：

相关内容