一枚均匀的硬币连续抛掷3次,求3次均为上面的概率。
题目
一枚均匀的硬币连续抛掷3次,求3次均为上面的概率。
相似考题
更多“一枚均匀的硬币连续抛掷3次,求3次均为上面的概率。 ”相关问题
-
第1题:
通常认为,抛掷一枚质量均匀的硬币的结果是随机的。但实际上,抛掷结果是由抛掷硬币的冲力和初始高度共同决定的。尽管如此,对抛掷硬币的结果作出准确预测还是十分困难。下面哪一项最有助于解释题干所说的现象,即抛掷结果被某些因素决定,但预测却很困难?
A.很长时间以来,抛掷硬币已被用作随机事件的典型例证。
B.如果抛掷一枚质量不均匀的硬币,其结果总能被精确地预测。
C.如果抛掷硬币的初始高度保持稳定不变,则抛掷硬币的结果将仅由抛掷冲力决定。
D.对抛掷硬币结果的准确预测,要求极其精确地估计抛掷硬币的初始高度和冲力。
正确答案:D
解析:题干的结论是:虽然可以确定抛掷结果是由哪些因素决定,但预测结果还是很困难。要解释这个结论必须说明,决定结果的因素很难精确估计,即选项D。 -
第2题:
抛掷一枚硬币出现正面的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次是反面朝上
∵一枚硬币只有正反两面, ∴抛掷一枚硬币,硬币落地后,正面朝上的概率是 1 2 . 故答案为: 1 2 . -
第3题:
3、掷一枚均匀硬币两次,设X为正面向上的次数,求X的概率分布和分布函数。
0;1;2;3 -
第4题:
一枚均匀硬币连续抛掷3次,求3次均为正面向上的概率.答案:解析:3次均为正面向上指第1,2,3次都是正面向上,且它们都是相互独立的.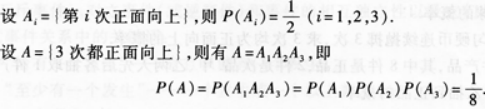
-
第5题:
抛一枚均匀硬币,如果硬币为正面,则掷一颗骰子并记录骰子的点数,如果硬币为反面,则不掷骰子。若进行6次抛掷试验,问骰子出现3点的总次数为3次的概率为多少?
(1)成功抛掷一次的概率是 1 2 × 1 2 = 1 4 . 至少有两次是成功抛掷含三次全都成功抛掷和两次成功抛掷, 其概率P=( 1 4 ) 3 + C 23 ( 1 4 ) 2 ( 3 4 ) = 5 32 . (2)由题设知ε的取值为0,1,2,3,4, p(ε=0)=( 3 4 ) 3 × 1 2 = 27 128 , P(ε=1)=3× 1 4 × 3 4 × 3 4 × 1 2 +( 3 4 ) 3 × 1 2 = 27 64 , P(ε=2)=3× 1 4 ×( 3 4 ) 2 × 1 2 +3× 1 4 × 1 4 × 3 4 × 1 2 = 9 32 , P(ε=3)=( 1 4 ) 3 × 1 2 +3×( 1 4 ) 2 × 3 4 × 1 2 = 5 64 , P(ε=4)=( 1 4 ) 3 × 1 2 = 1 128 . ∴ε的分布列为: ε 0 1 2 3 4 P 7 128 27 64 9 32 5 64 1 128 ∴Eε=0× 7 128 +1× 27 64 +2× 9 32 +3× 5 64 +4× 1 128 = 5 4 .
