多自由度体系自振频率个数与自由度个数相等。 （)

题目

多自由度体系自振频率个数与自由度个数相等。 （)

相似考题

1.一个n个自由度的体系,可以有n+1个自振圆频率。()

2.多自由度体系的振型是反应体系自由振动形状的向量。()此题为判断题(对，错)。

3.如果单自由度体系的阻尼增大,将会使体系的自振周期变短。()此题为判断题(对，错)。

4.多自由度弹性体系的最大地震反应,如果采用直接由各振型最大反应叠加估计体系最大反应,结果会()。A、偏大B、偏小C、相等D、不确定

参考答案和解析
对
更多“多自由度体系自振频率个数与自由度个数相等。 （)”相关问题

  • 第1题：

    自由度(ν)和样品个数(n)的关系正确的是（ ）。


    正确答案：C

  • 第2题：

    图示三种单自由度动力体系自振周期的关系为: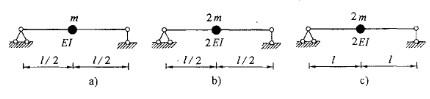

    A. Ta = Tb B. Ta = Tc C. Tb = TcD.都不相等


    答案：A
    解析：
    提示:周期取决于质量与刚度系数之比。

  • 第3题：

    在结构动力计算中，体系振动自由度数n与质点个数m的关系为（）。

    An小于m

    Bm小于n

    C相等

    D不确定


    D
    略

  • 第4题：

    自由度分析就是要确定过程或单元的未知量个数。（）


    正确答案:正确

  • 第5题：

    多自由度体系的自振频率数n1与主振型数n2的大小关系是（）

    • A、n1>n2
    • B、n1
    • C、n1=n1
    • D、不能确定

    正确答案:C

  • 第6题：

    在单因素方差分析中，若因子的水平个数为k，全部观察值的个数为n，那么（）。

    • A、SST的自由度为n
    • B、SSA的自由度为k
    • C、SSE的自由度为n-k-1
    • D、SST的自由度等于SSE的自由度与SSA的自由度之和

    正确答案:C

  • 第7题：

    等直径等厚度的塔式容器的自振周期是将其简化成（）

    • A、单自由度系统
    • B、双自由度系统；
    • C、多自由度系统；
    • D、弹性连续体

    正确答案:D

  • 第8题：

    多自由度系统的固有频率和振型（模态）是如何求得的？


    正确答案: 通过求解无阻尼自由振动方程得到

  • 第9题：

    单自由度体系自由振动的振幅仅取决于体系的：（）

    • A、质量及刚度
    • B、初位移及初速度
    • C、初位移、初速度及质量
    • D、初位移、初速度及自振频率

    正确答案:D

  • 第10题：

    单选题
    自由度等于（）。
    A

    观察值个数减约束条件个数

    B

    n-1

    C

    n-2

    D

    n-k


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    对于多自由度振动体系，下列叙述正确的是（）。
    A

    自振频率和振型取决于干扰力的大小和方向

    B

    自振频率和振型取决于初始位移

    C

    自振频率和振型取决于初始速度

    D

    自振频率和振型取决于结构的质量分布和刚度（柔度）系数


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    等直径等厚度的塔式容器的自振周期是将其简化成（）
    A

    单自由度系统

    B

    双自由度系统；

    C

    多自由度系统；

    D

    弹性连续体


    正确答案： A
    解析： 暂无解析

  • 第13题：

    图示三种单自由度动力体系自振周期的关系为: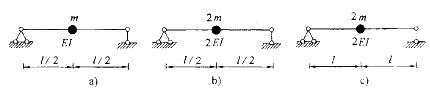


    A. Ta = Tb
    B. Ta = Tc
    C. Tb = Tc
    D.都不相等

    答案：A
    解析：
    提示：周期取决于质量与刚度系数之比。

  • 第14题：

    反应结构动力特性的重要物理参数是（）。

    A振动自由度

    B自振频率

    C振幅

    D初位移


    B
    略

  • 第15题：

    图示单自由度动力体系自振周期的关系为（）

    A（a）=（b）

    B（a）=（c）

    C（b）=（c）

    D都不等


    A
    略

  • 第16题：

    在动力计算中，集中质量的数目与体系自由度数的关系是：（）

    • A、总是相等
    • B、不一定相等
    • C、质点数目总是多于自由度数目
    • D、质点数目总是少于自由度数目

    正确答案:B

  • 第17题：

    在结构动力计算中，体系振动自由度数n与质点个数m的关系为（）。

    • A、n小于m
    • B、m小于n
    • C、相等
    • D、不确定

    正确答案:D

  • 第18题：

    自由度等于（）。

    • A、观察值个数减约束条件个数
    • B、n-1
    • C、n-2
    • D、n-k

    正确答案:A

  • 第19题：

    等直径、等壁厚塔式容器的自振周期是将其简化成（）

    • A、单自由度体系；
    • B、双自由度体系；
    • C、多自由度体系；
    • D、弹性连续体。

    正确答案:D

  • 第20题：

    计算多自由度体系自振频率的方法有（）。

    • A、顶点位移法
    • B、振型分解法
    • C、能量法
    • D、等效质量法
    • E、矩阵迭代法

    正确答案:A,C,D,E

  • 第21题：

    单选题
    等直径、等壁厚塔式容器的自振周期是将其简化成（）
    A

    单自由度体系；

    B

    双自由度体系；

    C

    多自由度体系；

    D

    弹性连续体。


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    在结构动力计算中，体系振动自由度数n与质点个数m的关系为（）。
    A

    n小于m

    B

    m小于n

    C

    相等

    D

    不确定


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    多自由度体系的自振频率数n1与主振型数n2的大小关系是（）
    A

    n1>n2

    B

    n1

    C

    n1=n1

    D

    不能确定


    正确答案： C
    解析： 暂无解析

  • 第24题：

    多选题
    计算多自由度体系自振频率的方法有（）。
    A

    顶点位移法

    B

    振型分解法

    C

    能量法

    D

    等效质量法

    E

    矩阵迭代法


    正确答案： D,B
    解析： 暂无解析

相关内容