哪位数学家证明了在圆柱内嵌一个球，圆柱的体积和球的体积的比是3：2（）A、毕达哥拉斯B、阿基米德C、阿波罗尼奥斯D、托勒密

题目

哪位数学家证明了在圆柱内嵌一个球，圆柱的体积和球的体积的比是3：2（）

  • A、毕达哥拉斯
  • B、阿基米德
  • C、阿波罗尼奥斯
  • D、托勒密
相似考题

1. 两个底面积相等的圆柱，一个高为4.5dm，体积为81dm³。另外一个高为3dm，它的体积是多少？

2.在实际生产中,应用最多最广的冒口形状是圆柱形、球顶圆柱形和腰圆柱形等。()此题为判断题(对，错)。

3.把一个圆柱体削成一个最大的圆锥体，这个圆锥体与原来圆柱体削去部分的体积比是（ ）。A．1：2B．1：3C．2：3D．2：1

4.判断下面的说法是不是正确。（1）圆锥的体积等于圆柱体积的1/3。( ) （2）圆柱的体积大于与等底等高的圆锥的体积。 （ ）（3）圆锥的高是圆柱的高的3倍，它们的体积一定相等。（ ）

更多“哪位数学家证明了在圆柱内嵌一个球，圆柱的体积和球的体积的比是3：”相关问题

  • 第1题：

    如图中的正方形、圆柱和圆锥底面积相等，高也相等，下面哪句话是正确的?( )

    A.圆柱的体积比正方体的体积小一些

    B.圆锥的体积是正方体的1/3

    C.圆柱体积与圆锥体积相等

    D.无答案


    正确答案：B

  • 第2题：

    一个圆柱形容器盛有高度为8厘米的水，放入3个半径与容器底面半径相同的球后，水恰好淹没最上面的球，则单个球与水的体积比为：( )

    A.2：3
    B.1：6
    C.2：1
    D.1：3

    答案：A
    解析：

  • 第3题：

    如果底面直径和高相等的圆柱的侧面积是S,那么圆柱的体积等于（ ）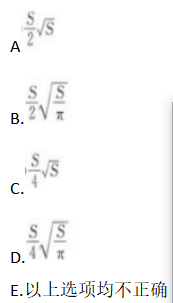


    答案：D
    解析：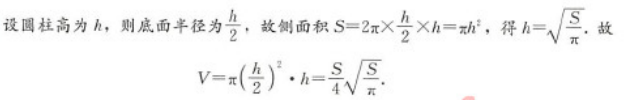

  • 第4题：

    圆锥体体积是相同高度和底面直径圆柱体体积的（）。

    • A、1/2；
    • B、1/3；
    • C、1/4；
    • D、1/5。

    正确答案:B

  • 第5题：

    阿基米德首次计算出来球和外切圆柱体的体积之比为3：2。


    正确答案:错误

  • 第6题：

    发酵罐的公称体积是指（）。

    • A、上下封头体积和罐筒身（圆柱）体积之和
    • B、上封头体积和罐筒身（圆柱）体积之和
    • C、下封头体积和罐筒身（圆柱）体积之和
    • D、罐筒身（圆柱）体积

    正确答案:C

  • 第7题：

    一个圆柱和一个圆锥的底面积和体积分别相等，如果圆锥的高是9厘米，圆柱的高是（）

    • A、3厘米
    • B、9厘米
    • C、27厘米

    正确答案:A

  • 第8题：

    一个圆锥体的底面周长是一个圆柱体底面周长的2倍，这个圆柱的高是这个圆锥高的2倍，这个圆锥体和圆柱体体积的最简单的整数比是（）

    • A、1：2
    • B、3：1
    • C、3：2
    • D、2：3

    正确答案:D

  • 第9题：

    单选题
    一个圆柱体，挖去一个最大的圆锥体，成为一个容器，这个容器的体积是原来圆柱的（）
    A

    1/3

    B

    2/3

    C

    3/3


    正确答案： C
    解析： 暂无解析

  • 第10题：

    判断题
    阿基米德首次计算出来球和外切圆柱体的体积之比为3：2。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第11题：

    单选题
    一个圆柱体和一个圆锥体的底面积相等，圆锥的高是圆柱高的3倍。则圆锥的体积（）圆柱的体积。
    A

    小于

    B

    等于

    C

    大于


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    把一个圆柱体削成一个最大的圆锥体，这个圆锥体与原来圆柱体削去部分的体积比是（）
    A

    1：2

    B

    1：3

    C

    2：3

    D

    2：1


    正确答案： B
    解析： 暂无解析

  • 第13题：

    圆柱度公差带的形状是( )。

    A:一个圆
    B:一个球
    C:两个同心圆
    D:两个同轴圆柱

    答案：D
    解析：
    圆柱度公差带的形状是两个同轴圆柱。

  • 第14题：

    已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是（ ）

    A.6:5
    B.5:4
    C.4:3
    D.3:2
    E.5:2

    答案：D
    解析：

  • 第15题：

    在实际生产中，应用最多最广的冒口形状是圆柱形、球顶圆柱形和腰圆柱形等。


    正确答案:正确

  • 第16题：

    阿基米德测出球的体积和表面积和外切圆柱有2：3的关系。


    正确答案:正确

  • 第17题：

    发酵罐的公称体积是指罐的圆柱体积和上下两个封头体积之和。


    正确答案:错误

  • 第18题：

    把一个圆柱体削成一个最大的圆锥体，这个圆锥体与原来圆柱体削去部分的体积比是（）

    • A、1：2
    • B、1：3
    • C、2：3
    • D、2：1

    正确答案:A

  • 第19题：

    一个圆柱体，挖去一个最大的圆锥体，成为一个容器，这个容器的体积是原来圆柱的（）

    • A、1/3
    • B、2/3
    • C、3/3

    正确答案:B

  • 第20题：

    一个圆柱体和一个圆锥体的底面积相等，圆锥的高是圆柱高的3倍。则圆锥的体积（）圆柱的体积。

    • A、小于
    • B、等于
    • C、大于

    正确答案:B

  • 第21题：

    单选题
    哪位数学家证明了在圆柱内嵌一个球，圆柱的体积和球的体积的比是3：2（）
    A

    毕达哥拉斯

    B

    阿基米德

    C

    阿波罗尼奥斯

    D

    托勒密


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    一个圆柱和一个圆锥的底面积和体积分别相等，如果圆锥的高是9厘米，圆柱的高是（）
    A

    3厘米

    B

    9厘米

    C

    27厘米


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    一个圆锥体的底面周长是一个圆柱体底面周长的2倍，这个圆柱的高是这个圆锥高的2倍，这个圆锥体和圆柱体体积的最简单的整数比是（）
    A

    1：2

    B

    3：1

    C

    3：2

    D

    2：3


    正确答案： C
    解析： 暂无解析

相关内容