单选题当样本含量足够大,总体阳性率与阴性率均不接近0和1,总体率95%可信区间的估计公式为()A P±2.58SxB P±1.96SDC P±1.96SxD P±2.58SpE X±1.96Sp
题目
P±2.58Sx
P±1.96SD
P±1.96Sx
P±2.58Sp
X±1.96Sp
相似考题
更多“单选题当样本含量足够大,总体阳性率与阴性率均不接近0和1,总体率95%可信区间的估计公式为()A P±2.58SxB P±1.96SDC P±1.96SxD P±2.58SpE X±1.96Sp”相关问题
-
第1题:
(2003)n足够大,P不接近于0或1,样本率与总体率比较,统计量u为A.|P-π|/SpB.|P-P|/σSXB(2003)n足够大,P不接近于0或1,样本率与总体率比较,统计量u为
A.|P-π|/Sp
B.|P
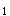 -P
-P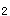 |/σ
|/σ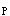
C.|P
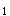 -P
-P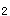 |/S
|/S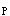
D.|P-π|/σ
E.|P-π|/σ
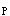 正确答案:E
正确答案:E
-
第2题:
当样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为A.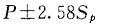
B.
C.
D.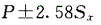
E. 答案:B解析:参考值范围估计用标准差。可信区间的计算用标准误;本题中要求95%可信区间.故排除A、D(2.58是在求99%可信区间时要用到的参数);要通过样本率及样本率的标准误来计算,其中P表示样本率,S
答案:B解析:参考值范围估计用标准差。可信区间的计算用标准误;本题中要求95%可信区间.故排除A、D(2.58是在求99%可信区间时要用到的参数);要通过样本率及样本率的标准误来计算,其中P表示样本率,S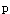 代表样本率的标准误,故本题应选择B。
代表样本率的标准误,故本题应选择B。 -
第3题:
当样本量足够大时,总体阳性率与阴性率均不接近于0和1,总体率95%的可信区间的估计公式为()
A.P±2.58 Sp
B.P±1.96 Sp
C.P±1.96 Sx
D.P±2.58 Sx
E.X±1.96 Sx答案:B解析: -
第4题:
当样本含量足够大,总体阳性率与阴性率均不接近0和1,总体率95%可信区间的估计公式为A.P±2.58S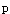
B.P±1.96S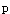
C.P±1.96S
D.P±2.58S
E.X±1.96S 答案:B解析:
答案:B解析: -
第5题:
样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为()
AP±2.58Sp
BP+1.96Sp
CP±1.9Sx
DP±2.58Sx
EP±1.96Sx
B
略 -
第6题:
正态近似法估计总体率的95%可信区间用()。
- A、p±l.96s
- B、p±1.96ς
- C、p±2.58ς
- D、p±1.96sp
正确答案:D -
第7题:
当样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为()
- A、P±2.58Sp
- B、P±1.96Sp
- C、P±1.96Sx
- D、P±2.58Sx
- E、X±1.96Sx
正确答案:B -
第8题:
总体率95%可信区间估计的计算公式为()
- A、p±1.65Sp
- B、p±1.96Sp
- C、p±2.58Sp
- D、p±1.96S
- E、p±2.58S
正确答案:B -
第9题:
当样本含量足够大,总体阳性率与阴性率均不接近0和1,总体率95%可信区间的估计公式为()
- A、P±2.58Sp
- B、P±1.96Sp
- C、P±1.96Sx
- D、P±2.58Sx
- E、X±1.96Sx
正确答案:B -
第10题:
单选题区间P±1.96Sp表示为( )。A大样本总体率90%的可信区间
B大样本总体率95%的可信区间
C小样本总体率95%的可信区间
D小样本总体率90%的可信区间
E大样本总体率99%的可信区间
正确答案: B解析:
当n>100时,可以应用近似正态分布的方法对总体率进行估计,所以总体率95%的可信区间估计为P±1.96Sp。 -
第11题:
单选题当样本量足够大时,总体阳性率与阴性率均不接近于0和1,总体率95%的可信区间的估计公式为( )。AP±2.58Sp
BP±1.96Sp
CP±1.96Sx
DP±2.58Sx
EX±1.96Sx
正确答案: A解析: 暂无解析 -
第12题:
单选题样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为AP±2.58Sp
BP+1.96Sp
CP±1.9Sx
DP±2.58Sx
EP±1.96Sx
正确答案: A解析: 暂无解析 -
第13题:
当样本含量足够大时,样本率又不接近0或1时,以样本率推断总体率95%可信区间的计算公式为A.p+1.645s
B.π±1.96σ
C.p±2.58s
D.X±1.96s
E.p±1.96s 答案:E解析:
答案:E解析: -
第14题:
当样本量足够大时,总体阳性率与阴性率均不接近于0和1,总体率95%的可信区间的估计公式为A.P±2.58S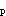
B.P±1.96S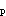
C.P±1.96S
D.P±2.58S
E.X±1.96S 答案:B解析:当样本含量n足够大,阳性率与阴性率均不接近于0和1,样本率的分布近似正态分布,总体率可信区间总体率95%的可信区间:P±1.96S
答案:B解析:当样本含量n足够大,阳性率与阴性率均不接近于0和1,样本率的分布近似正态分布,总体率可信区间总体率95%的可信区间:P±1.96S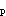 。
。 -
第15题:
样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为A.P±2.58Sp
B.P+1.96Sp
C.P±1.9Sx
D.P±2.58Sx
E.P±1.96Sx答案:B解析: -
第16题:
总体率的可信区间的估计符合下列()情况时,可以用正态近似法处理。
A样本例数n足够大时
B样本率p不太大时
Cnp和n(l-p)大于5时
Dp接近1时
C
略 -
第17题:
当样本含量足够大,总体阳性率与阴性率均不接近0和1,总体率95%可信区间的估计公式为()
AP±2.58Sx
BP±1.96SD
CP±1.96Sx
DP±2.58Sp
EX±1.96Sp
B
略 -
第18题:
总体率的可信区间的估计符合下列()情况时,可以用正态近似法处理。
- A、样本例数n足够大时
- B、样本率p不太大时
- C、np和n(l-p)大于5时
- D、p接近1时
正确答案:C -
第19题:
正太近似法估计总体率95%可信区间用()。
- A、p±1.96s
- B、p±1.96σ
- C、p±2.58σ
- D、p±1.96sp
正确答案:D -
第20题:
当样本含量足够大时,样本率又不接近0或1时,以样本率推断总体率95%可信区间的计算公式为()
- A、p±2.58sP
- B、p+1.645sP
- C、p±1.96sP
- D、π±1.96σπ
- E、X±1.96sX
正确答案:C -
第21题:
单选题对公式p±uαsp的理解,下面错误的是( )。A此公式要求n足够大,p与q均不接近0或1,如np或np均大于5
Bsp是率的标准误,当α取1.96时,求得的范围是总体率的95%可信区间
C只有满足一定的应用条件,p的抽样分布逼近正态分布时,公式才能适用
D求出总体率的95%可信区间后,即可下结论说总体率一定会在此范围内
Ep表示样本阳性率,q=l-p为样本阴性率
正确答案: D解析: 暂无解析 -
第22题:
单选题当样本含量足够大,总体阳性率与阴性率均不接近0和1,总体率95%可信区间的估计公式为()AP±2.58Sp
BP±1.96Sp
CP±1.96Sx
DP±2.58Sx
EX±1.96Sx
正确答案: C解析: 暂无解析 -
第23题:
单选题当样本含量足够大,总体阳性率与阴性率均不接近于0和1,总体率95%可信区间的估计公式为()AP±2.58Sp
BP±1.96Sp
CP±1.96Sx
DP±2.58Sx
EX±1.96Sx
正确答案: B解析: 参考值范围估计用标准差。可信区间的计算用标准误;本题中要求95%可信区间,故排除A,D(2.58是在求99%可信区间时要用到的参数);要通过样本率及样本率的标准误来计算,其中P表示样本率,S代表样本率的标准误,故本题应选择B。
