单选题某班进行一次考试,满分是50分,已知每个人的得分均为整数,则为保证有两个人的得分一样,请问这个班至少有多少人?()A 50B 51C 52D 53
题目
单选题
某班进行一次考试,满分是50分,已知每个人的得分均为整数,则为保证有两个人的得分一样,请问这个班至少有多少人?()
A
50
B
51
C
52
D
53
相似考题
更多“某班进行一次考试,满分是50分,已知每个人的得分均为整数,则为保证有两个人的得分一样,请问这个班至少有多少人?()”相关问题
-
第1题:
在一次竞标中,评标小组对参加竞标的公司进行评分,满分120分。按得分排名,前5名的平均分为115分,且得分是互不相同的整数,则第三名得分至少是:A.112分
B.113分
C.115分
D.116分答案:B解析:设第三名得分为x分,要使x最少,则其他人得分应尽量多,根据题意,第一、二名得分至多为120、119,第四、五名得分至多为x-1、x-2,则,120+119+x+x-1+x-2=115×5,解得x=113。
故正确答案为B。 -
第2题:
某班举行数学测验,试题全部是选择题,共10题,每题1分,得分的部分统计结果如下:
已知,得分至少为3分的,人均2x分;得分最多为7分的,人均x分。这个班级总人数是: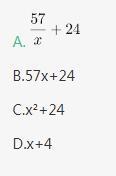 答案:A解析:第一步,本题考查平均数问题,用方程法解题。
答案:A解析:第一步,本题考查平均数问题,用方程法解题。
第二步,设得分至少为3分的人数为y,则全班总分数=2x×y+2×5+1×3=2xy+13①;得分至少为7分的人数为y+5+3+8-2-2-4=y+8,则全班总分数=(y+8)×x+2×10+2×9+4×8=xy+8x+70②。根据①=②,化简可得xy=8x+57,则
因此,选择A选项。 -
第3题:
一次数学考试满分是120分,某班前六名同学的平均得分是114分,排名第六的同学的得分 是108分,假如每人得分是互不相同的整数,那么排名第四的同学最多得多少分?( )
A. 115 B. 116 C. Ill D. 113答案:A解析:要使排名第四的同学得分最高,则需要排名第五的同学得分最低,因此 取第玉名同学的分数为109。设第四名同学的分数为X,要使x最大,不妨设前三名的分数为 x+1,x + 2,x+3,則此时六人分数之和为:r+x+1+x+2+x+3 + 108 + 109 = 4x+223,而六 人分教之和为114X6 = 684,要使x取最大,需要4x+223 -
第4题:
单选题一次数学考试满分为100分,某班前六名同学的平均分为95分,排名第六的同学得86分,假如每个人得分是互不相同的整数,那么排名第三的同学最少得几分?()A94
B97
C95
D96
正确答案: D解析: 暂无解析 -
第5题:
单选题某单位安排职工参加百分制业务知识考试,小周考了88分,还有别外2人的得分比他低。若所有人的得分都是整数,没有人得满分,且任意5人的得分不完全相同,问参加考试的最多有多少人?()A38
B44
C50
D62
正确答案: B解析: 全站数据:本题共被作答1次,正确率为0.00%,易错项为B解析为了让参加考试的人”最多”,则尽可能在每一个分数段都有尽可能多的人分数相同。从88分-99分,共有12个整数分数可以重复,同时又由于”任意5人的得分不完全相同”,所以要求重复的分数的人数最多为4人。这样一共有48人,再加上两个低于88分的人,所以最多50人。故正确答案为C。速解本题与”抽屉原理”的反客为主思想完全相同,逆向思维简化思维量。 -
第6题:
某单位安排职工参加百分制业务知识考试,小周考了 88分,还有另外2人的得分比他低。若所有人的得分都是整数,没有人得满分,且任意5人的得分不完全相同,问参加考试的最多有多少人?()A.38人
B.44人
C.50人
D.62人答案:C解析:最值问题,在88和99分之间一共12个分数,每个分数值都是4人,则共48人,还有2个低于88分的人,共50人,选择C。 -
第7题:
某班级选拔6人参加某学科竞赛,试卷满分为100分,60分及格,6人的平均分为92.5 分。已知所有人得分均为整数且互不相等,那么第三名的成绩最低为( )分。A. 91
B. 93
C. 95
D. 97答案:A解析:要使第三名的成绩最低,那么第一、二名的成绩要尽可能高,第四、五、六名的成绩与第三名应该尽可能的接近,则第一名为100分,第二名为99分。6人的平均分为 92.5分,即6人总成绩为92.5×6 = 555(分),除第一名、第二名外,剩下的四人总成绩为555-100-99 = 356(分),该四人的平均成绩为356 + 4 = 89(分),此时这四人的成绩可能为91、90、88、 87或91、90、89、86。因此第三名的成绩最低为91分。故选A。 -
第8题:
某班级选拔6人参加某学科竞赛,试卷满分为100分,60分及格,6人的平均分为92.5分。已知所有人得分均为整数且互不相等,那么第三名的成绩最低为()分。
- A、91
- B、93
- C、95
- D、97
正确答案:A -
第9题:
单选题某年级共有304人参加新生入学考试,试卷满分为100分,且得分都为整数,总分为15200分,问至少有多少人得分相同?( )A4
B5
C6
D7
正确答案: D解析:
试卷满分为100分,要使得分相同的人尽量少,则分数分布范围应尽量地广。假设极限情况,即有1分,2分,3分,……,100分一百种得分情况,若要使300人中得分相同的人数最少,则每100个人的得分均为1分,2分,3分,……,100分,有3个人得分相同,此时总分为15150分;所以304人中至少有4人得分相同。因此A项正确。
