问答题从0，1，2------9这十个数中不放回随机取4个数能排成4位偶数的概率P1与从中不放回随机取5个数能排成一个5位偶数的概率P2哪个大？

题目
问答题
从0，1，2------9这十个数中不放回随机取4个数能排成4位偶数的概率P1与从中不放回随机取5个数能排成一个5位偶数的概率P2哪个大？
相似考题

1.从1，2，3，……，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于( )。A．0.3024B．0.0302C．0.2561D．0.0285

2.在区间(0, 1)中随机地取两个数, 则两数之差的绝对值小于 的概率为____________．

3.从0,1,2…,9十个数字中随机地、有放回地接连抽取四个数字，则“8”至少出现一次的概率为A、0.1B、0.3439C、0.4D、0.6561

4.从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件概率等于( )。A．0.3024B．0.0302C．0.256lD．0.0285

参考答案和解析
正确答案： P1=P2
解析： 暂无解析
更多“从0，1，2------9这十个数中不放回随机取4个数能排成4位偶数的概率P1与从中不放回随机取5个数能排成一个5位偶数”相关问题

  • 第1题：

    从l、2、3、4、5、6、7、8、9、10这l0个数字中， 任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?( )

    A 1 3

    B．1 4

    C．18

    D．20


    正确答案：A
    15．A【解析】从整体考虑， 分两组和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55， 最接近的两组为27+28，所以共有27—15+1=13个不同的积。

  • 第2题：

    从0，1，2，3，4，5这六个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数的个数为

    (A)300 (B)216 (C) 180 (D)162


    正确答案：C

  • 第3题：

    从0到9这10个数中任取一个数并且记下它的值，放回，再取一个数也记下它的值。当 两个值的和为8时，出现5的概率是多少？


    答案：C
    解析：
    两个数值的和为8,则可能的情况有0+8、1+7、2+6、3+5、4+4、5+3、6+2、7+1、8+0这9种 情况，其中出现5的有2种情况。因此所求概率为2/9

  • 第4题：

    袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X、Y、Z分别表示两次取球所取得的红、黑与白球的个数。①求②求二维随机变量(X,Y)的概率分布。


    答案：
    解析：

  • 第5题：

    袋中有1个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球.以X，Y，Z分别表示两次取球所取得的红球、黑球与白球的个数.
    (Ⅰ)求P{X=1｜Z=0}；
    (Ⅱ)求二维随机变量(X，Y)的概率分布.


    答案：
    解析：

  • 第6题：

    从1,2,…,9这九个数中,随机抽取3个不同的数,这3个数的和为偶数的取法有（ ）种

    A.36
    B.44
    C.60
    D.72
    E.90

    答案：B
    解析：

  • 第7题：

    袋中有l个红色球，2个黑色球与三个白球，现有放回地从袋中取两次，每次取一球，以 X，Y，Z分别表示丽次取球所取得的红球、黑球与白球的个数。
    (1)求P{X=1|Z=0}；
    (2)求二维随机变量(X，Y)的概率分布。


    答案：
    解析：

  • 第8题：

    从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于。

    A.0.3024
    B.0.0302
    C.0.2561
    D.0.0285

    答案：A
    解析：

  • 第9题：

    从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于（）


    正确答案:0.3024

  • 第10题：

    从数字1，2，…，10中有放回地任取4个数字，则数字10恰好出现两次的概率为（）


    正确答案:0.0486

  • 第11题：

    问答题
    从0，1，2------9这十个数中不放回随机取4个数能排成4位偶数的概率P1与从中不放回随机取5个数能排成一个5位偶数的概率P2哪个大？

    正确答案： P1=P2
    解析： 暂无解析

  • 第12题：

    单选题
    从1，2，…，9共九个数字中任取一个数字，取出数字为偶数的概率为(　　)．
    A

    0      

    B

    1      

    C

    5/9     

    D

    4/9


    正确答案： B
    解析： 9个数。偶数的个数是4个

  • 第13题：

    从1、2、3、4、5、6、7、8、9、10这10个数中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不l司的乘积？（ ）

    A．13

    B．14

    C．18

    D．20


    正确答案：A
    从整体考虑分两组，和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55，最接近的两组为27+28，所以共有27-15+1=13个不同的积。

  • 第14题：

    从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件概率等于()。

    A:0.3024
    B:0.0302
    C:0.2561
    D:0.0285

    答案：A
    解析：

  • 第15题：

    从1，2，3，……，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于()。

    A:0.3024
    B:0.0302
    C:0.2561
    D:0.0285

    答案：A
    解析：
    该事件的概率=10*9*8*7*6/105=0.3024。

  • 第16题：

    从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？

    A. 10%
    B. 30%
    C. 60%
    D. 90%

    答案：D
    解析：
    三个数中只要含有1就能满足，共C4,2=6种，三个数中含有2的话，三个数的和必须是偶数，共C3,2-1=2种，不含1和2只有3、4、5能被3整除，因此共有9种满足的情况，总数为c5,3=10，概率为9/10=90%。

  • 第17题：

    从1．2．3．4．5．6．7．8．9这九个数字中，随机取出一个数字，这个数字是奇数的概率是（）


    答案：B
    解析：

  • 第18题：

    从1、2、3、4、5这五个数字中等可能地、有放回地接连抽取两个数字，则这两个数字不相同的概率为()



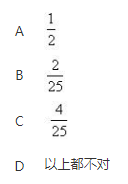    答案：D
    解析：

  • 第19题：

    袋中有l个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球，以X，y，Z分别表示两次取球所取得的红球、黑球与白球的个数。
    (1)求
    (2)求二维随机变量(X，Y)的概率分布。


    答案：
    解析：

  • 第20题：

    在区间（0，1）内随机地取两个数，则所取两数之和不超过5.0概率为（）。


    正确答案:1/8

  • 第21题：

    偶校验码为0时，分组中"1"的个数为（）。

    • A、偶数
    • B、奇数
    • C、随机数
    • D、奇偶交替

    正确答案:A

  • 第22题：

    问答题
    35.从1，2．3，4，5中任取3个数字，则这3个数字中不含1的概率为

    正确答案：
    解析：

  • 第23题：

    单选题
    30.将0，1，2，…，9等10个数字中随机地、有放回地接连抽取4个数字，则“8”至少出现一次的概率为  
    A

    0.1

    B

    0.3439

    C

    0.4

    D

    0.6561


    正确答案： A
    解析：

  • 第24题：

    问答题
    36.从分别标有1．2，…，9号码的9件产品中随机取3件，每次取1件，取后放回，则取得的3件产品的标号都是偶数的概率是

    正确答案：
    解析：

相关内容