单选题三角形全等是三角形面积相等的（　　）．A 充分但不必要条件B 必要但不充分条件C 充要条件D 既不充分也不必要条件

题目
单选题
三角形全等是三角形面积相等的（　　）．
A

充分但不必要条件

B

必要但不充分条件

C

充要条件

D

既不充分也不必要条件

相似考题

1.把一个三角形分成四个面积相等的三角形，可以怎样分？你能想出几种方法？

2.用铁皮剪成两个三角形：（1）如果剪成顶角相等，并且有一条腰相等的两个等腰三角形，则它们全等；（2）如果都有一个角等于42°，且有两边相等，则它们全等；（3） 如果在剪成的⊿ABC和⊿A1B1C1中，∠C＝∠C1＝90°，那么不论是BC＝B1C1，AC＝A1C1，还是BC＝B1C1，AC＝B1C1，剪的两个三角形都全等。 上面说法中，正确的是（ ）。A.（1）B.（1）（2）C.（2）（3）D.（1）（3）

3.若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（ ）。A．20B．24C．12D．6.2 ( ⊙o⊙ )

4.由全等三角形的性质类比出相似三角形的性质是顺向正迁移。()

参考答案和解析
正确答案： B
解析：
如果两个三角形全等，那么这两个三角形面积相等；但是从两个三角形面积相等不能推出这两个三角形全等．所以，三角形全等是三角形面积相等的充分非必要条件．
更多“三角形全等是三角形面积相等的（　　）．”相关问题

  • 第1题：

    叶绿素 对于 （ ） 相当于 （ ） 对于全等三角形

    A．光合作用——对应边相等

    B．化学反应——对应边上的高相等

    C．化学反应——对应中线相等

    D．光合作用——对应角相等


    正确答案：D
    叶绿素是发生光合作用的必要条件，有叶绿素可能发生光合作用，也可能 不发生光合作用，没有叶绿素则必然不会发生光合作用；对应角相等是三角形全等的必要条 件，A项对应边相等是三角形全等的充要条件。故本题正确答案为D。

  • 第2题：

    如图，在长方形ABCD中，已知三角形ABE、三角形ADF与四边形AECF的面积相等，则三角形AEF与三角形CEF的面积之比是


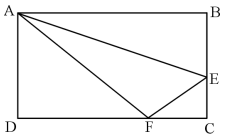    A.5∶1
    B.5∶2
    C.5∶3
    D.2∶1

    答案：A
    解析：
    第一步，三角形ABE、三角形ADF与四边形AECF的面积相等，则三者各占长方形ABCD面积的1/3。连接辅助线AC，则三角形ACD的面积为长方形的1/2。?



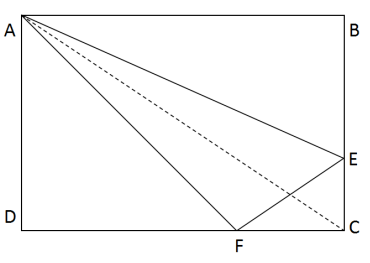
    第二步，三角形ADF与三角形ACD的高相同，都为AD，三角形高相同，底边之比等于面积之比，则FD：CD＝2：3，所以CF＝1/3CD，同理CE＝1/3BC，因此三角形CEF的面积为长方形面积的1/18，则三角形AEF的面积为长方形面积的1/3－1/18＝5/18，所以两者面积之比为5：1。解法二：赋值长方形的长为6，宽为3，则长方形的面积为18。三角形ABE、三角形ADF与四边形AECF的面积相等，则三者的面积各为6。那么FD的长为4，CF长2，则CE的长为1，则三角形CEF的面积为1，三角AEF的面积为6－1＝5，则两者的面积之比为5：1。因此，选择A选项。

  • 第3题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形面积的（ ）。


    答案：B
    解析：
    依题意，一个正三角形和一个正六边形周长相等，所以正三角形的边长为正六边形边长的2倍，正三角形可以划分为4个边长为其一半的全等的小正三角形，正六边形可以划分为边长与其相等的6个全等的小正三角形，所以正六边形的面积为正三角形的1. 5倍。

  • 第4题：

    若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（）。

    A.20
    B.24
    C.12
    D.6.2

    答案：B
    解析：
    两个直角边和为14，直角边中至少有一个大于等于7。根据斜边长度大于任意直角边，可知斜边大于7。则周长大于21。周长与面积相等，直接选B。

  • 第5题：

    不等边三角形的插制方法与步骤基本与等腰三角形一样，知识根据设计需要变动三个骨架枝的长度（）即可。

    • A、长短近似
    • B、互不相等
    • C、完全等同
    • D、大体相等

    正确答案:B

  • 第6题：

    面积相等的图形中下列图形周长最短的是（）

    • A、圆
    • B、三角形
    • C、长方形
    • D、正方形

    正确答案:A

  • 第7题：

    周长相等的等边三角形、正方形、圆形，（）的面积最大。


    正确答案:圆形

  • 第8题：

    甲、乙两个三角形的底相等，乙三角形的高是甲的2.5倍，甲、乙两个三角形的面积比是（）

    • A、2.5：1
    • B、2：5
    • C、5：2

    正确答案:B

  • 第9题：

    单选题
    等底等高的所有三角形面积（）。
    A

    相等

    B

    不相等

    C

    不能确定


    正确答案： A
    解析： 暂无解析

  • 第10题：

    单选题
    下列命题中，正确的个数是（　　）．①等边三角形都相似；②直角三角形都相似；③等腰三角形都相似；④锐角三角形都相似；⑤等腰三角形都全等；⑥有一个角相等的等腰三角形相似；⑦有一个钝角相等的两个等腰三角形相似；⑧全等三角形相似．
    A

    2个

    B

    3个

    C

    4个

    D

    5个


    正确答案： B
    解析：
    等边三角形的三个角都为60°，所以每个等边三角形都相似；直角三角形只有一个角相同，不一定相似；等腰三角形以及锐角三角形都不一定相似，也不一定全等；一个角相等的等腰三角形的三个角都相等，所以一个角相等的等腰三角形相似；全等三角形的每边及每个角相等，当然也相似．

  • 第11题：

    单选题
    一个三角形和一个平行四边形，面积相等，底也相等，那么三角形和平行四边形的高相比较().
    A

    三角形的高是平行四边形的一半

    B

    相等

    C

    三角形的高是平行四边形的2倍


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    甲、乙两个三角形的底相等，乙三角形的高是甲的2.5倍，甲、乙两个三角形的面积比是（）
    A

    2.5：1

    B

    2：5

    C

    5：2


    正确答案： A
    解析： 暂无解析

  • 第13题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：



    答案：B
    解析：
    .［解析］ 本题为几何类题目。因为正三角形和一个正六边形周长相等，又正三角形与正六边形的边的个数比为1:2，所以其边长比为2:1，正六边形可以分成6个小正三角形，边长为1的小正三角形面积：边长为2的小正三角形面积=1:4。所以正六边形面积：正三角形的面积=1×6/4=1.5。所以选B。

  • 第14题：

    用铁皮剪成两个三角形：
    ①如果剪成顶角相等，并且有一条腰相等的两个等腰三角形，则它们全等。
    ②如果都有一个角等于42°，且有两边相等，则它们全等。
    ③如果在剪成的△ABC和△A1B1C1中，∠C=∠C1＝90°，那么不论是BC=B1C1,AC=A1C1，还是BC=B1C1，AC=B1C1，剪的两个三角形都全等。
    上面说法中，正确的是（）。

    A. ①
    B. ①②
    C. ②③
    D. ①③

    答案：D
    解析：
    ［解析］ 根据三角形角边角规则，①③正确，②错误。

  • 第15题：

    如图，由四个全等的直角三角形拼成一个大正方形，每个三角形的面积都是1，且两直角边之比大于等于2，则这个大正方形的面积至少是()。

    A.4
    B.5
    C.6
    D.7

    答案：B
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，根据图形可知大正方形面积＝4个三角形面积＋小正方形面积＝4＋小正方形面积，小正方形边长＝三角形长直角边－短直角边，那么当三角形两直角边差最小时，可得大正方形面积最小，由于两直角边之比大于等于2，即当两直角边之比等于2时，大正方形面积最小。
    第三步，设三角形短直角边为a，则长直角边为2a，三角形的面积为

    解得a＝1，所以小正方形的面积为（2a－a）2＝1×1＝1，故大正方形面积至少为4＋1＝5。
    因此，选择B选项。

  • 第16题：

    分角线投照技术的基本设计原理是根据共边三角形内若有两个角相等，则

    A．这两个三角形垂直原理
    B．这两个三角形相似原理
    C．这两个三角形平行原理
    D．这两个三角形全等原理
    E．以上都不对

    答案：D
    解析：

  • 第17题：

    周长相等的等边三角形、正方形、圆形，哪一个的面积最大？


    正确答案: 圆形

  • 第18题：

    由驴桥定理可判断的是（）。

    • A、等边三角形三个角相等
    • B、等边三角形角度与边长的关系
    • C、等腰三角形两底角相等
    • D、等腰三角形底角与腰长的关系

    正确答案:C

  • 第19题：

    下面关于“等腰三角形”的定义，（）说法最为恰当。

    • A、两腰相等的三角形叫做等腰三角形
    • B、有两边相等的三角形是等腰三角形

    正确答案:B

  • 第20题：

    等底等高的所有三角形面积（）。

    • A、相等
    • B、不相等
    • C、不能确定

    正确答案:A

  • 第21题：

    单选题
    下面关于“等腰三角形”的定义，（）说法最为恰当。
    A

    两腰相等的三角形叫做等腰三角形

    B

    有两边相等的三角形是等腰三角形


    正确答案： B
    解析： 暂无解析

  • 第22题：

    多选题
    在销售量不变的情况下，如果保本点降低，则（）。
    A

    盈利区的三角形面积有所扩大

    B

    盈利区的三角形面积有所缩小

    C

    亏损区的三角形面积有所扩大

    D

    亏损区的三角形面积有所缩小

    E

    盈利与亏损区的三角形面积都不变


    正确答案： E,D
    解析： 暂无解析

  • 第23题：

    填空题
    周长相等的等边三角形、正方形、圆形，（）的面积最大。

    正确答案： 圆形
    解析： 暂无解析

  • 第24题：

    单选题
    三角形全等是三角形面积相等的（　　）．
    A

    充分但不必要条件

    B

    必要但不充分条件

    C

    充要条件

    D

    既不充分也不必要条件


    正确答案： A
    解析：
    如果两个三角形全等，那么这两个三角形面积相等．但是从两个三角形面积相等不能推出这两个三角形全等．所以，三角形全等是三角形面积相等的充分非必要条件．

相关内容