单选题在区间（－∞，＋∞）内方程|x|1/4＋|x|1/2－cosx＝0（　　）。A 无实根B 有且仅有一个实根C 至少有两个实根D 有无穷多个实根

题目
单选题
在区间（－∞，＋∞）内方程|x|1/4＋|x|1/2－cosx＝0（　　）。
A

无实根

B

有且仅有一个实根

C

至少有两个实根

D

有无穷多个实根

相似考题

1.设有方程f(x)=0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分法求该方程在区间[a，b]上的一个实根，采用的算法设计技术为（ ）

2.方程x3＋2x2－x－2＝0在[－3，2]内（）A.有1个实根 B.有2个实根 C.至少有1个实根 D.无实根

3. (1)F’(x)>0； (2)F’(x)=0在[a，b]内有唯一实根．

4.设有方程f(x)一0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分化法求该方程在区间[a’b]上的一个实根，采用的算法设计技术为

参考答案和解析
正确答案： B
解析：
设f（x）＝|x|1/4＋|x|1/2－cosx，因为|cosx|≤1，则当x→＋∞时，f（x）→＋∞；同理当x→－∞时，f（x）→＋∞；又f（0）＝－1＜0，f（x）连续，由介值定理知f（x）＝0在（0，＋∞）内至少存在一个实根，同理，f（x）＝0在（－∞，0）内至少存在一个实根。综上，知f（x）＝0在（－∞，＋∞）内至少存在两个实根。D项，由上面的分析及函数的连续性，知实根的个数不是无限的。
更多“单选题在区间（－∞，＋∞）内方程|x|1/4＋|x|1/2－cosx＝0（　　）。A 无实根B 有且仅有一个实根C 至少有两个实根D 有无穷多个实根”相关问题

  • 第1题：

    关于x的方程2cos2x-sinx+a0在区间[0，7π/6]上恰好有两个不等实根，则实数a的取值范围是_____。


    答案：
    解析：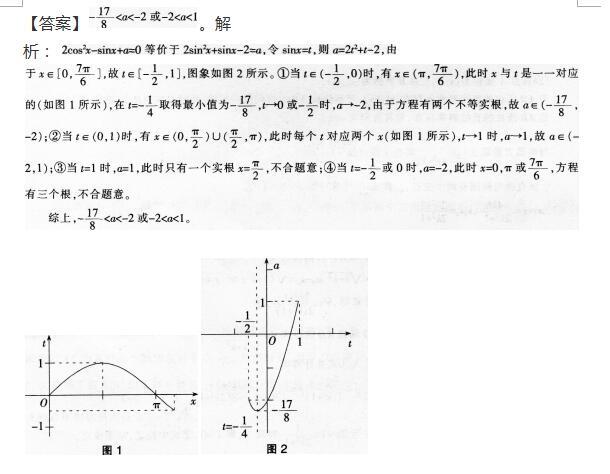

  • 第2题：

    设函数f(x)在区间［0，1］上具有2阶导数，且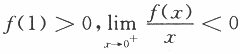，证明：
    　　(Ⅰ)方程f(x)=0在区间(0，1)内至少存在一个实根；
    　　(Ⅱ)方程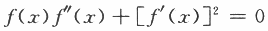在区间(0，1)内至少存在两个不同实根.


    答案：
    解析：

  • 第3题：

    a,b,c是一个三角形的三边长,则方程x2+2（a+b）x+c2=0的根的情况为

    A.有两个不等实根
    B.有两个相等实根
    C.只有一个实根
    D.没有实根
    E.无法断定

    答案：A
    解析：

  • 第4题：

    设随机变量X～U［1,7］,则方程x^2+2Xx+9=0有实根的概率为().



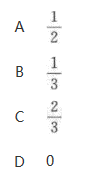    答案：C
    解析：
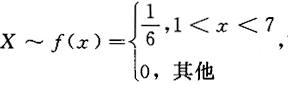    ，方程x^2+2Xx+9=0有实根的充要条件为.

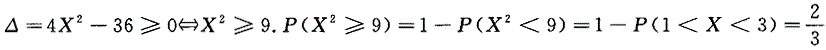
  • 第5题：

    方程x-cos(x-1)=0在下列区间中至少有一个实根的区间是( ).

    A.(-∞，0)
    B.(0，π)
    C.(π，4)
    D.(4，+∞)

    答案：B
    解析：
    记f(x)=x-cos(x-1)，则f(0)=-2＜0，f(π)=π＞0，又f(x)在[0，π]上连续，由零点定理知，应选B.

  • 第6题：


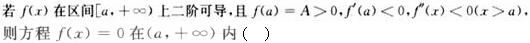    A.没有实根
    B.有两个实根
    C.有无穷多个实根
    D.有且仅有一个实根

    答案：D
    解析：

  • 第7题：

    方程x-lnx-2=0在区间（0，+∞）内（ ）。《》（ ）

    A.没有实根
    B.只有一个实根
    C.有两个相异的实根
    D.有两个以上相异实根

    答案：C
    解析：

  • 第8题：

    若a，b是方程f（x）=0的两个相异的实根，f（x）在［a，b］上连续，且在（a，b）内可导，则方程f’（x）=0在（a，b）内（）．

    • A、只有一个根
    • B、至少有一个根
    • C、没有根
    • D、以上结论都不对

    正确答案:B

  • 第9题：

    设随机变量X服从正态分布U（μ，σ2）（σ>0），且二次方程y2+4y+X=0无实根的概率为1/2，则μ=（）


    正确答案:4

  • 第10题：

    单选题
    方程x5-3x=1在下列区间内至少有一个实根的区间是（）．
    A

    （0，1）

    B

    （1，2）

    C

    （2，3）

    D

    （3，+∞）


    正确答案： B
    解析： 暂无解析

  • 第11题：

    单选题
    方程x-cosx-1=0在下列区间中至少有一个实根的区间是（）．
    A

    （-≥，0）

    B

    （0，π）

    C

    （π，4）

    D

    （4，+∞）


    正确答案： D
    解析： 暂无解析

  • 第12题：

    问答题
    已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。

    正确答案： 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
    （1）若p为真，则q为假。
    p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
    q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
    取交集得到，m≥3：
    （2）若q为真，则p为假。
    q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
    取交集得到：1综上所述m≥3或1
    解析： 暂无解析

  • 第13题：

    设随机变量X～N（μ,σ^2）,且方程x^2+4r+X=0无实根的概率为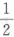,则μ=_______.


    答案：1、4
    解析：
    因为方程x^2+4x+X=0无实根，所以16-4X小于0，即X>4.由X～N（μ，σ）且P(X>4)=1/2 得μ=4

  • 第14题：


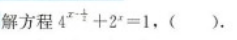    A.方程有两个正实根
    B.方程只有一个正实根
    C.方程只有一个负实根
    D.方程有一正一负两个实根
    E.方程有两个负实根

    答案：C
    解析：

  • 第15题：

    设f（x）=x（x-1）（x-2），则方程



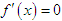
    的实根个数是（　　）。

    A、 3
    B、 2
    C、 1
    D、 0

    答案：B
    解析：
    先对方程求导，得：



    再根据二元函数的判别式



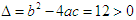
    判断可知方程有两个实根。

  • 第16题：


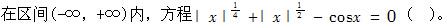    A.无实根
    B.有且仅有一个实根
    C.有且仅有两个实根
    D.有无穷多个实根

    答案：C
    解析：

  • 第17题：

    若a，6是方程f(x)=0的两个相异的实根，f(x)在[a，b]上连续，且在(a，b)内可导，则方程f´(x)=0在(a，b)内( ).

    A.只有一个根
    B.至少有一个根
    C.没有根
    D.以上结论都不对

    答案：B
    解析：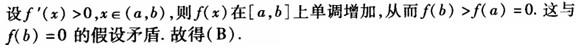

  • 第18题：


    A.无实根
    B.有唯一实根
    C.有三个不同实根
    D.有五个不同实根

    答案：B
    解析：

  • 第19题：

    已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。


    正确答案: 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
    （1）若p为真，则q为假。
    p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
    q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
    取交集得到，m≥3：
    （2）若q为真，则p为假。
    q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
    取交集得到：1综上所述m≥3或1

  • 第20题：

    方程x5-3x=1在下列区间内至少有一个实根的区间是（）．

    • A、（0，1）
    • B、（1，2）
    • C、（2，3）
    • D、（3，+∞）

    正确答案:B

  • 第21题：

    单选题
    在区间（－∞，＋∞）内方程|x|1/4＋|x|1/2－cosx＝0（　　）。
    A

    无实根

    B

    有且仅有一个实根

    C

    至少有两个实根

    D

    有无穷多个实根


    正确答案： A
    解析：
    设f（x）＝|x|1/4＋|x|1/2－cosx，因为|cosx|≤1，则当x→＋∞时，f（x）→＋∞；同理当x→－∞时，f（x）→＋∞；又f（0）＝－1＜0，f（x）连续，由介值定理知f（x）＝0在（0，＋∞）内至少存在一个实根，同理，f（x）＝0在（－∞，0）内至少存在一个实根。综上，知f（x）＝0在（－∞，＋∞）内至少存在两个实根。D项，由上面的分析及函数的连续性，知实根的个数不是无限的。

  • 第22题：

    单选题
    若a，b是方程f（x）=0的两个相异的实根，f（x）在［a，b］上连续，且在（a，b）内可导，则方程f’（x）=0在（a，b）内（）．
    A

    只有一个根

    B

    至少有一个根

    C

    没有根

    D

    以上结论都不对


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    若f（x）在区间[a，＋∞）上二阶可导，且f（a）＝A＞0，f′（a）＜0，f″（x）＜0（x＞a），则方程f（x）＝0在（a，＋∞）内（　　）。
    A

    没有实根

    B

    有两个实根

    C

    有无穷多个实根

    D

    有且仅有一个实根


    正确答案： D
    解析：
    由f″（x）＜0（x＞a）知f′（x）单调减少，又f′（a）＜0，则f′（x）在区间（a，＋∞）上恒小于0，即f（x）在区间（a，＋∞）上单调减少，又由f（a）＝A＞0，且f（x）在区间[a，＋∞）上二阶可导，故方程f（x）＝0在（a，＋∞）内有且仅有一个实根。

  • 第24题：

    单选题
    设f(x)=x(x-1)（x-2），则方程f'(x)=0的实根个数是：
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： A
    解析：

相关内容