单选题微分方程y″－4y′＋5y＝0的通解为（　　）。A ex（C1cos2x＋C2sin2x）B C1e－x＋C2e5xC e2x（C1cosx＋C2sinx）D C1ex＋Ce－5x

题目

单选题

微分方程y″－4y′＋5y＝0的通解为（　　）。

e^x（C₁cos2x＋C₂sin2x）

C₁e^－^x＋C₂e^5x

e^2x（C₁cosx＋C₂sinx）

C₁e^x＋Ce^－^5x

相似考题

1.求微分方程y″+4y′= 2ex的通解．（6分）

2.微分方程y''+2y=0的通解是：(A,B为任意常数）

3.方程y"-2y'+5y=0的通解为( )。A y=ex(c1cosx+c2sinx) B y=e-x(c1cos2x+c2sin2x) C y=ex(c1cos2x+c2sin2x) D y=e-x(c1cosx+c2sinx)

4.求微分方程ex-ydx-dy=0的通解.

更多“单选题微分方程y″－4y′＋5y＝0的通解为（　　）。A ex（C1cos2x＋C2sin2x）B C1e－x＋C2e5xC e2x（C1cosx＋C2sinx）D C1ex＋Ce－5x”相关问题

第1题：

在下列微分方程中，以函数y＝C1e^－x＋C2e^4x（C1，C2为任意常数）为通解的微分方程是（　　）。

A． y″＋3y′－4y＝0
B． y″－3y′－4y＝0
C． y″＋3y′＋4y＝0
D． y″＋y′－4y＝0

答案：B
解析：

由题意知，二阶常系数齐次线性微分方程的特征方程的两个根为－1和4，只有B项满足。
【总结】求二阶常系数齐次线性微分方程y″＋py′＋qy＝0的通解的步骤：
①写出微分方程的特征方程r2＋pr＋q＝0；
②求出特征方程的两个根r1，r2；
③根据r1，r2的不同情形，写出微分方程的通解：
a．当r1≠r2，

b．当r1＝r2，

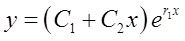
c．一对共轭复根r1，2＝α±βi，y＝eαx（C1cosβx＋C2sinβx）。
第2题：

微分方程y′+y=0的通解为（）.《》（）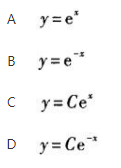

答案：D
解析：
第3题：

微分方程y'＋x=0的通解为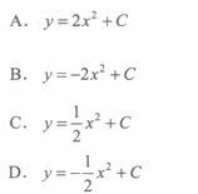

答案：D
解析：
[解析]所给方程为可分离变量方程．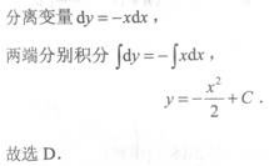
第4题：

微分方程y′′+6y′+13y=0的通解为.

答案：
解析：
【答案】
【考情点拨】本题考查了二阶线性齐次微分方程的通解的知识点.
【应试指导】微分方程y''+6y'+13y=0的特征方程
第5题：

微分方程y′-2xy=0的通解为y=_____.

答案：
解析：
所给方程为可分离变量方程．
第6题：

下列结论不正确的是（）。
- A、y"+y=e^x的一个特解的待定形式为y^*=Ae^x
- B、y"+y=sinx的一个特解的待定形式为y^*=x（c₁cosx+c₂sinx）
- C、y"-4y’+4y=e^2x的一个特解的待定形式为y^*=Axe^2x
- D、D.y"-4y’+4y=x²的一个特解的待定形式为y^*-（Ax²+Bx+x
正确答案:D
第7题：

填空题
微分方程y″＋[2/（1－y）]（y′）2＝0的通解为____。

正确答案： y=1-1/(c₁x+c₂)
解析：
原微分方程为y″＋[2/（1－y）]（y′）²＝0，令y′＝p，则y″＝pdp/dy，原方程变形为pdp/dy＋2p²/（1－y）＝0，即p[dp/dy＋2p/（1－y）]＝0。如果p＝0，则y＝c，这不是此方程的通解。如果p≠0，则有dp/dy＝2p/（y－1），分离变量并积分得ln|p|＝2ln|y－1|＋ln|c|，p＝c₁（y－1）² 即 dy/dx＝c₁（y－1）²故∫dy/（y－1）²＝∫c₁dx⇒－1/（y－1）＝c₁x＋c₂⇒y＝1－1/（c₁x＋c₂）。
第8题：

填空题
若二阶常系数线性齐次微分方程y″＋ay′＋by＝0的通解为y＝（C1＋C2x）ex，则非齐次方程y″＋ay′＋by＝x满足条件y（0）＝2，y′（0）＝0的解为y＝____。

正确答案： -xe^x+x+2
解析：
由题意可知，r＝1是已知齐次方程对应的特征方程的二重根，则该特征方程为（r－1）²＝r²－2r＋1＝0，齐次方程为y″－2y′＋y＝0设y^*＝Ax＋B为已知非齐次方程y″－2y′＋y＝x的特解，代入y″－2y′＋y＝x得0－2A＋Ax＋B＝x，则A＝1，B＝2A＝2。故已知非齐次方程的通解为y＝（C₁＋C₂x）e^x＋x＋2。又y（0）＝2，y′（0）＝0，代入以上通解得C₁＝0，C₂＝－1。故所求方程特解为y＝－xe^x＋x＋2。
第9题：

单选题
在下列微分方程中，以y＝C1ex＋C2cos2x＋C3sin2x（C1，C2，C3为任意常数）为通解的是（　　）。
A
y‴＋y″－4y′－4y＝0
B
y‴＋y″＋4y′＋4y＝0
C
y‴－y″－4y′＋4y＝0
D
y‴－y″＋4y′－4y＝0

正确答案： D
解析：
根据题设中通解的形式可知，所求齐次方程中对应的特征根为r₁＝1，r₂_，₃＝±2i。故特征方程为（r－1）（r－2i）（r＋2i）＝0即r³－r²＋4r－4＝0，则所求微分方程为y‴－y″＋4y′－4y＝0。
第10题：

填空题
y″－4y＝e2x的通解为____。

正确答案： y=C₁e^-^2x+(C₂+x/4)e^2x(其中C₁,C₂为任意常数)
解析：
原方程为y″－4y＝e^2x，其齐次方程对应的特征方程为r²－4＝0，解得r₁_，₂＝±2，故其对应的齐次方程y″－4y＝0的通解为y₁＝C₁e^－^2x＋C₂e^2x。因为非齐次方程右端的非齐次项为e^2x，2为特征方程的单根，故原方程特解可设为y^*＝Axe^2x，代入原方程得A＝1/4，故原方程的通解为y＝y₁＋y^*＝C₁e^－^2x＋C₂e^2x＋xe^2x/4。
第11题：

单选题
微分方程y″－4y′＋5y＝0的通解为（　　）。
A
e^x（C₁cos2x＋C₂sin2x）
B
C₁e^－^x＋C₂e^5x
C
e^2x（C₁cosx＋C₂sinx）
D
C₁e^x＋Ce^－^5x

正确答案： B
解析：
原微分方程为齐次方程，其对应的特征方程为r²－4r＋5＝0，解得r＝2±i。故方程通解为y＝e^2x（C₁cosx＋C₂sinx）。
第12题：

单选题
微分方程y″－2y′＋2y＝ex的通解为（　　）。
A
y＝e^x（c₁cosx－c₂sinx）＋e^x
B
y＝e^x（c₁cos2x－c₂sin2x）＋e
C
y＝e^x（c₁cosx＋c₂sinx）＋e^x
D
y＝e^x（c₁cos2x＋c₂sin2x）＋e^x

正确答案： B
解析：
原微分方程为y″－2y′＋2y＝e^x，其对应的齐次方程为y″－2y′＋2y＝0，该齐次方程的特征方程为r²－2r＋2＝0，解得r₁_，₂＝1±i。故原方程对应的齐次方程的通解为y(＿)＝e^x（c₁cosx＋c₂sinx）。设y^*＝Ae^x为原方程的特解，将其代入原方程可解得A＝1。故原方程的通解为y＝e^x（c₁cosx＋c₂sinx）＋e^x。
第13题：

微分方程xy'-ylny=0的通解为( )。

A、y=cex
B、y=clnx
C、y=lncx
D、y=ecx

答案：D
解析：
方程是可分离变量的方程，可化为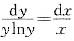，两边积分得lnlny=lnx+lnc，即其通为y=ecx
第14题：

微分方程y''-4y=4的通解是（）（C1,C2为任意常数)。

答案：B
解析：
提示：显然C不是通解；对应齐次方程的通解为C1e2x+C2e-2x ,y=-1是一个特解，故应选B。
第15题：

微分方程y′-y=0的通解为()．

A.y=ex+C
B.y=e-x+C
C.y=Cex
D.y=Ce-x

答案：C
解析：
所给方程为可分离变量方程．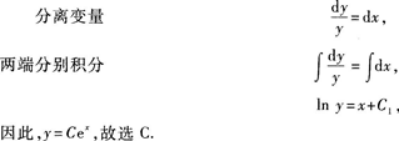
第16题：

微分方程y''+y=0的通解是 .

答案：
解析：
【考情点拨】本题考查了二阶线性微分方程的通解知识点.【应试指导】微分方程y''+y=0的特征方程是r2+1=0.
第17题：

二阶常系数齐次微分方程y″-4y′+4y=0的通解为_____．

答案：
解析：
第18题：

单选题
以y1＝ex，y2＝e2xcosx为特解的最低阶数的常系数线性齐次方程为（　　）。
A
y‴－5y″－9y′－5y＝0
B
y‴－5y″－5y′－5y＝0
C
y‴－5y″＋9y′－5y＝0
D
y‴－5y″＋5y′－5y＝0

正确答案： A
解析：
由题意可知，r₁＝1，r₂_，₃＝2±i是其特征方程的根，则最低的齐次方程的阶数为3，则其特征方程为（r－1）（r－2－i）（r－2＋i）＝0，即（r－1）（r²－4r＋5）＝0，r³－5r²＋9r－5＝0。故满足题意的齐次方程为y‴－5y″＋9y′－5y＝0。
第19题：

单选题
以y1＝ex，y2＝e2xcosx为特解的最低阶数的常系数线性齐次方程为（　　）。
A
y‴＋5y″＋9y′＋5y＝0
B
y‴＋5y″＋9y′－5y＝0
C
y‴－5y″＋9y′＋5y＝0
D
y‴－5y″＋9y′－5y＝0

正确答案： C
解析：
由题意可知，r₁＝1，r₂_，3＝2±i是其特征方程的根，则最低的齐次方程的阶数为3，则其特征方程为（r－1）（r－2－i）（r－2＋i）＝0，即（r－1）（r²－4r＋5）＝0，r³－5r²＋9r－5＝0。故满足题意的齐次方程为y‴－5y″＋9y′－5y＝0。
第20题：

填空题
微分方程y″－2y′＋2y＝ex的通解为____。

正确答案： y=e^x(c₁cosx+c₂sinx)+e^x
解析：
原微分方程为y″－2y′＋2y＝e^x，其对应的齐次方程为y″－2y′＋2y＝0，该齐次方程的特征方程为r²－2r＋2＝0，解得r₁_，₂＝1±i。故原方程对应的齐次方程的通解为y(＿)＝e^x（c₁cosx＋c₂sinx）。设y^*＝Ae^x为原方程的特解，将其代入原方程可解得A＝1。故原方程的通解为y＝e^x（c₁cosx＋c₂sinx）＋e^x。
第21题：

单选题
下列结论不正确的是（）。
A
y+y=e^x的一个特解的待定形式为y^*=Ae^x
B
y+y=sinx的一个特解的待定形式为y^*=x（c₁cosx+c₂sinx）
C
y-4y’+4y=e^2x的一个特解的待定形式为y^*=Axe^2x
D
D.y-4y’+4y=x²的一个特解的待定形式为y^*-（Ax²+Bx+x

正确答案： A
解析： y"+y=0的特征根为λ=±i，故（A）、（B）的特解的形式均正确，y"-4y’+4y=0的特征方程为λ²-4λ+4=0，（λ-2）²=0，有一个二重根λ^1,2=2，故（C）的特解的形式正确，而（D）不正确。
第22题：

单选题
微分方程（ex＋y＋ex）dx＋（ex＋y－ey）dy＝0的通解是（　　）。
A
（1－e^x）（1＋e^y）＝C
B
（1＋e^x）（1－e^y）＝C
C
e^y＝C（1－e^x）－1
D
e^y＝1－C（1＋e^x）

正确答案： B
解析：
∫（e^x^＋^y＋e^x）dx＝e^x^＋^y＋e^x＋f（y），∫（e^x^＋^y－e^y）dy＝e^x^＋^y－e^y＋g（x），故f（y）＝－e^y，g（x）＝e^x。（e^x^＋^y＋e^x）dx＋（e^x^＋^y－e^y）dy＝d（e^x^＋^y＋e^x－e^y＋C）。
第23题：

单选题
微分方程xdy－ydx＝y2eydy的通解为（　　）。
A
y＝x（e^x＋C）
B
x＝y（e^y＋C）
C
y＝x（C－e^x）
D
x＝y（C－e^y）

正确答案： C
解析：
原微分方程xdy－ydx＝y²e^ydy，变形可得（xdy－ydx）/y²＝e^ydy，即－d（x/y）＝d（e^y），积分得－x/y＝e^y－C。即x＝y（C－e^y）就是微分方程的通解。
第24题：

单选题
微分方程y″－2y′＋2y＝ex的通解为（　　）。
A
y＝e^x（c₁cosx＋c₂sinx）＋e^x
B
y＝e^x（c₁cosx＋c₂sinx）－e^x
C
y＝e^x（c₁cosx－c₂sinx）＋e^x
D
y＝e^x（c₁cosx－c₂sinx）－e^x

正确答案： D
解析：
原微分方程为y″－2y′＋2y＝e^x，其对应的齐次方程为y″－2y′＋2y＝0，该齐次方程的特征方程为r²－2r＋2＝0，解得r₁_，2＝1±i。故原方程对应的齐次方程的通解为y(＿)＝e^x（c₁cosx＋c₂sinx）。设y^*＝Ae^x为原方程的特解，将其代入原方程可解得A＝1。故原方程的通解为y＝e^x（c₁cosx＋c₂sinx）＋e^x。

单选题微分方程y″－4y′＋5y＝0的通解为（ ）。A ex（C1cos2x＋C2sin2x）B C1e－x＋C2e5xC e2x（C1cosx＋C2sinx）D C1ex＋Ce－5x

题目

相似考题

更多“单选题微分方程y″－4y′＋5y＝0的通解为（ ）。A ex（C1cos2x＋C2sin2x）B C1e－x＋C2e5xC e2x（C1cosx＋C2sinx）D C1ex＋Ce－5x”相关问题

相关内容

单选题微分方程y″－4y′＋5y＝0的通解为（　　）。A ex（C1cos2x＋C2sin2x）B C1e－x＋C2e5xC e2x（C1cosx＋C2sinx）D C1ex＋Ce－5x

更多“单选题微分方程y″－4y′＋5y＝0的通解为（　　）。A ex（C1cos2x＋C2sin2x）B C1e－x＋C2e5xC e2x（C1cosx＋C2sinx）D C1ex＋Ce－5x”相关问题