单选题假设检验时所犯的两类错误的关系是（）。A n一定时，α减小则β减小B n一定时，α减小则β增大C α值改变与β值无关D n一定时，α减小则β不变

题目
单选题
假设检验时所犯的两类错误的关系是（）。
A

n一定时，α减小则β减小

B

n一定时，α减小则β增大

C

α值改变与β值无关

D

n一定时，α减小则β不变

相似考题

1.假设检验时所犯的两类错误的关系是A．n一定时，α减小则β减小B．n一定时，α减小则β增大C．α值改变与β无关D．检验中犯第一类错误则不会犯第二类错误E．等于1-β

2.假设检验的I型错误是指推断结论A.拒绝了实际上成立的HoB.犯了假阴性错误C.犯了概率为β的错误D.接受了实际上不成立的HoE.接受H0时所犯的错误

3.假设检验中,II型错误的定义为“接受无效假设时所犯的错误”。()此题为判断题(对，错)。

4.下列关于I型错误说法正确的是()A、接受Ho时所犯的错误B、拒绝Ho时所犯的错误C、拒绝H1是所犯的错误D、以上说法均不对

更多“假设检验时所犯的两类错误的关系是（）。”相关问题

  • 第1题：

    假设检验的两类错误，以下说法正确的是（ ）。


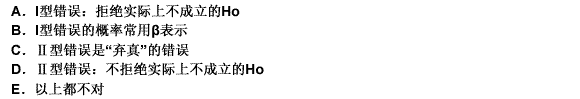    正确答案：D

  • 第2题：

    简述假设检验中两类错误的区别和联系。


    答案：
    解析：
    推断统计；假设检验。 α型错误和卢型错误，前者又称为弃真错误（拒真错误），指当零假设为真时却错误地拒绝了它，因此其大小等于事先设置的显著性水平a，一般为0. 05或0.01；后者又称为取伪错误（纳伪错误），指当零假设为假时却错误地接受了它，其大小为β。 区别：二者性质不同，前提条件不同，这是它们的区别。 联系：它们都是在做假设检验的统计决策时可能犯的错误，决策者同时面临犯两种错误的风 险，因此都极力想避免或者减少它们。但是，在总体间真实差异和样本容量不变的情况下，它们之间是一种此消彼长的关系。要同时减小两种错误的发生可能，可用的办法是增大样本容量。

  • 第3题：

    简述假设检验中的两类错误I型错误与Ⅱ型错误的关系和控制方法。


    答案：
    解析：
    (1)两类错误的关系①a+p不一定等于1。α与卢是在两个前提下的概率。α是拒绝Ho时犯错误的概率，其前提是“Ho为真”；卢是接受Ho时犯错误的概率，其前提是“Ho为假”。②在其他条件不变的情况下，α与β不可能同时减小或增大。许多情况需要在规定α的同时尽量减少β。(1)两类错误的控制①控制d错误的方法就是选用较高的显著性水平。②在规定α的同时尽量减少卢的方法包括：第一种方法是利用已知的实际总体参数与假设参数值之间的大小关系，合理安排拒绝区域的位置，即合理选择左侧检验、右侧检验和双侧检验。第二种方法是增大样本容量。因为样本容量越大，抽样误差σ／越小，抽样分布的形态越高狭陡峭，两侧的面积越小，越能使第二类错误减少。 要回答本题，关键要理解两类错误的含义。第一类，虚无假设H0本来是正确的，但拒绝了H0，这类错误称为弃真错误，即I类错误，这类错误的概率以α表示，因此也叫α型错误。第二类，虚无假设H0本来不正确，却接受了H0，这类错误为取伪错误，即Ⅱ类错误，这类错误的概率以β表示，因此也叫β型错误。

  • 第4题：

    简述假设检验中的两类错误。


    正确答案: 弃真：原假设反映了客观世界的真实情况，却在检验中被作为错误的看法而加以拒绝。
    纳伪：即原假设非真却被当作真实的加以接受。

  • 第5题：

    在假设检验中，α型错误也称为（）

    • A、小概率事件
    • B、接受原假设所犯的错误
    • C、拒绝备择假设所犯的错误
    • D、拒绝虚无假设所犯的错误

    正确答案:D

  • 第6题：

    在假设检验时，可能犯的两类错误是什么？


    正确答案: 即弃真错误、采伪错误，两者变化互相矛盾

  • 第7题：

    假设检验中，II型错误的定义为“接受无效假设时所犯的错误”。


    正确答案:错误

  • 第8题：

    什么是假设检验中的两类错误？


    正确答案:假设检验的结果可能是错误的，所犯的错误有两种类型，一类错误是原假设H0为真却被我们拒绝了，犯这种错误的概率用α表示，所以也称α错误或弃真错误；另一类错误是原假设为伪我们却没有拒绝，犯这种错误的概论用β表示，所以也称β错误或取伪错误。

  • 第9题：

    问答题
    假设检验中的两类错误是什么？如何才能少犯两类错误？

    正确答案： （1）在假设检验中如果H0是真实的，检验后却否定了它，就犯了第一类错误，即α错误或弃真错误；如果H0不是真实的，检验后却接受了它，就犯了第二类错误，即β错误或纳伪错误。
    （2）假设检验中的两类错误是弃真错误和取伪错误。为了减少犯两类错误的概率要做到：
    ①显著水平α的取值不可以太高也不可太低，一般去0.05作为小概率比较合适，这样可以使犯两类错误的概率都比较小；
    ②尽量增加样本容量，并选择合理的实验设计和正确的实验技术，以减小标准误，减少两类错误。
    解析： 暂无解析

  • 第10题：

    问答题
    什么是假设检验中的两类错误？

    正确答案：
    假设检验中所犯的错误有两种类型,一类错误是原假设H0为真却被拒绝了,犯这种错误的概率用α表示,所以也称α错误或弃真错误;另一类错误是原假设为伪却被接受,犯这种错误的概率用β表示,所以也称β错误或取伪错误。
    解析： 暂无解析

  • 第11题：

    问答题
    什么是假设检验，假设检验的两类错误是什么?

    正确答案： 假设检验是指应用有限的样本数据对总体未知的重要信息(如均值、方差和标准差)进行合理的判断。假设检验的第一类错误是指原假设本来是正确的，但是，利用样本数据却做出了拒绝零假设的结论。这类错误发生的概率通常用表示。第二类错误是指原假设本来是错误的，但是，利用样本数据却做出了接收零假设的结论。这类错误发生的概率通常用表示。
    解析： 暂无解析

  • 第12题：

    单选题
    在假设检验中，α型错误也称为（）
    A

    小概率事件

    B

    接受原假设所犯的错误

    C

    拒绝备择假设所犯的错误

    D

    拒绝虚无假设所犯的错误


    正确答案： B
    解析： 暂无解析

  • 第13题：

    假设检验的第二类错误是指

    A.拒绝了实际上成立的H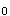
    B.不拒绝实际上成立的H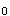
    C.拒绝了实际上不成立的H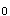
    D.接受实际上错误的H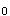
    E.拒绝H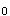时所犯的错误

    答案：D
    解析：
    请掌握两类错误的概念。

  • 第14题：

    简述统计假设检验中两类错误的定义及其关系。


    答案：
    解析：
    (1)假设检验中两类错误：统计检验中两类错误即α错误和β错误。。错误是指当零假设(Ho)成立时，拒绝零假设犯的“弃真”错误，也叫I型错误；p错误是指当零假设不成立时，未拒绝零假设所犯的“取伪”错误，也叫Ⅱ型错误。 (2)两类错误的关系：①α和β是在分别假定零假设为真和零假设为假的情况下讨论的，因此α+β不一定等于1。②在其他条件不变的情况下，α和β不可能同时减少或增大。要想在规定α的同时尽量减小β最直接的方法就是增大样本容量。③I- 在统计学上被称作统计检验力。

  • 第15题：

    假设检验时所犯的两类错误的关系是（）。

    An一定时，α减小则β减小

    Bn一定时，α减小则β增大

    Cα值改变与β值无关

    Dn一定时，α减小则β不变


    B
    略

  • 第16题：

    因为两类错误的存在，所以不能凭假设检验的结果下结论。


    正确答案:错误

  • 第17题：

    在假设检验中，当原假设正确时拒绝原假设，所犯的的错误称为（）。

    • A、第一类错误
    • B、第二类错误
    • C、取伪错误
    • D、取真错误

    正确答案:A

  • 第18题：

    假设检验中的两类错误是什么？如何才能少犯两类错误？


    正确答案: （1）在假设检验中如果H0是真实的，检验后却否定了它，就犯了第一类错误，即α错误或弃真错误；如果H0不是真实的，检验后却接受了它，就犯了第二类错误，即β错误或纳伪错误。
    （2）假设检验中的两类错误是弃真错误和取伪错误。为了减少犯两类错误的概率要做到：
    ①显著水平α的取值不可以太高也不可太低，一般去0.05作为小概率比较合适，这样可以使犯两类错误的概率都比较小；
    ②尽量增加样本容量，并选择合理的实验设计和正确的实验技术，以减小标准误，减少两类错误。

  • 第19题：

    因为有两类错误的存在，所以不能凭假设检验的结果下结论。


    正确答案:错误

  • 第20题：

    什么是假设检验的第一类错误和第二类错误？如何控制两类错误？


    正确答案: 第一类错误是“以真为假”的错误，即原假设是正确但却被拒绝的错误，也称“弃真错误”；第二类错误是“以假为真”的错误，即原假设不正确却被接受的错误，也称“纳伪”错误。这两类错误是一对矛盾体，当我们设法降低第一类错误的概率时，犯第二类错误的概率就会提高；要同时达到减少犯两类错误的可能性，只有通过扩大样本容量来实现。

  • 第21题：

    问答题
    在假设检验时，可能犯的两类错误是什么？

    正确答案： 即弃真错误、采伪错误，两者变化互相矛盾
    解析： 暂无解析

  • 第22题：

    问答题
    简述假设检验中两类错误的区别和联系。

    正确答案： 假设检验中的两类错误指α型错误和β型错误，前者又称为弃真错误，指当零假设为真时错误地拒绝了它，因此其大小等于事先设置的显著型水平，即0.05或0.01；后者又称为取伪错误，指当零假设为假时错误地接受了它。二者性质不同，前提条件不同，这是它们的区别。两类错误的联系是：它们都是在做假设检验的统计决策时可能犯的错误，决策者同时面临犯两种错误的风险，因此都极力想避免或者减少它们，但由于在总体间真实差异不变情况下，它们之间是一种此消彼长的关系，因此，不可能同时减小两种错误的发生可能，常用的办法是固定α的情况下尽可能减小β，比如通过增大样本容量来实现。
    解析： 暂无解析

  • 第23题：

    单选题
    假设检验中两类错误的关系是（　　）。
    A

    α＝β

    B

    α＋β＝1

    C

    α＋β＝1/2

    D

    α＋β不一定等于1


    正确答案： B
    解析：
    假设检验中两类错误的关系是：①α＋β不一定等于1；②在样本容量确定的情况下，α与β不能同时增加或减少。

相关内容