单选题设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。A xB yC zD yf（x2－y2）

题目

单选题

设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。

yf（x²－y²）

相似考题

2.以下选项错误的是A．main（）{ int x,y,z;x=0;y=x-1;z=x+y;}B．main（）{ int x,y,z;x=0,y=x+1;z=x+y;}C．main（）{ int x;intint y;x=0,y=x+1;z=x+y;}D．main（）{ int x,y,z;x=0;y=x+1;z=x+y,}

3.main() { int x,y,z; scanf (“%d%d%d”,&x,&y,&z); printf(“x+y+z=%d\n”,x+y+z); } 输入数据的形式是25，13，10，则程序的输出结果是( )A. x+y+z=48B. x+y+z=35C. x+z=35D. 不确定值

4.(本题满分7分)设函数z=z(x，y)由方程x2+y2+z2=xyz确定，求δz/δy。

更多“设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。”相关问题

第1题：

下面程序执行的结果是( )。 CLEAR X=5 Y=6 Z=7 IF X＞Y IF Z＞8 X=X+Y ELSE X=X+Z ENDIF ENDIF ?X
A．5
B．11
C．12
D．13

正确答案：A
解析：在IF-ENDIF语句中，当表达式为真时，则执行IF语句之后、ELSE或ENDIF语句(以先出现的语句为准)之前的所有命令；当表达式为假时，则执行ELSE语句之后、ENDIF语句之前的所有命令。而且ELSE应该与距离它最近的不带ELSE的IF配对。本题第一个IF没有相应的ELSE配对，且表达式为假，直接输出X的值。
第2题：

设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．

答案：
解析：
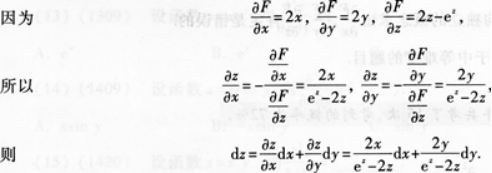
第3题：

若函数z=z(x，y)由方程确定，则=_________.

答案：1、-dx.
解析：
第4题：

判断下列逻辑运算说法是否正确。（1）若X+Y=X+Z，则Y=Z；（）（2）若XY=XZ，则Y=Z；（）（3）若X⊕Y=X⊕Z，则Y=Z；（）

正确答案:错；错；对
第5题：

单选题
设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（　　）。
A
2
B
1
C
e
D
0

正确答案： A
解析：
构造函数F（x，y，z）＝z－e^2x^－^3z－2y。则∂z/∂x＝－F_x′/F_z′＝2e^2x^－^3z/（1＋3e^2x^－^3z），∂z/∂y＝－F_y′/F_z′＝2/（1＋3e^2x^－^3z），故3∂z/∂x＋（∂z/∂y）＝2。
第6题：

填空题
设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。

正确答案： 2
解析：
方程两边同时对x求偏导，则∂z/∂x＝e^2x^－^3z（2－3∂z/∂x），可得∂z/∂x＝2e^2x^－^3z/（1＋3e^2x^－^3z）。同理∂z/∂y＝e^2x^－^3z（－3∂z/∂y）＋2，可得∂z/∂y＝2/（1＋3e^2x^－^3z），所以3∂z/∂x＋∂z/∂y＝6e^2x^－^3z/（1＋3e^2x^－^3z）＋2/（1＋3e^2x^－^3z）＝2（1＋3e^2x^－^3z）/（1＋3e^2x^－^3z）＝2。
第7题：

单选题
设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝（　　）。
A
1
B
2
C
3
D
4

正确答案： A
解析：
根据偏导数的求解方法可知∂z/∂x＝－F_x′/F_z′＝－F₁′/（―aF₁′―bF₂′），∂z/∂y＝－F_y′/F_z′＝－F₂′/（―aF₁′―bF₂′），故a∂z/∂x＋（b∂z/∂y）＝－（aF₁′＋bF₂′）/（―aF₁′―bF₂′）＝1。
第8题：

单选题
设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（　　）。
A
x∂z/∂x＋y∂z/∂y＝0
B
x∂z/∂x－y∂z/∂y＝0
C
y∂z/∂x＋x∂z/∂y＝0
D
y∂z/∂x－x∂z/∂y＝0

正确答案： D
解析：
令u＝x²－y²，则z＝φ（u），∂z/∂x＝φ′（u）·2x＝2xφ′（u），∂z/∂y＝－2yφ′（u），故y∂z/∂x＋x∂z/∂y＝0。
第9题：

单选题
设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（　　）。
A
0
B
1
C
2
D
4

正确答案： B
解析：
构造函数F（x，y，z）＝z－e^2x^－^3z－2y。则∂z/∂x＝－F_x′/F_z′＝2e^2x^－^3z/（1＋3e^2x^－^3z），∂z/∂y＝－F_y′/F_z′＝2/（1＋3e^2x^－^3z），故3∂z/∂x＋（∂z/∂y）＝2。
第10题：

单选题
设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝（　　）。
A
－yf₁′/x－xf₂′/y
B
－yf₁′/x＋xf₂′/y
C
2（－yf₁′/x＋xf₂′/y）
D
2（－yf₁′/x－xf₂′/y）

正确答案： A
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f₁′·（－y/x²）＋f₂′·（1/y），∂z/∂y＝f₁′·（1/x）＋f₂′·（－x/y²），x∂z/∂x－y∂z/∂y＝2（－yf₁′/x＋xf₂′/y）。
第11题：

填空题
设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝____。

正确答案： 1
解析：
根据偏导数的求解方法可知∂z/∂x＝－F_x′/F_z′＝－F₁′/（―aF₁′―bF₂′），∂z/∂y＝－F_y′/F_z′＝－F₂′/（―aF₁′―bF₂′），故a∂z/∂x＋（b∂z/∂y）＝－（aF₁′＋bF₂′）/（―aF₁′―bF₂′）＝1。
第12题：

填空题
设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。

正确答案： 1
解析：
构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－F_x′/F_z′＝－（1＋yz）/（1＋xy），（∂z/∂x）|_（₀_，₁_，－₁_）＝0，又由f（x，y，z）＝e^xyz²，得f_x′＝e^xyz²＋e^xy·2z·z_x′，代入（0，1，－1），得f_x′（0，1，－1）＝e⁰×1×（－1）²＋e⁰×1×2×（－1）×0＝1。
第13题：

A. x-y=0 B. y-z=0 C. x+y=0 D. x+z=0

答案：C
解析：
提示：曲线的参数方程为x=x，y=x，z=0，求出在原点处切线的方向向量，作为法平面的法线向量，写出法平面方程。
第14题：

设函数z=z(x，y)由方程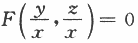确定，其中F为可微函数，且F'2≠0，则=

A.Ax
B.z
C.-x
D.-z

答案：B
解析：
第15题：

设Z=Z(x，Y)是由方程x+y3+z+e2=1确定的函数，求dz

答案：
解析：
利用隐函数求偏导数公式，记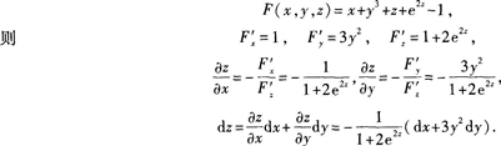
第16题：

单选题
设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝（　　）。
A
e
B
2e
C
0
D
1

正确答案： B
解析：
构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－F_x′/F_z′＝－（1＋yz）/（1＋xy），（∂z/∂x）|_（₀_，₁_，－₁_）＝0，又由f（x，y，z）＝e^xyz²，得f_x′＝e^xyz²＋e^xy·2z·z_x′，
代入（0，1，－1），得f_x′（0，1，－1）＝e⁰×1×（－1）²＋e⁰×1×2×（－1）×0＝1。
第17题：

单选题
设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝（　　）。
A
－yf₁′/x＋xf₂′/y
B
2（－yf₁′/x＋xf₂′/y）
C
－yf₁′/x＋2xf₂′/y
D
－yf₁′/x＋f₂′/y

正确答案： A
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f₁′·（－y/x²）＋f₂′·（1/y），∂z/∂y＝f₁′·（1/x）＋f₂′·（－x/y²），x∂z/∂x－y∂z/∂y＝2（－yf₁′/x＋xf₂′/y）。
第18题：

单选题
设方程x2＋y2＋z2＝4z确定可微函数z＝z（x，y），则全微分dz等于（　　）。[2014年真题]
A
（ydx＋xdy）/（2－z）
B
（xdx＋ydy）/（2－z）
C
（dx＋dy）/（2＋z）
D
（dx－dy）/（2－z）

正确答案： C
解析：
对等式两边分别同时求导，得：2xdx＋2ydy＋2zdz＝4dz。所以dz＝（xdx＋ydy）/（2－z）
第19题：

填空题
设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝____。

正确答案： yf₁′+f₂′/y-yg′/x²
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f₁′y＋f₂′·（1/y）＋g′·（－y/x²）＝f₁′y＋f₂′/y－yg′/x²。
第20题：

单选题
设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。
A
x
B
y
C
z
D
yf（x²－y²）

正确答案： C
解析：
由x＋z＝yf（x²－z²），可得∂z/∂x＝－（1－y·2xf′）/（1＋2yzf′），∂z/∂y＝－（－f）/（1＋2yzf′），故有（z∂z/∂x）＋（y∂z/∂y）＝（x－yf＋2xyzf′＋yf）/（1＋2yzf′）＝x。
第21题：

填空题
设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝____。

正确答案： 2(-yf₁′/x+xf₂′/y)
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f₁′·（－y/x²）＋f₂′·（1/y），∂z/∂y＝f₁′·（1/x）＋f₂′·（－x/y²），x∂z/∂x－y∂z/∂y＝2（－yf₁′/x＋xf₂′/y）。
第22题：

单选题
利用变量替换u＝x，v＝y/x一定可以把方程x∂z/∂x＋y∂z/∂y＝z化为新方程（　　）。
A
u∂z/∂u＝z
B
∂z/∂v＝z
C
u∂z/∂v＝z
D
v∂z/∂u＝z

正确答案： B
解析：
由x∂z/∂x＋y∂z/∂y＝z，得∂z/∂x＝（∂z/∂u）·1＋（∂z/∂v）（－y/x²），∂z/∂y＝（1/x）（∂z/∂v）。
故x∂z/∂x＋y∂z/∂y＝x∂z/∂u－（y/x）（∂z/∂v）＋（y/x）（∂z/∂v）＝x∂z/∂u＝z。
而u＝x，故u∂z/∂u＝z。
第23题：

单选题
设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝（　　）。
A
2（yf₁′/x＋xf₂′/y）
B
2（yf₁′/x－xf₂′/y）
C
2（－yf₁′/x＋xf₂′/y）
D
2（－yf₁′/x－xf₂′/y）

正确答案： C
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f₁′·（－y/x²）＋f₂′·（1/y），∂z/∂y＝f₁′·（1/x）＋f₂′·（－x/y²），x∂z/∂x－y∂z/∂y＝2（－yf₁′/x＋xf₂′/y）。
第24题：

单选题
由方程f（y/x，z/x）＝0确定z＝z（x，y）（f可微），则x∂z/∂x＋y∂z/∂y＝（　　）。
A
－z
B
z
C
－y
D
y

正确答案： C
解析：
由f（y/x，z/x）＝0可得，∂z/∂x＝－[f₁′·（－y/x²）＋f₂′·（－z/x²）]/（f₂′/x），∂z/∂y＝－（f₁′/x）/（f₂′/x），则x∂z/∂x＋y∂z/∂y＝－（―yf₁′/x―zf₂′/x＋yf₁′/x）/（f₂′/x）＝z。

单选题设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（ ）。A xB yC zD yf（x2－y2）

题目

相似考题

更多“设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（ ）。”相关问题

相关内容

单选题设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。A xB yC zD yf（x2－y2）

更多“设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。”相关问题