对任意的实数k，直线y-2=k（x+1）恒过定点M，则M的坐标是（）。A、（1，2）B、（1，-2）C、（-1，2）D、（-1，-2）
题目
对任意的实数k，直线y-2=k（x+1）恒过定点M，则M的坐标是（）。
- A、（1，2）
- B、（1，-2）
- C、（-1，2）
- D、（-1，-2）
相似考题
更多“对任意的实数k，直线y-2=k（x+1）恒过定点M，则M的坐标是（）。A、（1，2）B、（1，-2）C、（-1，2）D、（-1，-2）”相关问题
-
第1题：
设直线的方程为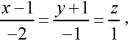
则直线：
(A)过点(1,-1,0)，方向向量为2i + j-k
(B)过点(1,-1,0)，方向向量为2i - j + k
(C)过点(-1,1,0)，方向向量为-2i - j + k
(D)过点(-1,1,0)，方向向量为2i + j - k答案：A解析：设直线L过点M0（x0，y0，z0），它的一个方向向量为s=(m,n,p),则直线L的方程为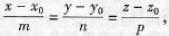
此方程称为直线的对称式方程， 如设参数t如下：
此方程组称为直线的参数式方程。 -
第2题：
如果函数y=kx+b的图像经过A（1,2）和B（0,1），则k=（ ）A.-5
B.1
C.2
D.5答案：B解析： -
第3题：
已知点C（2,-3）,M（1,2）,N（-1,-5）,则点C到直线MN的距离等于（ ）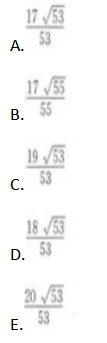
答案：A解析：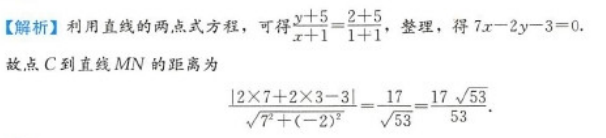
-
第4题：
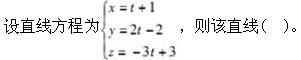A.过点(-1，2，-3)，方向向量为i+2j-3k
B.过点(-1，2，-3)，方向向量为-i-2j+3k
C.过点(1，2，-3)，方向向量为i-2j+3k
D.过点(1，-2，3)，方向向量为-i-2j+3k答案：D解析：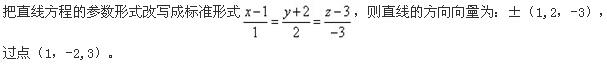
-
第5题：
对任意的实数k，直线y-2=k(χ+1)恒过定点M，则M的坐标是( )。A、(1，2)
B、(1，-2)
C、(-1，2)
D、(-1，-2)答案：C解析：当x+l=0时，无论直线斜率为多少，都有y-2=0，此时x=-1，y=2，则M(-1，2)。故选择C。 -
第6题：
关于二次函数y=2-(x+1)2的图象,下列说法正确的是( )。A.图象开口向上
B.图象的对称轴为直线x=1
C.图象有最低点
D.图象的顶点坐标(-1，2)答案：D解析：由二次函数图象的性质可知，其开口方向向下，有最大值2，对称轴为x=-1，顶点坐标(-1，2)。二次函数y=a(x+h)2+k(α≠0)中，α决定了二次函数图象的开口方向，顶点坐标为(-h，k)。 -
第7题：
已知曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0，则点P的坐标是（）．
- A、（1，-1，2）
- B、（1，1，2）
- C、（-1，1，2）
- D、（-1，-1，2）
正确答案:B -
第8题：
一定温度下，1，2两反应的标准摩尔吉布斯自由能间的关系为ΔrGθm1=2ΔrGθm2则两反应标准平衡常数间的关系为Kθ2 =（Kθ1）2。
正确答案:错误 -
第9题：
设随机变量X的概率分布为P{X=k}=θ（1-θ）k-1，k=1，2，L，其中0<θ<1，若P{X≤2}=5/9，则P{X=3}=（）。
正确答案:4/27 -
第10题：
问答题已知m个向量α(→)1，α(→)2，…，α(→)m线性相关，但其中任意m－1个都线性无关，证明： （1）如果存在等式k1α(→)1＋…＋kmα(→)m＝0(→)，则这些系数k1，…，km或者全为零，或者全不为零。 （2）如果存在两个等式k1α(→)1＋…＋kmα(→)m＝0(→)，l1α(→)1＋…＋lmα(→)m＝0(→)，其中l1≠0，则k1/l1＝k2/l2＝…＝km/lm。正确答案：
(1)假设k1,k2,…,km中有一个为零,k1=0,则k2α2+…+kmαm=0,根据α2,α3,…,αm线性无关得到k2=…=km=0,因此k1,k2,…,km全为零或者全不为零。
(2)由(1)可知,l1≠0,则l2≠0,…,lm≠0,有k1l1α1+…+kml1αm=0,k1l1α1+…+k1lmαm=0,两式相减得到(k2l1-k1l2)α2+…+(kml1-k1lm)αm=0,根据α2,α3,…,αm线性无关得到kil1-k1li=0(i=2,3,…,m),即k1/l1=ki/li(i=2,…,m)。解析： 暂无解析 -
第11题：
单选题过点（－1，2，3）垂直于直线x/4＝y/5＝z/6且平行于平面7x＋8y＋9z＋10＝0的直线是（ ）。A（x＋1）/1＝（y－2）/（－2）＝（z－3）/1
B（x＋1）/1＝（y－2）/2＝（z－3）/2
C（x＋1）/（－1）＝（y－2）/（－2）＝（z－3）/1
D（x－1）/1＝（y－2）/（－2）＝（z－3）/1
正确答案： B解析：
直线x/4＝y/5＝z/6的方向向量为s＝4，5，6，平面7x＋8y＋9z＋10＝0的法向量为n＝7，8，9。显然ABC三项中的直线均过点（－1，2，3）。A项中直线的方向向量为s1＝（1，－2，1），有s1⊥s，s1⊥n，可见A中直线与已知直线x/4＝y/5＝z/6垂直，与平面7x＋8y＋9z＋10＝0平行。 -
第12题：
单选题对任意的实数k，直线y-2=k（x+1）恒过定点M，则M的坐标是（）。A（1，2）
B（1，-2）
C（-1，2）
D（-1，-2）
正确答案： B解析： 当x+1=0时，无论直线斜率为多少，都有y-2=0，此时x=-1，y=2，则M（-1，2）。故选择C。 -
第13题：
过(1，2)点且平行于向量a=(2，2)的直线方程为＿＿＿＿＿．答案：解析：【答案】x-y+1=0 【考情点拨】本题主要考查的知识点为直线的斜截式方式．
【应试指导】设所求直线为L，∵ka=1，L∥a，∴kL=ka=1，又∵L过点(1，2)，∴L的方程为y-2=1×(x-1)，即x-y+1=0． -
第14题：
若集合M={（x，y）｜ 3x一2y=-1），N={（x，y）｜ 2x+3y=8}，则M∩N=（）A.（1，2）
B.{1，2}
C.{（1，2）}
D.φ答案：C解析： -
第15题：
不等式∣x+3∣-∣x-1∣≤a2-3a对任意实数x恒成立,则实数a的取值范围为A.（-∞,-1]U[4,+∞）
B.（一∞,一2]U[5,+∞）
C.[1,2]
D.（一∞,1]U[2,+∞）
E.以上选项均不正确答案：A解析：∣x+3∣-∣x-1∣≤4，a2-3a≥4,解得a≤-1或a≥4 -
第16题：
对任意的实数k，直线y-2=k(x+1)恒过定点M，则M的坐标是( )。A、(1，2)
B、(1，一2)
C、(一1、2)
D、(-1，-2)答案：C解析：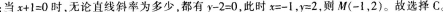
-
第17题：
设球面方程为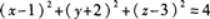
，则该球的球心坐标与半径分别为()．A.(-1，2，-3)；2
B.(-1，2，-3)；4
C.(1，-2，3)；2
D.(1，-2，3)；4答案：C解析：对照球面方程的基本形式可知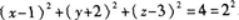
因此球心坐标为(1，-2，3)，半径为2，故选C． -
第18题：
特征方程的根s=σ，为实数根有m重极点则对应的时域表达式为(k1+k2t+……+kmtm-1)eσt。（）
正确答案:正确 -
第19题：
迭代过程xk+1=φ（xk）（k=1，2，...）收敛的充要条件是（）。
正确答案:|φ′（x）|<1 -
第20题：
已知f（k）={1，2，-2，1}，h（k）={3，4，2，4}，求f（k）*h（k）=（）
正确答案:{3,10,4,3,8,-6,4 -
第21题：
对反应式（1）A+B=2C和（2）（1/2）A+（1/2）B=C，在相同条件下存在关系（）
- A、ΔrGΘm（1）=2ΔrGΘm（2）；KΘ（1）=KΘ（2）
- B、ΔrGΘm（1）=22ΔrGΘm（2）；{KΘ（1）=KΘ（2）}2
- C、ΔrGΘm（1）=2ΔrGΘm（2）；{KΘ（1）=KΘ（2）}2
- D、ΔrGΘm（1=）2ΔrGΘm（2）；KΘ（1）=KΘ（2）
正确答案:B -
第22题：
单选题对任意输入的实数X，下列程序执行后K的可能输出值为（ ）。 READ(*，*)X K=2*COS(X) PRINT*，K ENDA在区间[-2，2]中的一个实数值
B0,1，-1
C在区间(-2，2)中的一个实数值
D0,l，-1,2，-2
正确答案： A解析： 由于COS(X)的结果在区间[-1,1]中,而K为整型变量,故2*COS(X)只能为0,1,-1,2,-2. -
第23题：
填空题设随机变量X的分布律为P{X＝k}＝1/2k（k＝1，2，…），则P{X＞2}＝____。正确答案： 1/4解析：
P{X＞2}＝1－P{X≤2}＝1－P{X＝1}－P{X＝2}＝1－1/2－1/22＝1/4。