简述四节点四边形等参数单元的平面问题分析过程。
题目
简述四节点四边形等参数单元的平面问题分析过程。
相似考题
更多“简述四节点四边形等参数单元的平面问题分析过程。”相关问题
-
第1题:
静定平面桁架的内力计算方法有( )。A.截面法
B.节点法
C.平行四边形法则
D.二力平衡公理
E.平面汇交力系计算内力答案:A,B解析:静定平面桁架的内力计算方法有截面法、节点法 -
第2题:
在学习了平行四边形、三角形的中位线定理后,某老师设计了一个教学目标。
① 进一步理解三角形中位线定理和平行四边形判定定理
② 运用三角形中位线定理、平行四边形判定定理解决问题
③ 提高发现解决能力
他的教学过程设计包含以下一道例题:如图1,在四边形ABCD中,EFGH分别是AB、BC、CD、DA中点,
问题一、求证四边形EFGH是平行四边形。
问题二、如何改变问题条件,从而分别得到菱形、矩形、正方形。
针对上述材料,完成以下任务
(1)结合目标分析该例题设计意图(10分)
(2)类比上述例题问题二设计一个新问题,使之符合教学目标③要求(8分)
(3)设计该例题简要教学流程(8分)并给出解题的小结提纲(4分) 答案:解析:本题主要考查教学设计相关内容。
答案:解析:本题主要考查教学设计相关内容。 -
第3题:
采用杆系有限元法分析挡土结构的过程描述错误的是()。
- A、结构理想化
- B、各节点满足变形协调条件
- C、建立单元所受荷载与单元节点位移之间的关系
- D、结构集中化
正确答案:D -
第4题:
“正方形是平面内每个内角都是直角的四边形。”作为概念是否正确?
正确答案:错误 -
第5题:
平面三角形单元和平面刚架单元具有相同的()
- A、单元形状
- B、节点数
- C、位移分量数
- D、转换矩阵
正确答案:C -
第6题:
进行直梁有限元分析,平面刚架单元上每个节点的节点位移为()和()
正确答案:挠度;转角 -
第7题:
例如,“菱形→等边四边形→平行四边形→四边形”这是一个()过程。
- A、弱抽象
- B、浅层抽象
- C、深层抽象
- D、强抽象
正确答案:D -
第8题:
简述四边形钢管铁塔的优缺点。
正确答案:优点是占地面积小,安装时不需要大型机械,对运输条件要求比较低。相对于四边形角钢塔,抗风能力较强。
缺点是加工要求较高,塔柱钢管之间的连接需要使用法兰等精加工部件。加上钢管单价比角钢高,故总的建设成本较高。
四边形钢管塔比较适合于施工场地小、运输较为困难的地点。 -
第9题:
简述平面钢架问题有限元法的基本过程。
正确答案: 1)力学模型的确定,
2)结构的离散化,
3)计算载荷的等效节点力,
4)计算各单元的刚度矩阵,
5)组集整体刚度矩阵,
6)施加边界约束条件,
7)求解降价的有限元基本方程,
8)求解单元应力,
9)计算结果的输出。 -
第10题:
问答题简述四节点四边形等参数单元的平面问题分析过程。正确答案: (1)通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;
(2)通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;
(3)将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵
(4)用虚功原理球的单元刚度矩阵,最后用高斯积分法计算完成。解析: 暂无解析 -
第11题:
填空题进行直梁有限元分析,平面刚架单元上每个节点的节点位移为()和()正确答案: 挠度,转角解析: 暂无解析 -
第12题:
问答题教学设计题:试分析平行四边形面积公式推导过程中体现的数学思想。正确答案: 平行四边形面积公式推导采用的割补拼接法,通过将平行四边形进行分割拼接成长方形然后计算其面积的方法体现了数学中的转化思想。转化思想是由一种形式变换成另一种形式的思想方法,而其本身的大小是不变的。解析: 暂无解析 -
第13题:
在学习了平行四边形、三角形的中位线定理后,某教师设计了一节习题课的教学目标:
①进一步理解三角形中位线定理、平行四边形的判定定理;
②能综合运用三角形中位线定理、平行四边形的判定定理等知识解决问题;
③提高发现和提出数学问题的能力。
他的教学过程设计中包含了下面的一道例题:
如图1,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
问题一求证:四边形EFGH是平行四边形;
问题二如何改变问题中的条件.才能分别得到一个菱形、矩形、正方形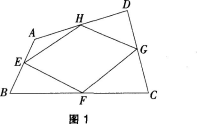
针对上述材料,完成下列任务:
(1)结合该教师的教学目标,分析该例题的设计意图;
(2)类比上述例题中的问题二,设计一个新问题,使之符合教学目标③的要求;
(3)设计该例题的简要教学流程,并给出解题后的小结提纲。答案:解析:(1)设计意图: a.解决这道题目的问题一首先需要学生利用三角形的中位线定理得到四边形EFGH的对边平行且相等(或两组对边分别平行)的结论,其次利用平行四边形的判定定理,判定四边形是乎行四边形。因此在练习过程中可以加深学生对三角形中位线定理和平行四边形判定定理的理解。又因为需要同时利用两个定理进行求解,所以可以提高学生对两者的综合应用能力,顺利达成教学目标①和②。
b.问题一可以一题多解,可以锻炼学生的发散思维,还能够加深学生对平行四边形判定定理的应用。此外问题二是一道开放性的题目.由学生自己设定条件自主解答,因此可以达成教学目标③。
c.问题二的解决又需要学生从对角线的角度出发,对平行四边形及特殊的平行四边形的性质和判定有深刻的认识,通过本问题的练习,兼顾到了教学目标①和②。
(2)问题:连接HF,EG交于一点O,取0E,OG,OH,OF的中点分别为P,M,N,Q,连接PN,PQ,MN,MQ,证明四边形PQMN是平行四边形。改变题干中什么条件四边形PQMN会是矩形、菱形、正方形,并说明理由。
(3)教师呈现图片和问题,学生独立进行思考、作答。如果学生作答顺利,将课堂放手交还给学生,如果学生遇到了一定的难度,可以组织学生小组讨论,共同探讨或者教师通过问题进行启发引导,降低题目的难度,对于问题一可以提出问题:
追问一:平行四边形的判定定理有哪些
追问二:从题干和图形中,我们可以得到哪些边角相等,哪些边平行
对于问题二可以提出问题:
追问:平行四边形在什么样的情况下可以转变成菱形、矩形、正方形
学生进行充分思考,多数学生得出结果之后,指定学生进行回答。要求说明结果和做题的思路。教师及时给予积极有效的反馈点评,针对学生的回答进行总结。最后通过多媒体或黑板直观的呈现答案。
小结提纲1:解决有关平行四边形类的题目时,往往先利用其他四边形或三角形的相关几何知识得到相关信息,进而求解。因此需要我们从整体上把握几何图形的性质和判定定理,以及其中的内在联系。
小结提纲2:平行四边形的判定通常可以从边、角以及边角之间的位置、数量关系来进行判定,特殊的平行四边形如菱形、矩形、正方形具有平行四边形性质的所有性质,可以分别找出与平行四边形之间的联系与区别。
小结提纲3:证明一个四边形是平行四边形,要找这个四边形对边或对角线存在的关系。证明一个四边形是矩形、菱形、正方形,可以先从这个图形是平行四边形出发,在平行四边形的基础之上,添加适当的边、角、对角线的条件。证明得到矩形、菱形、正方形。 -
第14题:
复用段保护环上各节点参数设置的顺序和方向有何规定?若节点参数设置不连续有何问题?若方向设反有何问题?
正确答案: (1)沿东发(主环)方向,复用段节点号从“0”开始,逐一递增,最大节点号为节点数减一,保护倒换恢复时间为600秒。
(2)节点参数不连续,保护倒换会出现异常,在一些情况下可正常倒换;在一些情况下正常倒换后会出现无法恢复的现象。
(3)若方向设反,保护倒换无法成功 -
第15题:
过程控制通过预先设定(),在服务追踪过程中,在不同节点检查各个参数值,与目标值进行比较,将偏差反馈个服务制定或指导人员,随后进行调整。
- A、过程节点
- B、流程节点
- C、参数值
- D、参数指标
正确答案:B,D -
第16题:
有限元位移法中单元分析的主要内容由节点位移求内部任一点的位移,由节点位移求单元应变,应力和()。
正确答案:节点力 -
第17题:
简述平行四边形公理。
正确答案:作用在物体上某一点的两个力,可以合成作用于该点的一个合力,合力的大小和方向由这两个力为邻边所构成的平行四边形的对角线确定。 -
第18题:
剖切平面任意斜截一正方体所得的图形一般为()。
- A、正方形
- B、长方形
- C、任意四边形
- D、平行四边形
正确答案:D -
第19题:
简述等参数单元的概念。
正确答案:坐标变换中采用节点参数的个数等于位移模式中节点参数的个数,这种单元称为等参单元。 -
第20题:
复用段保护环上各节点节点参数设置不连续有何问题
正确答案: 节点参数不连续,保护倒换会出现异常,在一些情况下可正常倒换;在一些情况下正常倒换后会出现无法恢复的现象。 -
第21题:
单选题平面三角形单元和平面刚架单元具有相同的()A单元形状
B节点数
C位移分量数
D转换矩阵
正确答案: B解析: 暂无解析 -
第22题:
单选题例如,“菱形→等边四边形→平行四边形→四边形”这是一个()过程。A弱抽象
B浅层抽象
C深层抽象
D强抽象
正确答案: A解析: 暂无解析 -
第23题:
问答题简述等参数单元的概念。正确答案: 坐标变换中采用节点参数的个数等于位移模式中节点参数的个数,这种单元称为等参单元。解析: 暂无解析
