若方程X^2+（m-2）X+5-m=0的二根都比2大，实数m的范围是（）A、m≥-4B、m≥-3C、m≤-3D、m≤-4
题目
若方程X^2+（m-2）X+5-m=0的二根都比2大，实数m的范围是（）
- A、m≥-4
- B、m≥-3
- C、m≤-3
- D、m≤-4
相似考题
参考答案和解析
正确答案:D
更多“若方程X^2+（m-2）X+5-m=0的二根都比2大，实数m的范围是（）A、m≥-4B、m≥-3C、m≤-3D、m≤-4”相关问题
-
第1题：
—单缝宽度a=1X10-4 m，透镜焦距f=0. 5m，若用λ= 400nm的单色平行光垂直入射，中央明纹的宽度为：
A. 2X10-3 m B.2X10-4 m C. 4X10-4 m D. 4X10-3 m答案：D解析：提示：中央明纹宽度。 -
第2题：
已知函数f(x)是定义在R上的奇函数，若f(x)的最小正周期为4，且f(1)>0,f(3)=
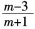
则m的取值范围是( )。A.-3＜m＜1
B.m＞1或m＜-3
C.-1＜m＜3
D.m＞3或m＜-1答案：C解析：
-
第3题：
函数(x)=x2+2(m-1)x+2在区间(-∞，4)上是减函数，则实数m的取值范围是( )A.m≥-3
B.m=-3
C.m≤-3
D.m≥3答案：C解析：【考情点拨】本题主要考查的知识点为减函数的性质． 【应试指导】由已知条件(x)=x2+2(m-1)x+2(x)=(x+m-1)2-(m-1)2+2，故(x)的对称轴为x=1-m，又∵(x)在(-∞，4)上是减函数，∴1-m≥4，即m≤-3． -
第4题：
已知三点A（1,-2）,B（m,2）,且线段AB的垂直平分线的方程是x+2y-2=0,则实数m的值为（ ）A.-2
B.-7
C.3
D.1
E.2答案：C解析：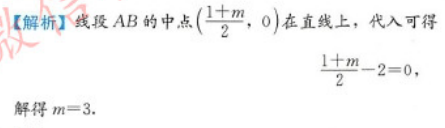
-
第5题：
曲线C1：x2+y2-2x=0与曲线C2：y(y-mx-m)=0有4个不同交点，则实数m取值( )。
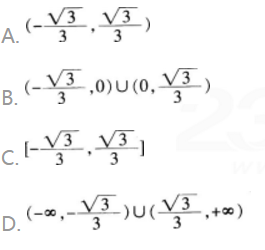答案：B解析：
-
第6题：
已知集合A={x∣x2-3x-4>0}，集合B={x∣m+1≤x≤4m)，若B∈A，则实数m的取值范围为( )。
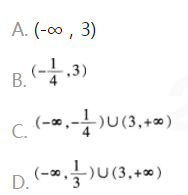答案：D解析：
-
第7题：
若w、x、y、z、m均为int型变量，则执行下列的语句后m的值是（）。 w=2，x=3，y=4，z=5； m=（w＜x）w：x； m=（m＜z）m：z； m=（m＜y）m：y；
- A、2
- B、3
- C、5
- D、4
正确答案:A -
第8题：
M0—M15中，M0数值都为1，其它都为0，那么，K4M0数值等于（）。
- A、4
- B、3
- C、2
- D、1
正确答案:D -
第9题：
FX系列PLC中，M0-M7中M0、M1数值都为1，其它都为0。那么K4M0数值等于（）。
- A、l
- B、2
- C、3
- D、4
正确答案:C -
第10题：
以下程序段的输出结果是（） int a[7]={9，15，7，-3，0，11，15}，m，n，i；for（m=n=0，i=1；i<7；i++） if（a[i]>a[m]）m=i； elseif（a[i]printf（"%d，%d/n"，m，n）
- A、15，-3
- B、6，3
- C、1，3
- D、2，4
正确答案:C -
第11题：
单选题WMO把直接辐射（）定义为有日照。A≥150W•m-2；
B≥120W•m-2；
C≥100W•m-2；
D≥80W•m-2；
正确答案： A解析： 暂无解析 -
第12题：
单选题若w、x、y、z、m均为int型变量，则执行下列的语句后m的值是（）。 w=2，x=3，y=4，z=5； m=（w＜x）w：x； m=（m＜z）m：z； m=（m＜y）m：y；A2
B3
C5
D4
正确答案： D解析： 条件表达式“ab：c”的含义是：当a为真时，其值等于表达式b的值，当a为假时，其值等于表达式c的值。 表达式运算过程：第1个表达式：w-2＜x=3为真，所以返回w的值，即m=w=2；第2个表达式；m-2＜z=5为真，所以返回m的值，即m=2；第3个表达式；w=2＜y=4为真，所以返回m的值，即m=2。 -
第13题：
已知关于x的方程3x一2m=4的解是x=m，则m的值是________．答案：解析：
-
第14题：
已知集合A={x|x2-3x-4>0}，集合B={x|m+1≤x≤4m}，若B?A，则实数m的取值范围为()。A.(-∞，3)
B.(-(1/4)，3)
C.(-∞，-(1/4))∪(3，+∞)
D.(-∞，1/3)∪(3，+∞)答案：D解析：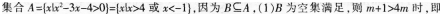
-
第15题：
不等式2x2+3mx+2m>0的解集是实数集，则m的取值范围是( )
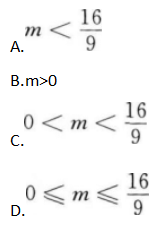答案：C解析：【考情点拨】本题主要考查的知识点为不等式的解集． 【应试指导】由2x2+3mx+2m>0的解集为R，又因为抛物线的开口向上，所以方程2x2+3mx+2m=0无实根，
-
第16题：
一横波的波动方程是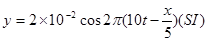
t=0.25s，距离原点（x=0）处最近的波峰位置为（ ）。A、 ±2、5m
B、 ±7、5m
C、 ±4、5m
D、 ±5m答案：A解析：t=0.25s时，波形为
波峰位置即质点振幅最大的位置。波峰位置的条件为：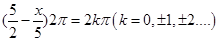
可求得距离原点x=0处最近的波峰位置为±2.5m。 -
第17题：
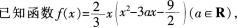
若函数f(x)的图象上点P(1，m)处的切线方程为3x-y+b=0，则m的值为__________。答案：解析：
-
第18题：
假定w、x、y、z、m均为int型变量；有如下程序段： w=1；x=2；y=3；z=4； m=（w
- A、4
- B、3
- C、2
- D、1
正确答案:D -
第19题：
已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。
正确答案: 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
（1）若p为真，则q为假。
p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
取交集得到，m≥3：
（2）若q为真，则p为假。
q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
取交集得到：1综上所述m≥3或1 -
第20题：
M0—M15中M0数值都为1其它都为0那么K4M0数值等于多少（）
- A、4
- B、3
- C、2
- D、1
正确答案:D -
第21题：
n=4时m的最大取值为（）
- A、4
- B、±4
- C、3
- D、0
正确答案:C -
第22题：
WMO把直接辐射（）定义为有日照。
- A、≥150W•m-2；
- B、≥120W•m-2；
- C、≥100W•m-2；
- D、≥80W•m-2；
正确答案:B -
第23题：
问答题已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。正确答案： 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
（1）若p为真，则q为假。
p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
取交集得到，m≥3：
（2）若q为真，则p为假。
q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
取交集得到：1综上所述m≥3或1解析： 暂无解析 -
第24题：
填空题已知方程x2＋(4－2m)x＋m2－5＝0的两根之积是两根之和的2倍，则m＝____．正确答案： 1或3解析：
由韦达定理可知，m2－5＝－2(4－2m)，解得m＝1或3．