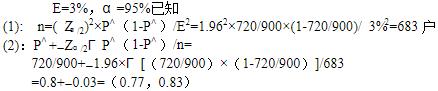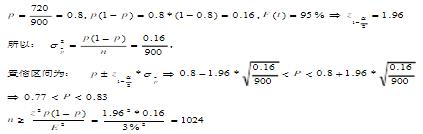某大型企业要提出一项改革措施，为了估计该城市中赞成该项改革的人数的比例，要求边际误差不超过0.03，置信水平为95%，应抽取的样本量为（）A、1065B、1066C、1067D、1068
题目
某大型企业要提出一项改革措施，为了估计该城市中赞成该项改革的人数的比例，要求边际误差不超过0.03，置信水平为95%，应抽取的样本量为（）
- A、1065
- B、1066
- C、1067
- D、1068
相似考题
更多“某大型企业要提出一项改革措施，为了估计该城市中赞成该项改革的人数的比例，要求边际误差不超过0.03，置信水平为95%，应抽取的样本量为（）A、1065B、1066C、1067D、1068”相关问题
-
第1题：
研究者要估计某地区居民2013年的旅游支出。经验表明，总体标准差为5000元，如要求在95%的置信度水平下最大允许误差不超过500元，应该抽取的样本容量等于（ ）。（注：）
正确答案：C
-
第2题：
拥有工商管理学士学位的大学毕业生年薪的标准差大约为2000元，假定想要以95％的置信水平估计年薪的置信区间，允许的估计误差不超过400元，应抽取多大的样本容量答案：解析：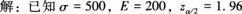
-
第3题：
小区的写字楼月租金的标准差为80元，要估计总体均值95%的置信区间，希望的允许误差为15元，应抽取的样本量为（ ）。A.100
B.110
C.120
D.130答案：B解析：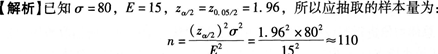
-
第4题：
欲对某区居民的消费支出进行估计。根据以往调查结果，居民消费支出的标准差为300元。若将估计的允许误差控制在50元以内，在95%的置信水平下应抽取的样本量为（）。（备注：Z0.025=1.96）A.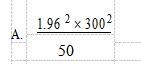
B.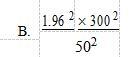
C.
D.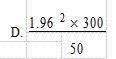
答案：B解析： -
第5题：
企业要提出一项改革措施，为估计职工中赞成该项改革的人数比例，要求允许误差不超过0．03，置信水平为90%，应抽取的样本量为（ ）。A.552
B.652
C.757
D.852答案：C解析：因为总体比例π未知，取π=0．5，而za／2=z0.1/2=1．65，E=0．03，所以应抽取
-
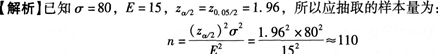
第6题：
90%的置信水平意味着( )。A.预计误差率等于10%
B.估计值和总体实际值之间的差异不超过10%
C.样本结果偏离总体特征的程度不超过特征范围的可能性为90%
D.如果置信水平等于95%，则需要更大的样本量答案：C解析：C置信水平为90%是指样本结果偏离总体真实特征的程度有90%的可能性不超过特定范围。选项A不正确，置信水平为90%不意味着预计误差率就是10%。选项B不正确，置信水平为90%并不意味着估计值和总体实际值之间的差异不超过10%。选项D不正确，如果置信水平为95%，样本量应当减小。 -
第7题：
从某市的居民住户中随机重复抽取900户，其中720户拥有电视机。据此，你认为在95%的置信水平下，该城市居民的电视机普及率大概为多少？在同样的置信水平下，应该抽取多少居民户才能保证电视机普及率的估计误差不超过3%？
据题意，分别列式计算如下：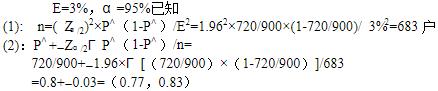
该城市居民的电视机普及率大概为77-83%，应抽取683户居民户才能保证电视机普及率的估计误差不超过3%。
略 -
第8题：
从一个方差为900的总体中，抽取225个个体作为样本。在95%的置信水平下，边际误差是（）。
- A、15
- B、2
- C、3.92
- D、4
正确答案:C -
第9题：
我们想进行一项研究，以确定一个城市中有多少百分之多少的选民将愿意投票给现任市长。在95%的置信水平下，为使边际误差不超过4，估计总体比率所需的最小样本容量是多少？（）
- A、625
- B、626
- C、600
- D、601
正确答案:D -
第10题：
为了估计某城市中拥有汽车的家庭比例，抽取500个家庭的一个样本，得到拥有汽车的家庭比例为35%，这里的35%是（）
- A、参数值
- B、统计量的值
- C、样本量
- D、变量
正确答案:B -
第11题：
企业要提出一项改革措施，为估计职工中赞成该项改革的人数的比例，要求允许误差不超过0.03，置信水平为90%，应抽取的样本量为（）。
- A、552
- B、652
- C、757
- D、852
正确答案:C -
第12题：
问答题某超市想要估计每个顾客平均每次购物花费的金额。根据过去的经验，标准差大约为 120元，现要以95%的置信水平估计每个顾客平均每次购物金额的置信区间，并要求边际误差不超过20元，若采用不重复抽样，要抽取多少个顾客作为样本？正确答案： 已知：
σ=120 Δ= 20 1-α= 0.95 α/2= 0.025
Φ（Z0.025）=0.5–0.025=0.475
查正态分布表得：Z0.025=1.96
N0=（Z0.025σ/Δ）2=（1.96×120/20）2=138.3≈139
因为N→∝，故不重复抽样n=n0/（1+n0/N）=n0=139（名）解析： 暂无解析 -
第13题：
一项研究中要对贫困户的比例进行推断。在95%的置信度下要求误差不超过±3%。采用重置简单随机抽样中，已知z0.025=1.96，则以下说法正确的有( )。A.如果总体中贫困户的比例估计为30%，则必要样本容量为896人
B.如果总体中贫困户的比例估计为30%，则必要样本容量为897人
C.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人
D.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人
E.如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算答案：B,C解析：AB两项，贫困生比例已知时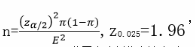
E≤士3%，π= 30%，计算得n≥896.4，n≈897人；CDE三项，贫困生比例信息缺失时，按照最大方差原则应假定贫困户的比例为50%，此时按照公式计算得到样本容量n=1067.1，为控制误差大小，必要样本容量为1068人。 -
第14题：
一项研究中要对贫困户的比例进行推断。在95%的置信度下要求误差不超过±3%。采用重置简单随机抽样中，已知
，则以下说法正确的有（）。A．如果总体中贫困户的比例估计为30%，则必要样本容量为896人
B．如果总体中贫困户的比例估计为30%，则必要样本容量为897人
C．如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人
D．如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人
E．如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算答案：B,C解析： -
第15题：
根据以往的生产统计，某种产品的合格率约为90%，现要求允许的估计误差不超过5%，在求置信水平为95%的置信区间时，应抽取多少个产品作为样本答案：解析：
-
第16题：
据以往的生产统计，某种产品的合格率约为90％，现要求允许的估计误差不超过5％，在求置信水平为95％的置信区间时，应抽取多少个产品作为样本答案：解析：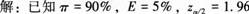
-
第17题：
某地区要对该地区的18岁以上居民进行一项抽样调查，其中有一项内容是关于居民是否获得过高等学历的调查。该项调查将采取随机数产生电话号码的电话调查方式。假定原有资料说明该地区具有高等学历人数的比例为35%。
按照原有资料该地区具有高等学历人数的比例为35%，在95%的置信度下，估计误差范围不超过0.05的情况下，应该最少抽取的样本量为（）。A．345
B．350
C．180
D．384答案：B解析： -
第18题：
从某市的居民住户中随机抽取900户，其中720户拥有电视机，在95%的置信水平下普及率为多少？在同置信水平下应抽多少居民户才保证普及率的估计误差不超过3%？
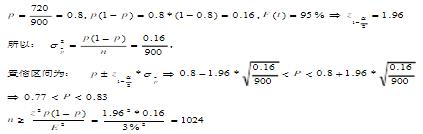
略 -
第19题：
某大型企业要提出一项改革措施，根据以往经验，职工中赞成改革的人数的比例约为50%，现在允许误差不超过3%，推断的概率保证程度为95%，至少应抽取的样本量为（）人。
- A、278
- B、652
- C、1068
- D、1112
正确答案:C -
第20题：
已知总体方差（σ^2）是144.在95%的置信水平下，为使边际误差不超过5，应选取的样本容量是（）。
- A、22
- B、23
- C、24
- D、25
正确答案:B -
第21题：
某个总体的标准差为50。从该总体中抽取100个个体作为随机样本。样本均值是600，在95%的置信水平下，边际误差是（）。
- A、5
- B、9.8
- C、650
- D、609.8
正确答案:B -
第22题：
某地区城市与郊区的人口比例为1：2，根据样本量估计的结果共需100000人估计某疾病的患病率，由于城市与郊区的患病率不同，故按城市和郊区分层随机抽样，每个层各抽取50000人，按样本中患病总人数与样本总人数之比作为样本患病率，这样可以减少偏倚。
正确答案:错误 -
第23题：
单选题某大型企业要提出一项改革措施，为了估计该城市中赞成该项改革的人数的比例，要求边际误差不超过0.03，置信水平为95%，应抽取的样本量为（）A1065
B1066
C1067
D1068
正确答案： A解析： 暂无解析
