两个自然数，它们倒数的和是1/2，这两个数是（）A、0和2B、1和1C、4和2D、3和6

题目

两个自然数，它们倒数的和是1/2，这两个数是（）

  • A、0和2
  • B、1和1
  • C、4和2
  • D、3和6
相似考题

1.一个自然数是两个合数的和，这个自然数（ ）。A 一定是合数B 一定是质数C 可能是质数也可能是合数D 以前都不是

2. 填空： （1）两个互为相反数的数（0除外）的商是 ； （2）两个互为倒数的数的积是 。

3.下列程序的功能为( )。public class Test2{public static void main(Stringargs[]){int i，s=0；for(i=1；i＜10；i+=2)s+=i+1；System.out.pnntln(s)；}}A．计算自然数1～9的累加和B．计算自然数1～10的累加和C．计算自然数1～9中的奇数之和D．计算自然数1～10中的偶数之和

4.计算机中的所有信息都是以二进制方式表示的,这两个二进制数是______。A.1和2B.0和2C.0和1D.1和10

更多“两个自然数，它们倒数的和是1/2，这两个数是（）”相关问题

  • 第1题：

    有以下程序： main() { int i,s=0; for(i=1;i＜10;i+=2) s+=i+1; ptintf("%d\n",s); } 程序执行后的输出结果是( )。

    A．自然数1～9的累加和

    B．自然数1～10的累加和

    C．自然数1～9中奇数之和

    D．自然数1～10中偶数之和


    正确答案：D
    解析：本题中，i赋初值为1，并对其每次进行加2操作，即i每次均为1～10之间的奇数，s+=i+1，即s=s+i+1，相当于s等于原来的s每次加上1～10之间的偶数，直到ilO不成立；当i=1时，s=0+1+1=2；当i=3时，s=2+3+1=2+4；当i=5时，s=2+4+5+1=2+4+6；当i=7时，s=2+4+6+7+1=2+4+6+8；当i=9时，s=2+4+6+8+9+1=2+4+6+8+10；当i=11时，i10不成立，结束循环。所以，4个选项中选项D符合题意。

  • 第2题：

    在自然数公理系统中“1”和“′”是两个没有实质意义的形式符号。()

    此题为判断题(对，错)。


    正确答案：√

  • 第3题：

    二、数学运算。通过运算。选择最合适的一项。

    请开始答题：

    26.有两个自然数，它们的和等于297，它们的最大公约数与最小公倍数之和等于693。这Nd"-自然数的差等于多少?( )

    A.33

    B．27

    C．11

    D．9


    正确答案：A

  • 第4题：

    有以下程序 main ( ) { int i,s=0; for (i=1;i＜10; i+=2) s+=i+1; print f ( "%d\n", s); } 程序执行后的输出结果是

    A．自然数1～9的累加和

    B．自然数1～10的累加和

    C．自然数1～9中奇数之和

    D．自然数1～10中偶数之和


    正确答案：D
    解析：本题考核的知识点是for循环语句和复合赋值+=运算符的应用。本题中，i赋初值为1，并对其每次进行加2操作，即i每次均为1～10之间的奇数，s+=i+1，即s=s+i+1，相当于s等于原来的s每次加上1～10之间的偶数，直到i10不成立．当i=1时，s=0+1+1=2；当i=3时，s=2+3+1=2+4；当i=5时，s=2+4+5+1=2+4+6；当i=7时，s=2+4+6+7+1=2+4+6+8；当i=9时，s=2+4+6+8+9+1=2+4+6+8+10；当i=11时，i10不成立，结束循环。所以，4个选项中选项D符合题意。

  • 第5题：

    阅读以下说明和流程图，填写流程图中的空缺，将解答填入答题纸的对应栏内。【说明】如果一个自然数N恰好等于它所有不同的真因子（即N的约数以及1，但不包括N）之和S，则称该数为“完美数”。例如6＝1＋2＋3，28＝1＋2＋4＋7＋14，所以6和28都是完美数。显然，6是第1个（即最小的）完美数。下面流程图的功能是求500以内所有的完美数。【流程图】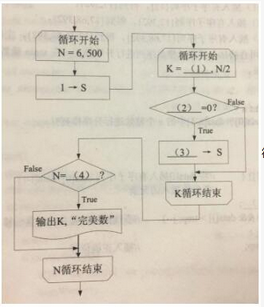

    循环开始框中要注明：循环变量＝初始值，终值［，步长］，步长为1时可以缺省。如果某自然数小于其所有真因子之和（例如24＜1＋2＋3＋4＋6＋8＋12），则称该自然数为亏数；如果某自然数大于其所有真因子之和（例如8＞1＋2＋4），则称该自然数为贏数；如果某自然数等于从1开始的若干个连续自然数之和（例如10＝1＋2＋3＋4）则称该自然数为三角形数。据此定义，自然数496是（ ）。供选择答案：A.亏数 B.赢数 C.完美数，非三角形数 D.完美数和三角形数


    答案：
    解析：
    （1）2（2）N%K（3）S+K（4）S（5）D
    【解析】

    流程图的功能是求500以内所有的完美数，N的值范围是6~500，因此N是需要判断是否为完美数，首先需要求出N的所有真因子，然后再判断N和真因子之和是否相等，从流程图可以看出S是保存真因子和的变量，K是保存真因子的变量，因此K的初始值是2，终值是N/2，因此第（1）空处填写：2；判断K是否为N的真因子，即判断N%K（N除以K取余）是否为0，第（2）空填写：N%K；当K为N的真因子时，需要计算所有K的和，即S=S+K，第（3）空填写：S+K；最后判断N和S是否相等，第（4）空填写：S。496的真因子有：1、2、4、8、16、31、62、124、248，1+2+4+8+16+31+62+124+248=496；因此496是完美数，同时496=（1+2+3+4+……+30+31），因此496是完美数和三角形数。

  • 第6题：

    有两个力作用在一个有固定转轴的刚体上：（1）这两个力都平行于轴作用时，它们对轴的合力矩一定是零；（2）这两个力都垂直于轴作用时，它们对轴的合力矩可能是零；（3）当这两个力的合力为零时，它们对轴的合力矩也一定是零；（4）当这两个力对轴的合力矩为零时，它们的合力也一定是零。在上述说法中，说法正确的是（ ）。《》（ ）

    A.只有（1）是正确的。
    B.（1）、（2）正确，（3）、（4）错误
    C.（1）、（2）、（3）都正确，（4）错误
    D.（1）、（2）、（3）、（4）都正确

    答案：B
    解析：
    力作用在一个有固定转轴的刚体上，其力矩垂直于轴作用时才能产生转动，（1）和（2）是正确的；但是，当两个力的合力为零时，它们对轴的合力矩不一定是零。同理，当这两个力对轴的合力矩为零时，它们的合力也不一定是零，所以（3）和（4）是错误的。故选B。

  • 第7题：

    三个连续的三位自然数，最小的数是9的倍数，中间的数是除以11余2，最大的数是除以15余2，求这三个连续的自然数。 （1）设最小自然数为x，满足上述条件计算机程序语言的关系表达式是（）。 A．xMod9=0Andx+1mod11=2Andx+2Mod15=2 B．xMod9=0And（x+1）mod11=2And（x+2）Mod15=2 C．Int（x/9）=0AndInt（x+1/11）=2And（x+2/15）=2 D．Int（x/9）=0AndInt（（x+1）/11）=2And（（x+2）/15）=2 （2）运用VB程序设计语言，求这三个连续的自然数，其中最小自然数x的值是（）。


    正确答案:B；540

  • 第8题：

    两个自然数，它们倒数的和是1/2，这两个数是（）

    • A、0和2
    • B、1和1
    • C、4和2
    • D、3和6

    正确答案:D

  • 第9题：

    根据两个一位二进制的加法运算规则，其和为1的正确表述为（）。

    • A、这两个二进制数都为1
    • B、这两个二进制数都为0
    • C、这两个二进制数不相等
    • D、这两个二进制数相等

    正确答案:C

  • 第10题：

    有两个力作用在一个有固定转轴的刚体上： （1）这两个力都平行于轴作用时，它们对轴的合力矩一定是零； （2）这两个力都垂直于轴作用时，它们对轴的合力矩可能是零； （3）当这两个力的合力为零时，它们对轴的合力矩也一定是零； （4）当这两个力对轴的合力矩为零时，它们的合力也一定是零． 对上述说法下述判断正确的是（）

    • A、只有（1）是正确的
    • B、（1）、（2）正确，（3）、（4）错误
    • C、（1）、（2）、（3）都正确，（4）错误
    • D、（1）、（2）、（3）、（4）都正确

    正确答案:B

  • 第11题：

    单选题
    若两个自然数的积为20，求这两个自然数和的最小值。（）
    A

    21

    B

    12

    C

    9

    D

    8


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    小明和小华计算甲、乙两个不同自然数的积（这两个自然数都比1大）。小明把较大的数字的个位数错看成了一个更大的数字，其计算结果为144，小华却把乘号看成了加号，其计算结果为28。问两个数的差为（）。
    A

    16

    B

    12

    C

    8

    D

    4


    正确答案： A
    解析： 本题适宜使用代入排除法。设两数为X与Y，依次验证选项即可，A选项验证过程如下：若X-Y=16，又由题知X+Y=28，解得：X=22，Y=6，那么如果把22的个位数看成4的话，用24×6=144，故A选项符合题意，为正确选项；若B选项，则X-Y=12，X+Y=28，解得：X=20，Y=8，那么无法将20错看成16，以得到144的积，故B选项不正确；若C选项，则X-Y=8，X+Y=28，解得：X=18，Y=10，无法将10看成8，以得到144的积，故C选项不正确；若D选项，则X-Y=4，X+Y=28，解得：X=16，Y=12，无法将16看成12，以得到144的积，故D选项不正确。所以正确选项为A选项。

  • 第13题：

    有标明数字1、2、3、4、5、6、7、9的八张卡片，将它们随意组合成两个四位数，那么这两个四位数的差值最小为（ ）。

    A．147

    B．145

    C．247

    D．109


    正确答案：A
    这两个四位数的千位数至少相差1，而要使差值尽可能小，就要使大的四位数的后三位尽可能小，小的四位数的后三位尽可能大，符合要求的只能是5123和4976，二者的差值是147。

  • 第14题：

    第五题. 推理游戏

    教授选出两个从2到9的数，把它们的和告诉学生甲，把它们的积告诉学生乙，让他们轮流猜这两个数

    甲说：“我猜不出”

    乙说：“我猜不出”

    甲说：“我猜到了”

    乙说：“我也猜到了”

    问这两个数是多少


    正确答案：

     

    第五题：3和4（可严格证明）

    　　设两个数为n1，n2，n1>=n2，甲听到的数为n=n1+n2，乙听到的数为m=n1*n2

    　　证明n1=3，n2=4是唯一解

    　　证明：要证以上命题为真，不妨先证n=7

    1)必要性：

    　　 i) n>5 是显然的，因为n<4不可能，n=4或者n=5甲都不可能回答不知道

    　　 ii) n>6 因为如果n=6的话，那么甲虽然不知道（不确定2+4还是3+3）但是无论是2，4还是3，3乙都不可能说不知道（m=8或者m=9的话乙说不知道是没有道理的）

    　　 iii) n<8 因为如果n>=8的话，就可以将n分解成 n=4+x 和 n=6+(x-2)，那么m可以是4x也可以是6(x-2)而4x=6(x-2)的必要条件是x=6即n=10，那样n又可以分解成8+2，所以总之当n>=8时，n至少可以分解成两种不同的合数之和，这样乙说不知道的时候，甲就没有理由马上说知道。

    　　 以上证明了必要性

    　　2)充分性

    　　 当n=7时，n可以分解成2+5或3+4

    　　 显然2+5不符合题

    第五题：3和4（可严格证明）

    　　设两个数为n1，n2，n1>=n2，甲听到的数为n=n1+n2，乙听到的数为m=n1*n2

    　　证明n1=3，n2=4是唯一解

    　　证明：要证以上命题为真，不妨先证n=7

    1)必要性：

    　　 i) n>5 是显然的，因为n<4不可能，n=4或者n=5甲都不可能回答不知道

    　　 ii) n>6 因为如果n=6的话，那么甲虽然不知道（不确定2+4还是3+3）但是无论是2，4还是3，3乙都不可能说不知道（m=8或者m=9的话乙说不知道是没有道理的）

    　　 iii) n<8 因为如果n>=8的话，就可以将n分解成 n=4+x 和 n=6+(x-2)，那么m可以是4x也可以是6(x-2)而4x=6(x-2)的必要条件是x=6即n=10，那样n又可以分解成8+2，所以总之当n>=8时，n至少可以分解成两种不同的合数之和，这样乙说不知道的时候，甲就没有理由马上说知道。

    　　 以上证明了必要性

    　　2)充分性

    　　 当n=7时，n可以分解成2+5或3+4

    　　 显然2+5不符合题意，舍去，容易判断出3+4符合题意，m=12，证毕

    　　于是得到n=7 m=12 n1=3 n2=4是唯一解。

    意，舍去，容易判断出3+4符合题意，m=12，证毕

    　　于是得到n=7 m=12 n1=3 n2=4是唯一解。

  • 第15题：

    下列程序的输出结果是 main( ) { int i,s=0; for(i=1;i＜10;i+=2) s+=i+1; printf(“%d\n”,s); }

    A．自然数1～9的累加和

    B．自然数1～10的累加和

    C．自然数1～9中的奇数之和

    D．自然数1～10中的偶数之和


    正确答案：D
    解析：本题执行过程：
      i  S
      ①i=1  1  s=0+1+1=2
      ②i=i+2  3  s=2+3+1=6
      ③i=i+2  5  s=6+5+1=12
      ④i=i+2  7  s=12+7+1=20
      ⑤i=i+2 9  s=20+9+1=30
      ⑥i=i+2=11＞10，循环结束。

  • 第16题：

    在1,2,3…100这100个自然数中，取两个不同的数，使得它们的和是7的倍数，共有 ( )种不同的取法。

    A．700

    B．707

    C．697

    D．705


    正确答案：B
    [答案] B。解析：100÷7=14……2。在1～100中，按被7除的余数分为了类：余1与余2的各15个，余3、余4、余5、余6、整除的各14个。取两个不同的数，要使它们的和是7的倍数，必须是：一个余1一个余6，或一个余2一个余5，或一个余3一个余4，或两个都是整除。所以，不同的取法共有15×14+15×14+14×14+14×13÷2=707。

  • 第17题：

    两个自然数的最小公倍数是351，和是66，这两个数的乘积是多少？（ ）

    A.351
    B.702
    C.1053
    D.1404

    答案：C
    解析：
    本题属于多位数问题。
    用代入排除法。将C选项1053代入可以分解为27×39，且这两个数的和为66，最小公倍数为351，符合题干。

  • 第18题：

    若两个自然数的积为20，求这两个自然数和的最小值。（）

    • A、21
    • B、12
    • C、9
    • D、8

    正确答案:C

  • 第19题：

    整数的最小公倍数是1925，这两个整数分别除以它们的最大公约数，得到2个商的和是16，这两个整数分别是：（）。


    正确答案:175和385

  • 第20题：

    小明和小华计算甲、乙两个不同自然数的积(这两个自然数都比1大)。小明把较大的数字的个位数错看成了一个更大的数字，其计算结果为144，小华却把乘号看成了加号，其计算结果为28。问两个数的差为：

    • A、16 
    • B、12 
    • C、8 
    • D、4

    正确答案:A

  • 第21题：

    有两个力作用在一个有固定转轴的刚体上：在下述说法中，（） （1）这两个力都平行于轴作用时，它们对轴的合力矩一定是零； （2）这两个力都垂直于轴作用时，它们对轴的合力矩可能是零； （3）当这两个力的合力为零时，它们对轴的合力矩也一定是零； （4）当这两个力对轴的合力矩为零时，它们的合力也一定是零。

    • A、只有（1）是正确的
    • B、（1）、（2）正确，（3）、（4） 错误
    • C、（1）、（2）、（3）都正确，（4）错误
    • D、（1）、（2）、（3）、（4）都正确.

    正确答案:B

  • 第22题：

    单选题
    有两个自然数，它们的和等于297，它们的最大公约数与最小公倍数之和等于693。这两个自然数的差等于多少？（　　）
    A

    33

    B

    27

    C

    11

    D

    9


    正确答案： C
    解析：
    设这两个数是AM、BM，M是这两个数的最大公约数，其中A、B、M均为整数。AM＋BM＝（A＋B）×M＝297，M＋A×B×M＝（1＋A×B）×M＝693，所以M是297和693的公约数。297和693的最大公约数为99。99＝32×11，把M＝1，3，9，11，33，99分别代入两个式子试算。①（A＋B）×1＝297，（1＋A×B）×1＝693，无解；②（A＋B）×3＝297，（1＋A×B）×3＝693，无解；③（A＋B）×9＝297，（1＋A×B）×9＝693，无解；④（A＋B）×11＝297，（1＋A×B）×11＝693，无解；⑤（A＋B）×33＝297，（1＋A×B）×33＝693，此时A、B一个是4，一个是5；⑥（A＋B）×99＝297，（1＋A×B）×99＝693，无解。所以⑤符合题意，当M＝33时，一个数是4×33＝132，一个数是5×33＝165，即这两个自然数的差为165－132＝33。

  • 第23题：

    单选题
    两个自然数，它们倒数的和是1/2，这两个数是（）
    A

    0和2

    B

    1和1

    C

    4和2

    D

    3和6


    正确答案： B
    解析： 暂无解析

  • 第24题：

    单选题
    两个有理数的和除以这两个有理数的积，其商为0，则这两个有理数为（　　）．
    A

    互为相反数

    B

    互为倒数

    C

    互为相反数且不为0

    D

    有一个为0


    正确答案： A
    解析：
    商为0，则分子为0，且分母不为0，所以两个数互为相反数且都不为0．

相关内容