设3阶方阵A的秩R（A）=1，则A的伴随矩阵的秩R（）等于（）．A、3B、2C、1D、0

题目

设3阶方阵A的秩R（A）=1，则A的伴随矩阵的秩R（）等于（）．

  • A、3
  • B、2
  • C、1
  • D、0
相似考题

1.设6阶方阵A的秩为3,则其伴随矩阵的秩也是3。()此题为判断题(对，错)。

2.设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则

3.设A是S×6矩阵，则( )正确。A.若A中所有5阶子式均为0，则秩R(A)=4 B.若秩R(A)=4，则A中5阶子式均为0 C.若秩R(A)=4，则A中4阶子式均非0 D.若A中存在不为0的4阶子式，则秩尺(A)=4

4.设三阶矩阵，若A的伴随矩阵的秩等于1，则必有A.a=b或a+2b=0 B.a=b或a+2b≠0 C.a≠b且a+2b=0 D.a≠b且a+2b≠0

更多“设3阶方阵A的秩R（A）=1，则A的伴随矩阵的秩R（）等于（）．”相关问题

  • 第1题：

    下列结论中正确的是（　　）。

    A、 矩阵A的行秩与列秩可以不等
    B、 秩为r的矩阵中，所有r阶子式均不为零
    C、 若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零
    D、 秩为r的矩阵中，不存在等于零的r-1阶子式

    答案：C
    解析：
    A项，矩阵A的行秩与列秩一定相等。B项，由矩阵秩的定义可知，若矩阵A（m×n）中至少有一个r阶子式不等于零，且r＜min（m，n）时，A中所有的r+1阶子式全为零，则A的秩为r。即秩为r的矩阵中，至少有一个r阶子式不等于零，不必满足所有r阶子式均不为零。C项，矩阵A的行列式不等于零意味着矩阵A不满秩，n阶矩阵的秩为n时，所对应的行列式的值大于零；当n阶矩阵的秩＜n时，所对应的行列式的值等于零。D项，秩为r的矩阵中，有可能存在等于零的r-1阶子式，如秩为2的矩阵



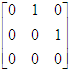
    中存在等于0的1阶子式。

  • 第2题：

    设A为m×n矩阵，B为n×m矩阵，E为m阶单位矩阵，若AB=E，则



    A.A秩r(A)=m，秩r(B)=m
    B.秩r(A)=m，秩r(B)=n
    C.秩r(A)=n，秩r(B)=m
    D.秩r(A)=n，秩r(B)=n

    答案：A
    解析：
    本题考的是矩阵秩的概念和公式.因为AB=E是m阶单位矩阵，知r(AB)=m.又因r(AB)≤min(r(A)，r(B))，故m≤r(A)，m≤r(B). ①另一方面，A是m×n矩阵，B是n×m矩阵，又有r(A)≤m，r(B)≤m. ②比较①、②得r(A)=m，r(B)=m.所以选(A)

  • 第3题：

    设A是5×6矩阵，则（ ）正确。
    A.若A中所有5阶子式均为0,则秩R(A)=4
    B.若秩R(A)=4,则A中5阶子式均为0
    C.若秩R(A)=4，则A中4阶子式均不为0
    D.若A中存在不为0的4阶子式，则秩R(A)=4


    答案：B
    解析：
    提示：利用矩阵秩的定义。

  • 第4题：

    设A是m×n矩阵，秩（A）=r＜min（m，n），则A中必（ ）

    A.至少有-r阶子式不为零，没有不等于0的r+1阶子式
    B.有等于0的r阶子式，所有r+l阶子式全为0
    C.有等于0的r阶子式，没有不等于0的r+1阶子式
    D.有等于0的r-1阶子式，有不等于0的r阶子式

    答案：A
    解析：
    由矩阵A的秩（A）=r＜min（m，n），知所有r+1阶子式全为0，r阶子式至少有一个不为0.

  • 第5题：

    设3阶矩阵，已知A的伴随矩阵的秩为1，则a=（）。

    • A、-2
    • B、-1
    • C、1
    • D、2

    正确答案:A

  • 第6题：

    单选题
    设A、B为四阶方阵，r（A）=4，r（B）=3，则r[（AB）*]=（　　）.
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： B
    解析：
    由r（A）=4，知A*是满秩矩阵，由r（B）=3，知r（B*）=1，矩阵与可逆矩阵相乘其秩不变，故有r[（AB）*]=r（B*A*）=r（B*）=1

  • 第7题：

    单选题
    设A是m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B＝AC的秩为r1，则（　　）。
    A

    r＞r1

    B

    r＜r1

    C

    r＝r1

    D

    r与r1的关系依C而定


    正确答案： A
    解析：
    由r1＝r（B）≤min[r（A），r（C）]＝r（A）＝r。
    且A＝BC－1，故r＝r（BC－1）≤min[r（B），r（C－1）]＝r（B）＝r1，所以有r＝r1。

  • 第8题：

    单选题
    设A、B都是满秩的n阶方阵，则r（AB）＝（　　）。
    A

    0

    B

    1

    C

    n－1

    D

    n


    正确答案： C
    解析：
    由行列式，|AB|＝|A|·|B|且A、B均为满秩的n阶矩阵，则有|AB|≠0，即矩阵AB满秩，故r（AB）＝n。

  • 第9题：

    单选题
    设A是m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B＝AC的秩为r1，则（　　）。
    A

    r＞r1

    B

    r＜rl

    C

    r＝rl

    D

    r与r1的关系依C而定


    正确答案： A
    解析：
    由r1＝r（B）≤min[r（A），r（C）]＝r（A）＝r。
    且A＝BC－1，故r＝r（BC－1）≤min[r（B），r（C－1）]＝r（B）＝r1，所以有r＝r1。

  • 第10题：

    单选题
    设A为4阶方阵，且r（A）＝3，A*为A的伴随矩阵，则r（A*）＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： B
    解析：
    由A是4阶方阵且r（A）＝3，知|A|＝0，又AA*＝|A|E＝0为A的齐次方程组，则A*的列向量是齐次方程组Ax(→)＝0(→)的解，故r（A）＋r（A*）≤4，则r（A*）≤1。由r（A）＝3知，A至少有一个代数余子式不为0，故A*≠0，所以r（A*）＝1。

  • 第11题：

    填空题
    设A、B都是满秩的n阶方阵，则r（AB）＝____。

    正确答案： n
    解析：
    由行列式，|AB|＝|A|·|B|且A、B均为满秩的n阶矩阵，则有|AB|≠0，即矩阵AB满秩，故r（AB）＝n。

  • 第12题：

    单选题
    下列结论中正确的是（    ）
    A

    矩阵A的行秩与列秩可以不等

    B

    秩为r的矩阵中，所有r阶子式均不为零

    C

    若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零

    D

    秩为r的矩阵中，不存在等于零的r-1阶子式


    正确答案： D
    解析：

  • 第13题：

    设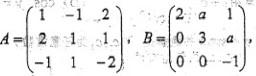则秩r(AB-A)等于：
    (A) 1(B) 2(C) 3(D)与a的取值有关


    答案：B
    解析：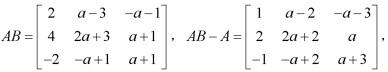
    因此r(AB-A)=2

  • 第14题：

    4阶方阵A的秩为2，则其伴随矩阵An的秩为（ ）。

    A. 0 B. 1 C. 2 D. 3


    答案：A
    解析：
    提示：A所有三阶子式为零，故An是零矩阵。

  • 第15题：

    设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（ ）.



    答案：D
    解析：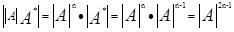

  • 第16题：

    设A是5×6矩阵，则（）正确。

    • A、若A中所有5阶子式均为0，则秩RA.=4
    • B、B.若秩R=4，则A中5阶子式均为0
    • C、C.若秩R=4，则A中4阶子式均不为0
    • D、D.若A中存在不为0的4阶子式，则秩R=4

    正确答案:B

  • 第17题：

    单选题
    设A、B都是满秩的n阶方阵，则r（AB）＝（　　）。
    A

    n－1

    B

    n

    C

    n＋1

    D

    n＋2


    正确答案： A
    解析：
    由行列式，|AB|＝|A|·|B|且A、B均为满秩的n阶矩阵，则有|AB|≠0，即矩阵AB满秩，故r（AB）＝n。

  • 第18题：

    单选题
    设3阶方阵A的秩R（A）=1，则A的伴随矩阵的秩R（）等于（）．
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： B
    解析： 暂无解析

  • 第19题：

    单选题
    设A是5×6矩阵，则（）正确。
    A

    若A中所有5阶子式均为0，则秩RA.=4

    B

    B.若秩R=4，则A中5阶子式均为0

    C

    C.若秩R=4，则A中4阶子式均不为0

    D

    D.若A中存在不为0的4阶子式，则秩R=4


    正确答案： C
    解析： 暂无解析

  • 第20题：

    填空题
    设A为4阶方阵，且r（A）＝3，A*为A的伴随矩阵，则r（A*）＝____。

    正确答案： 1
    解析：
    由A是4阶方阵且r（A）＝3，知|A|＝0，又AA*＝|A|E＝0为A的齐次方程组，则A*的列向量是齐次方程组Ax(→)＝0(→)的解，故r（A）＋r（A*）≤4，则r（A*）≤1。由r（A）＝3知，A至少有一个代数余子式不为0，故A*≠0，所以r（A*）＝1。

  • 第21题：

    单选题
    设3阶矩阵，已知A的伴随矩阵的秩为1，则a=（）。
    A

    -2

    B

    -1

    C

    1

    D

    2


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    设A为3阶方阵，α(→)1，α(→)2，α(→)3是互不相同的3维列向量，且都不是方程组Ax(→)＝0(→)的解，若B＝（α(→)1，α(→)2，α(→)3）满足r（AB）＜r（A），r（AB）＜r（B），则r（AB）等于（　　）。
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： C
    解析：
    由于α(→)1，α(→)2，α(→)3不是Ax(→)＝0(→)的解，故AB≠0，所以r（AB）＞0。
    又因r（AB）＜r（A），故B不可逆，即r（B）≤2，从而r（AB）＜r（B）≤2，即r（AB）＝1。

  • 第23题：

    单选题
    设A、B都是4阶方阵且AB＝0，则r（A）＋r（B）（　　）。
    A

    ≤1

    B

    ≤2

    C

    ≤3

    D

    ≤4


    正确答案： C
    解析：
    由AB＝0，知矩阵B的列向量是方程组AX(→)＝0(→)的解，令r（A）＝r1，r（B）≤4－r1，故r（A）＋r（B）≤4。

相关内容