求多项式A（x）的算法可根据下列两个公式之一来设计：⑴A（x）=anxn+an-1xn-1+…+a1x+a0⑵A（x）=（…（anx+an-1）x+…+a1）x）+a0根据算法的时间复杂度分析比较这两种算法的优劣。

题目

求多项式A（x）的算法可根据下列两个公式之一来设计：⑴A（x）=anxn+an-1xn-1+…+a1x+a0⑵A（x）=（…（anx+an-1）x+…+a1）x）+a0根据算法的时间复杂度分析比较这两种算法的优劣。

相似考题

1.要发送的数据为101110。采用CRC的生成多项式是P(x)=x3＋1。试求应添加在数据后面的余数(冗余码)____________。

2.在Z3={0,1,2}中,求一个多项式f(x)使得f(1)=0,f(2)=0。

3.若在[a,b]上用Ln(x)近似f(x)，则其截断误差为Rn(x)=f(x)-Ln(x)，也称为插值多项式的()A、余项B、插值公式C、插值多项式D、以上都不对

4.要发送的数据为101110101，采用CRC的生成多项式是P(x)=x4+x+1，试求该添加在数据后的余数以及发送序列是多少?

参考答案和解析
正确答案:第二种算法的时间性能要好些。第一种算法需执行大量的乘法运算，而第二种算法进行了优化，减少了不必要的乘法运算。
更多“求多项式A（x）的算法可根据下列两个公式之一来设计：⑴A（x）=”相关问题

  • 第1题：

    发送方准备发送的信息位为1010101，采用CRC校验算法，生成多项式G(x)=X4+X3+X2+1，发出的校验位为()

    A、0110

    B、1001

    C、1010

    D、0101


    参考答案：B

  • 第2题：

    一道数学题为“已知P,Q为两个多项式，请计算2P+Q”，粗心的小明在解题时，将“2P+Q”误看成“P+2Q”，求得的结果为9x2+2x+9，已知Q=x2+3x-2。
    (1)求这道数学题的正确答案；(4分)
    (2)若P=6Q，求x的值。(4分)


    答案：
    解析：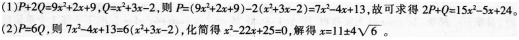

  • 第3题：

    若要传输的数据M=1010001101，生成多项式为P（X）=X5+X4+X2+1，求CRC码的检验序列码，并验证收到的码字101000110101110的正确性。


    正确答案: C.RC码的检验序列码为：01110。
    收到的码字101000110101110是正确的。

  • 第4题：

    一个次数大于0的本原多项式g（x）在Q上可约，那么g（x）可以分解成两个次数比g（x）次数低的本原多项式的乘积。


    正确答案:正确

  • 第5题：

    设输入的信息码字为1101001，预先约定的生成多项式为：G（x）=X4＋X3＋X2＋1请用长除法求出传送多项式T（x）及其相应的发送代码。


    正确答案: 被除数为信息码后面加0000，即11010010000，由生成多项式得除数为11101
    11010010000÷11101得余数0000发送码字为信息码字加余数，
    即1101010000生成多项式为：T（X）=X10＋X9＋X7＋X4

  • 第6题：

    f（x）（系数为an…a0）是一个次数n>0的本原多项式，q/p是有理根，那么可以得到f（x）=（px-q）g（x）成立，那么g（x）是什么多项式？（）

    • A、任意多项式
    • B、非本原多项式
    • C、本原多项式
    • D、无理数多项式

    正确答案:C

  • 第7题：

    单选题
    两个本原多项式g（x）和h（x）若在Q[x]中相伴，那么g（x）/h（x）等于多少？（）
    A

    ±1

    B

    任意常数c

    C

    任意有理数

    D

    任意实数


    正确答案： C
    解析： 暂无解析

  • 第8题：

    单选题
    一个次数大于0的整系数多项式f（x）在Q上可约，那么f（x）可以分解成两个次数比f（x）次数低的什么多项式的乘积。（）
    A

    整系数多项式

    B

    本原多项式

    C

    复数多项式

    D

    无理数多项式


    正确答案： B
    解析： 暂无解析

  • 第9题：

    问答题
    求多项式A（x）的算法可根据下列两个公式之一来设计：⑴A（x）=anxn+an-1xn-1+…+a1x+a0⑵A（x）=（…（anx+an-1）x+…+a1）x）+a0根据算法的时间复杂度分析比较这两种算法的优劣。

    正确答案： 第二种算法的时间性能要好些。第一种算法需执行大量的乘法运算，而第二种算法进行了优化，减少了不必要的乘法运算。
    解析： 暂无解析

  • 第10题：

    单选题
    两个本原多项式g（x）和f（x），令h（x）=g（x）f（x）记作Cs，若h（x）不是本原多项式，则存在p当满足什么条件时使得p|Cs（s=0，1…）成立？（）
    A

    p是奇数

    B

    p是偶数

    C

    p是合数

    D

    p是素数


    正确答案： D
    解析： 暂无解析

  • 第11题：

    单选题
    不可约多项式f（x）的因式有哪些？（）
    A

    只有零次多项式

    B

    只有零次多项式和f（x）的相伴元

    C

    只有f（x）的相伴元

    D

    根据f（x）的具体情况而定


    正确答案： A
    解析： 暂无解析

  • 第12题：

    问答题
    要发送的数据为101110。采用CRCD 生成多项式是P（X）=X3+1。试求应添加在数据后面的余数？

    正确答案： 作二进制除法，10111000010011添加在数据后面的余数是011
    解析： 暂无解析

  • 第13题：

    若使用生成多项式G(x)=1011,求有效信息1100的CRC码


    答案：101

  • 第14题：

    二元多项式f（x1,x2)，如果将x1，x2对换后，有f(x1,x2=f(x2,x1)则称f（x1,x2）为二元对称多项式。下列是二元对称多项式的是( )。
    A．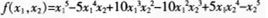
    B．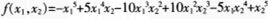
    C．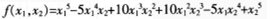
    D．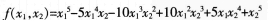


    答案：C
    解析：
    由定义，互换石。，石：的位置，二元多项式不变，即正确选项为选项C。

  • 第15题：

    在CRC码计算中，可以将一个二进制位串与一个只含有0或1两个系数的多项式建立对应关系。与位串101110对应的多项式为（）。

    • A、X6+X4+X3+1
    • B、X5+X3+X2+1
    • C、X5+X3X2+X
    • D、X6+X5+X4+1

    正确答案:C

  • 第16题：

    不可约多项式f（x）的因式有哪些？（）

    • A、只有零次多项式
    • B、只有零次多项式和f（x）的相伴元
    • C、只有f（x）的相伴元
    • D、根据f（x）的具体情况而定

    正确答案:B

  • 第17题：

    要发送的数据为101110。采用CRCD 生成多项式是P（X）=X3+1。试求应添加在数据后面的余数？


    正确答案: 作二进制除法，10111000010011添加在数据后面的余数是011

  • 第18题：

    两个本原多项式g（x）和h（x）若在Q[x]中相伴，那么g（x）/h（x）等于多少？（）

    • A、±1
    • B、任意常数c
    • C、任意有理数
    • D、任意实数

    正确答案:A

  • 第19题：

    判断题
    一个次数大于0的本原多项式g（x）在Q上可约，那么g（x）可以分解成两个次数比g（x）次数低的本原多项式的乘积。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第20题：

    单选题
    f（x）（系数为an…a0）是一个次数n>0的本原多项式，q/p是有理根，那么可以得到f（x）=（px-q）g（x）成立，那么g（x）是什么多项式？（）
    A

    任意多项式

    B

    非本原多项式

    C

    本原多项式

    D

    无理数多项式


    正确答案： D
    解析： 暂无解析

  • 第21题：

    单选题
    已知两点(2,4)、(4,6),利用插值多项式求点(3,x)中的x为（　）。
    A

    4.5

    B

    5.0

    C

    4.75

    D

    5.5


    正确答案： A
    解析： 暂无解析

  • 第22题：

    问答题
    设输入的信息码字为1101001，预先约定的生成多项式为：G（x）=X4＋X3＋X2＋1请用长除法求出传送多项式T（x）及其相应的发送代码。

    正确答案： 被除数为信息码后面加0000，即11010010000，由生成多项式得除数为11101
    11010010000÷11101得余数0000发送码字为信息码字加余数，
    即1101010000生成多项式为：T（X）=X10＋X9＋X7＋X4
    解析： 暂无解析

  • 第23题：

    单选题
    两个本原多项式g（x）和h（x）若在Q[x]中相伴，那么有什么等式成立？（）
    A

    g（x）=h（x）

    B

    g（x）=-h（x）

    C

    g（x）=ah（x）（a为任意数）

    D

    g（x）±h（x）


    正确答案： B
    解析： 暂无解析

相关内容