若已知某二叉树的中序和后序遍历序列分别BCAEFD和CBFEDA，则该二叉树的先序序列为（）。A、ABCDEFB、ABDCEFC、ABDCFED、ACBDFE

题目

若已知某二叉树的中序和后序遍历序列分别BCAEFD和CBFEDA，则该二叉树的先序序列为（）。

  • A、ABCDEF
  • B、ABDCEF
  • C、ABDCFE
  • D、ACBDFE
相似考题

1.● 已知一个二叉树的先序遍历序列为①、②、③、④、⑤，中序遍历序列为②、①、④、③、⑤，则该二叉树的后序遍历序列为 （57） 。对于任意一棵二叉树，叙述错误的是 （58） 。（57）A. ②、③、①、⑤、④B. ①、②、③、④、⑤C. ②、④、⑤、③、①D. ④、⑤、③、②、①（58）A. 由其后序遍历序列和中序遍历序列可以构造该二叉树的先序遍历序列B. 由其先序遍历序列和后序遍历序列可以构造该二叉树的中序遍历序列C. 由其层序遍历序列和中序遍历序列可以构造该二叉树的先序遍历序列D. 由其层序遍历序列和中序遍历序列不能构造该二叉树的后序遍历序列

2.已知一个二叉树的先序遍历序列为①、②、③、④、⑤，中序遍历序列为②、①、④、③、⑤，则该二叉树的后序遍历序列为( )。对于任意一棵二叉树，叙述错误的是( )。A．②、③、①、⑤、④B．①、②、③、④、⑤C．②、④、⑤、③、①D．④、⑤、③、②、①

3.若二叉树的先序遍历序列为ABCEDF，后序遍历序列为CEBFDA，则其中序遍历序列为(65)。A．CEFBDAB．CBEAFDC．CEBAFDD．CBEDFA

4.若二叉树的先序遍历序列为ABDECF，中序遍历序列DBEAFC，则其后序遍历序列为(40)。A．DEBAFCB．DEFBCAC．DEBCFAD．DEBFCA

更多“若已知某二叉树的中序和后序遍历序列分别BCAEFD和CBFEDA，则该二叉树的先序序列为（）。A、ABCDEFB、ABDCEFC、ABDCFED、ACBDFE”相关问题

  • 第1题：

    若已知一棵二叉树先序序列为ABCDEFG,中序序列为CBDAEGF,则其后序序列为()。

    :ACDBGFEA

    BCDBFGEA

    CCDBAGFE

    DBCDAGFE


    参考答案：A

  • 第2题：

    一棵二叉树的先序遍历序列为ABCDEF,中序遍历序列为CBAEDF,则后序遍历序列为()。

    A.CBEFDA

    B.FEDCBA

    C.CBEDFA

    D.不确定


    参考答案：A

  • 第3题：

    已知某二叉树的先序遍历序列是ABDCE，中序遍历序列是BDAEC，则该二叉树为______。

     


    正确答案：C
    解析：本题考查数据结构基础知识。
    对二叉树进行先序遍历的过程是：若二叉树非空，则先访问根结点，然后先序遍历左子树，最后先序遍历右子树。因此，二叉树的先序遍历序列中，第一个元素是根结点。
      对二叉树进行中序遍历的过程是：若二叉树非空，则先中序遍历左子树，然后访问根结点，最后中序遍历右子树。因此，若在中序遍历序列中已找出二叉树的根结点，则根结点左边为左子树的中序遍历序列，右边是右子树的中序遍历序列。
      由此，根据先序序列确定根结点，根据中序序列划分左右子树，反复应用此原则，就可根据先序遍历序列和中序遍历序列恢复二叉树的结构。
      本题中，先序序列为ABDCE，因此A是树根结点，中序序列为BDAEC，因此BD是左子树上的结点，EC是右子树上的结点。根据先序遍历序列，可知B是左子树的根结点，C是右子树的根结点。在中序遍历序列BDAEC中，D在B之后，因此D是B的右孩子。同理，在中序遍历序列BDAEC中，E在C之前，因此E是C的左孩子。

  • 第4题：

    若二叉树的先序遍历序列为ABDECF，中序遍历序列DBEAFC，则其后序遍历序列为______。

    A．DEBAFC

    B．DEFBCA

    C．DEBCFA

    D．DEBFCA


    正确答案：D

  • 第5题：

    若某二叉树的先序遍历序列和中序遍历序列分别为PBECD、BEPCD，则该二叉树的后序遍历序列为(39)。

    A．PBCDE

    B．DECBP

    C．EBDCP

    D．EBPDC


    正确答案：C

  • 第6题：

    ●已知某二叉树的先序遍历序列为ABCD，中序遍历序列为BADC，则该二叉树的后序遍历序列为(39)。

    (39)A.BDCA

    B.CDBA

    C.DBCA

    D.BCDA


    正确答案：A

  • 第7题：

    已知某二叉树的先序遍历序列为ABCD，后序遍历序列为CDBA，则该二叉树为( )。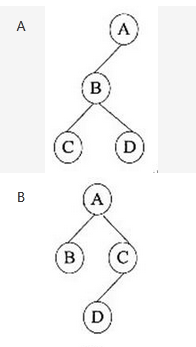



    答案：A
    解析：
    本题考查数据结构基础知识。
    对非空的二叉树进行先序遍历的过程是：先访问根结点，然后先序遍历左子树，最后先序遍历右子树。题中四个二叉树的先序遍历序列分别为ABCD、ABCD、ABCD、ACBD。
    对非空的二叉树进行后序遍历的过程是：先后序遍历左子树，接着后序遍历右子树，最后再访问根结点。题中四个二叉树的后序遍历序列分别为CDBA、BDCA、DCBA、DBCA。

  • 第8题：

    —棵二叉树的后序遍历序列为DABEC，中序遍历序列为DEBAC，则先序遍历序列为()。

    A.ACBED
    B.DECAB
    C.DEABC
    D.CEDBA

    答案：D
    解析：
    由后序序列必定最后一个访问根结点，故C为根结点。在先序遍历中首先访问根结点C。

  • 第9题：

    若二叉树的先序遍历序列为ABDECF，中序遍历序列DBEAFC，则其后序遍历序列为（）

    • A、DEBAFC
    • B、DEFBCA
    • C、DEBCFA
    • D、DEBFCA

    正确答案:D

  • 第10题：

    假设一棵二叉树的先序序列为EBADCFHGIKJ，中序序列为ABCDEFGHIJK，请写出该二叉树的后序遍历序列。


    正确答案:后序序列：ACDBGJKIHFE

  • 第11题：

    单选题
    若已知某二叉树的中序和后序遍历序列分别BCAEFD和CBFEDA，则该二叉树的先序序列为（）。
    A

    ABCDEF

    B

    ABDCEF

    C

    ABDCFE

    D

    ACBDFE


    正确答案： D
    解析： 暂无解析

  • 第12题：

    问答题
    已知某二叉树的先序遍历序列是aecdb，中序遍历序列是eadcb。给出上述二叉树的后序遍历序列。

    正确答案： edbca
    解析： 暂无解析

  • 第13题：

    若二叉树的先序遍历序列为ABDECF，中序遍历序列为DBEAFC，则其后序遍历序列为(8)。

    A．DEBAFC

    B．DEFBCA

    C．DEBCFA

    D．DEBFCA


    正确答案：D
    解析：本题要求根据二叉树的先序遍历和中序遍历求后序遍历。我们可以根据这棵二叉树的先序和中序遍历画出这棵二叉树，然后再得出其后序遍历结果。根据先序和中序来构造二叉树的规则是这样的：首先看先序遍历序列ABDECF，先序遍历中第一个访问的结点是A，这说明A是二叉树的根结点(因为先序遍历顺序是：根，左，右)。然后看中序遍历序列DBEAFC，中序中A前面有结点DBE，后面有结点FC。这说明DBE是A的左子树，FC是A的右子树(因为中序遍历顺序是：左，根，右)。再回到先序遍历序列中看DBE的排列顺序(此时可以不看其他的结点)，我们发现在先序遍历序列中B排在最前面，所以B是A的左子树的根结点。接下来又回到了中序遍历序列，中序遍历序列中D在B的前面，E在B的后面，所以D是B的左子树，E是B的右子树。对于A的右子树，可同样依此规则得出。由此，可构造二叉树，如图4-8所示。然后对这棵二叉树进行后序遍历，得到DEBFCA。

  • 第14题：

    若某二叉树的前序遍历序列和中序遍历序列分别为PBECD、BEPCD，则该二叉树的后序遍历序列为 ____ 。

    A．PBCDE

    B．DECBP

    C．EBDCP

    D．EBPDC

    A．

    B．

    C．

    D．


    正确答案：C

  • 第15题：

    若某二叉树的后序遍历序列为KBFDCAE，中序遍历序列为BKEFACD，则该二叉树为 （58）。

    A.A

    B.B

    C.C

    D.D


    正确答案：A
    本题考查二叉树的遍历。二叉树的主要遍历方式有：前序遍历、中序遍历、后序遍历、层次遍历。如果已知中序遍历，并知道前序遍历与后序遍历中的任意一个，便可得到一棵唯一的二叉树。具体是怎么做的呢？利用的是遍历的特点。中序遍历的顺序是：左、根、右。而后序遍历的顺序是：左、右、根。回到题目里面来，从“后序遍历序列为KBFDCAE”，可以得知，二叉树的根结点为：E（此时已经可以排除选项C与选项D了）。继续分析，由“中序遍历序列为BKEFACD”，可以得知，二叉树的左子树包括结点：BK。右子树包括结点：FACD。重复上面的步骤，对左子树与左子树看成独立的两棵树进行分析。在后序遍历中，左子树的结点BK的顺序为“KB”，所以B是根结点；右子树的结点FACD的顺序为“FDCA”，所以右子树的根结点为A。当分析到这一步时，已经可以得到本题答案为A。

  • 第16题：

    已知某二叉树的中序、层序序列分别为DBAFCE，FDEBCA，则该二叉树的后序序列为(7)。

    A．BCDEAF

    B．ABDCEF

    C．DBACEF

    D．DABECF


    正确答案：B
    解析：按照遍历左子树要在遍历右子树之前进行的原则，根据访问根节点位置的不同，可得到二叉树的前序、中序和后序3种遍历方法。层序遍历是从根节点(第1层)出发，首先访问第1层的树根节点，然后从左到右依次访问第2层上的节点，再次是第三层上的节点，依次类推，自上而下、自左向右逐层访问各层上的节点。对二叉树而言，第n层节点最多为2n-1。由层序序列可得；F是树根节点，D，E是第2层节点；结合中序序列有DBA构成F的左子树，CE构成F的右子树，进一步有C是E的左节点，E无右节点；这样A是第4层节点，据DBA序列有B是D的右节点，A是B的右节点。由此易知后序序列为ABDCEF。

  • 第17题：

    己知某二叉树的先序遍历序列为ABCD，后序遍历序列为CDBA，则该二叉树为 (40)。

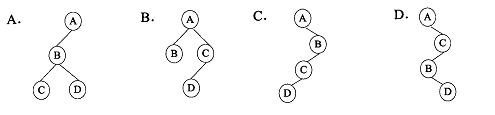
    A.A

    B.B

    C.C

    D.D


    正确答案：A
    本题考查数据结构基础知识。对非空的二叉树进行先序遍历的过程是：先访问根结点，然后先序遍历左子树，最后先序遍历右子树。题中四个二叉树的先序遍历序列分别为ABCD、ABCD、ABCD、ACBD.对非空的二叉树进行后序遍历的过程是：先后序遍历左子树，接着后序遍历右子树，最后再访问根结点。题中四个二叉树的后序遍历序列分别为CDBA、BDCA．DCBA、DBCA.

  • 第18题：

    已知二叉树的中序序列和后序序列均为ABCDEF，则该二叉树的先序序列为 ( )

    A．FEDCBA

    B．ABCDEF

    C．FDECBA

    D．FBDCEA


    正确答案：A
    解析：对于前序遍历、中序遍历和后序遍历，将结点按其访问的先后次序排列起来，所得到的结点序列分别称为前序序列、中序序列和后序序列。

  • 第19题：

    已知某二叉树的中序、层序序列分别为DBAFCE、FDEBCA，则该二叉树的后序序列为()。

    A.DBACEF
    B.DABECF
    C.BCDEAF
    D.ABDCEF

    答案：D
    解析：
    按照遍历左子树要在遍历右子树之前进行的原则，根据访问根节点位置的不同，可得到二叉树的前序，中序和后序3种遍历方法。层序遍历是从根节点(第1层)出发，首先访问第1层的树根节点，然后从左到右依次访问第2层上的节点，其次是第3层上的节点，依此类推，自上而下，自左向右逐层访问各层上的节点。对于二叉树来说，第n层节点最多为2m1。由层序序列可得: F是树根节点，D. E是第2层节点:结合中序序列有DBA构成F的左子树，CE构成F的右子树，进-一步有C是E的左节点、B无右节点:这样A是第4层节点，据DBA序列有B是D的右节点. A是B的右节点。易知后序序列为ABDCEF.

  • 第20题：

    已知某二叉树的先序遍历序列是aecdb，中序遍历序列是eadcb。给出上述二叉树的后序遍历序列。
    edbca
    略

  • 第21题：

    某二叉树的中序遍历序列为：DEBAC，后序遍历序列为：EBCAD。则前序遍历序列为（）。


    正确答案:DABEC

  • 第22题：

    单选题
    若已知一棵二叉树先序序列为ABCDEFG，中序序列为CBDAEGF，则其后序序列为（）
    A

    CDBGFEA

    B

    CDBFGEA

    C

    CDBAGFE

    D

    BCDAGFE


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    若某二叉树的前序遍历序列为ABDCEFG，中序遍历序列为DBCAFEG，则其后序遍历序列为（）。
    A

    DCBFGEA

    B

    DCBAFGE

    C

    GFCDEBA

    D

    DCFGBEA


    正确答案： A
    解析： 暂无解析

相关内容