除了简单线性回归模型的基本假设条件，多元回归模型还应满足的假设是（）A、误差项u的数学期望值为0B、误差的方差为一常量C、各项误差之间不存在相关关系D、自变量间不存在相关关系

题目

除了简单线性回归模型的基本假设条件，多元回归模型还应满足的假设是（）

  • A、误差项u的数学期望值为0
  • B、误差的方差为一常量
  • C、各项误差之间不存在相关关系
  • D、自变量间不存在相关关系
相似考题

1.线性回归的基本假设不包括哪个()A.随机误差项是一个期望值为0的随机变量B.对于解释变量的所有观测值，随机误差项有相同的方差C.随机误差项彼此相关D.解释变量是确定性变量不是随机变量，与随机误差项之间相互独立E.随机误差项服从正态分布

2.当线性回归模型的相关系数r=0时,说明自变量与因变量之间()。A、不存在线性关系B、存在其他关系C、一定没有任何关系D、存在线性关系

3.（ ）是指模型的误差项间存在相关性。 A、异方差 B、自相关 C、伪回归 D、多重共线性

4.对于简单线性回归模型的假设条件，下列哪一种说法不正确（）A.误差项是一个独立的随机变量B.误差项的期望值等于0C.误差项的方差可以不同D.误差项为正太分布

更多“除了简单线性回归模型的基本假设条件，多元回归模型还应满足的假设是（）A、误差项u的数学期望值为0B、误差的方差为一常量C、各项误差之间不存在相关关系D、自变量间不存在相关关系”相关问题

  • 第1题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项μi的基本假设是（ ）。
    Ⅰ.随机项μi自变量的任一观察值xi不相关
    Ⅱ.E（μi）=0，V（μi）=σμ^2=常数
    Ⅲ.线每个μi为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A.Ⅰ.Ⅱ.Ⅲ
    B.Ⅰ.Ⅱ.Ⅲ.Ⅳ
    C.Ⅱ.Ⅲ.Ⅳ
    D.Ⅰ.Ⅲ.Ⅳ

    答案：B
    解析：
    一元线性回归模型为：yi=α十βxi+μi，（i=1，2，3，....），其中yi为被解释变量；xi为解释变量；μi是一个随机变量，称为随机项。随机项μi满足如下基本假定：①每个μi均为独立同分布，服从正态分布的随机变量，且E（μi）=0，V（μi）=σμ∧2=常数；②每个随机项μi均互不相关，即：Cov（μi，μj）=0 （i≠j）；③随机项μi与自变量的任一观察值xi不相关，即：Cov（μi，xi）=0 （i=1，2，3，...，n）。

  • 第2题：

    回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）
    Ⅰ.被解释变量与解释变量之间具有线性关系
    Ⅱ.随机误差项服从正态分布
    Ⅲ.各个随机误差项的方差相同
    Ⅳ.各个随机误差项之间不相关

    A：Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B：Ⅰ.Ⅲ.Ⅳ
    C：Ⅰ.Ⅱ.Ⅳ
    D：Ⅱ.Ⅲ.Ⅳ

    答案：A
    解析：
    —元线性回归模型为：yi=a+βi+mi（i=l,2,3,*,n）,其中yi为解解释变量Xi为解释变量;ui是一个随机变垦量.称为随机项。要求随机项u和自变量，Xi满足的统计假定如下：①每个ui均为独立同分右（IID、）,服从正态分右的随机变量，E（ui）=0,V（ui）=σ＾2常数②随机项ui与自变量的任一观察值Xi不相关，即COV（ui,i）=0

  • 第3题：

    （　　）是指模型的误差项间存在相关性。

    A.异方差
    B.自相关
    C.伪回归
    D.多重共线性

    答案：B
    解析：
    自相关是指模型的误差项间存在相关性。一旦发生自相关，则意味着数据中存在自变量所没有解释的某种形态，说明模型还不够完善。考试精准押题，瑞牛题库软件考前更新，下载链接 www.niutk.com

  • 第4题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项i的基本假设是（ ）。
    Ⅰ.随机项i与自变量的任一观察值Xi不相关
    Ⅱ. E(i)=0,V(i)=σ2=常数
    Ⅲ.每个i均为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A、Ⅰ.Ⅱ.Ⅲ
    B、Ⅰ.Ⅱ.Ⅲ.Ⅳ
    C、Ⅱ.Ⅲ.Ⅳ
    D、Ⅰ.Ⅱ.Ⅳ


    答案：B
    解析：

  • 第5题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假硅是( )。

    A: 被解释变量与解释变量之间具有线性关系
    B: 随机误差项服从止态分布
    C: 并个随机误差项的方差相同
    D: 并个随机误差项之叫不相关

    答案：A,B,C,D
    解析：

  • 第6题：

    如果线性回归模型中随机误差项的方差不是（），则称随机误差项具有异方差性。


    正确答案:常数

  • 第7题：

    简单线性回归模型与多元回归模型的基本假设（）

    • A、完全相同
    • B、除了有相同的条件外，后者比前者少
    • C、除了有相同的条件外，后者比前者多
    • D、没有关系

    正确答案:C

  • 第8题：

    多选题
    A

    因变量与自变量之间的关系为线性关系

    B

    随机误差项的均值为l

    C

    随机误差项之间是不独立的

    D

    随机误差项的方差是常数


    正确答案： A,D
    解析：

  • 第9题：

    多选题
    多元回归模型的基本假设条件有（）
    A

    误差项u的数学期望值为0

    B

    误差的方差为一常量

    C

    误差的标准差为一常量

    D

    各项误差之间不存在相关关系

    E

    自变量之间不存在相关关系<br />


    正确答案： C,B
    解析： 暂无解析

  • 第10题：

    不定项题
    A

    因变量与自变量之间的关系为线性关系

    B

    随机误差项的均值为1

    C

    随机误差项之间是不独立的

    D

    随机误差项的方差是常数


    正确答案： B
    解析：

  • 第11题：

    单选题
    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是()。 I 被解释变量与解释变量之间具有线性关系 Ⅱ 随机误差项服从正态分布 Ⅲ 各个随机误差项的方差相同 Ⅳ 各个随机误差项之间不相关
    A

    I、Ⅱ、Ⅲ

    B

    I、Ⅲ、Ⅳ

    C

    Ⅱ、Ⅲ、Ⅳ

    D

    I、Ⅱ、Ⅲ、Ⅳ


    正确答案： D
    解析： 一元线性回归模型为：Yi=α+βxi+ui，(i=1，2，3，…，n)，其中Yi为被解释变量，xi为解释变量，ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E(ui)=0，V(ui)=σ2=常数；②随机项ui与自变量的任一观察值xi不相关，即Cov(ui，xi)=0．

  • 第12题：

    多选题
    多元线性回归分析是建立在哪些假设基础上的？（　　）
    A

    解释变量之间不存在线性关系

    B

    自变量x1，x2，…，xk是随机变量

    C

    所有随机误差项μ的均值为1

    D

    所有随机误差项μ服从正态分布N（0，σ2）


    正确答案： C,A
    解析：
    多元线性回归模型满足如下基本假定：
    ①零均值假定，即E（μi）＝0（i＝1，2，…，n）；
    ②同方差与无自相关假定，即随机扰动项的方差和协方差满足：
    Var（μi）＝σ2＝常数（i＝1，2，…，n）
    Cov（μi，μj）＝0（i≠j）
    ③无多重共线性假定，即解释变量之间不存在线性关系；
    ④随机扰动项与解释变量互不相关，即：Cov（μi，xji）＝0（i＝1，2，…，n；j＝1，2，…，k）；
    ⑤正态性假定，随机扰动项μi服从正态分布，即μi～N（0，σ2）。

  • 第13题：

    回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）
    Ⅰ.被解释变量与解释变量之间具有线性关系
    Ⅱ.随机误差项服从正态分布
    Ⅲ.各个随机误差项的方差相同
    Ⅳ.各个随机误差项之间不相关

    A.Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B.Ⅰ.Ⅲ.Ⅳ
    C.Ⅰ.Ⅱ.Ⅳ
    D.Ⅱ.Ⅲ.Ⅳ

    答案：A
    解析：
    —元线性回归模型为：yi=a+βi+mi（i=l,2,3,*,n）,其中yi为解解释变量Xi为解释变量;ui是一个随机变垦量.称为随机项。要求随机项u和自变量，Xi满足的统计假定如下：①每个ui均为独立同分右（IID、）,服从正态分右的随机变量，E（ui）=0,V（ui）=σ＾2常数②随机项ui与自变量的任一观察值Xi不相关，即COV（ui,i）=0

  • 第14题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型早回归分析的基础。线性回归模型中关于随机项μi的基本假设是（ ）。
    Ⅰ.随机项μi与自变量的任一观察值xi不相关=常数
    Ⅱ.
    Ⅲ.每个μi均为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A、Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B、Ⅰ.Ⅱ.Ⅲ
    C、Ⅰ.Ⅱ.Ⅳ
    D、Ⅱ.Ⅲ.Ⅳ


    答案：A
    解析：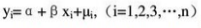
    一元线性回归模型为:，其中yi为被解释变量；xi为解释变量；μi是一个随机变量，称为随机项。随机项μi满足如下基本假定:①每个μi均为独立同分布，服从正态分布的随机变量，且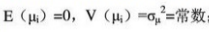；②每个随机相Ri均互不相关，即；③随机项Ri与自变量的任一观察值xi不相关,即: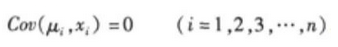


  • 第15题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）。
    I 被解释变量与解释变量之间具有线性关系
    Ⅱ 随机误差项服从正态分布
    Ⅲ 各个随机误差项的方差相同
    Ⅳ 各个随机误差项之间不相关

    A.I、Ⅱ、Ⅲ
    B.I、Ⅲ、Ⅳ
    C.Ⅱ、Ⅲ、Ⅳ
    D.I、Ⅱ、Ⅲ、Ⅳ

    答案：D
    解析：
    一元线性回归模型为：Yi=α+βxi+ui，(i=1，2，3，…，n)，其中Yi为被解释变量，xi为解释变量，ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E(ui)=0， V(ui)=σ2=常数；②随机项ui与自变量的任一观察值xi不相关，即Cov(ui，xi)=0．

  • 第16题：

    根据线性回归模型的基本假定，随机误差项应是随机变量，且满足( )。

    A: 自相关性
    B: 异方差性
    C: 与被解释变量不相关
    D: 与解释变量不相关

    答案：D
    解析：

  • 第17题：

    一元线性回归分析是建立在一系列假设基础上的，这些假设包括对于自变量x的假设，以及对随机误差项C的假设，包括( )。

    A: 因变量B．自变量之间具有线性关系
    B: 自变量是随机的
    C: 误差项的方差为0。
    D: 误差项是独立随机变量且服从止态分布

    答案：A,D
    解析：
    一般地，在作一元线性回归分析过程巾，回归分析是建立-系列假设基础上的，
    这些假设为：①因变量y于自变量x之间具有线性关系；②在重复抽样巾，自变量x的取值是固定的，即假定x是非随机的，③随机误差顶c的均值为零，方差为常数，④随机误差项c的方差为常数：⑤随机误差项μ 之刚是独立随机变量且服从正态分布，即,μ ~N (O,?)。

  • 第18题：

    一般地，在一元线性回归分析过程中，回归分析是建立一系列假设基础上的，这些假设为（）

    • A、回归模型因变量Y与自变量x之间具有线性关系。
    • B、在重复抽样中，自变量x的取值是固定的，即假定x是非随机的。
    • C、误差项ε的方差为零。
    • D、误差项ε是独立随机变量且服从正态分布，即ε～N（0，σ2）。

    正确答案:A,B,D

  • 第19题：

    单选题
    简单线性回归模型与多元回归模型的基本假设（）
    A

    完全相同

    B

    除了有相同的条件外,后者比前者少

    C

    除了有相同的条件外,后者比前者多

    D

    没有关系


    正确答案： B
    解析： 教材章节/页面：13-304/314

  • 第20题：

    单选题
    除了简单线性回归模型的基本假设条件，多元回归模型还应满足的假设是（）
    A

    误差项u的数学期望值为0

    B

    误差的方差为一常量

    C

    各项误差之间不存在相关关系

    D

    自变量间不存在相关关系


    正确答案： C
    解析： 暂无解析

  • 第21题：

    单选题
    ()是指模型的误差项间存在相关性。
    A

    异方差

    B

    自相关

    C

    伪回归

    D

    多重共线性


    正确答案： A
    解析： 自相关是指模型的误差项间存在相关性。一旦发生自相关，则意味着数据中存在自变量所没有解释的某种形态，说明模型还不够完善。

  • 第22题：

    多选题
    回归模型中，随机误差应该满足的假设条件是（）
    A

    误差的数学期望为0

    B

    误差的方差为0

    C

    误差的数学期望为常量

    D

    误差的方差为常量

    E

    各误差项之间相关关系为正值<br />


    正确答案： A,B
    解析： 暂无解析

  • 第23题：

    判断题
    线性回归分析中，误差项εt均值为0，方差为常数，且不存在自相关，则它是一个白噪声过程。（　　）
    A

    对

    B

    错


    正确答案： 错
    解析：
    若一个随机过程的均值为0，方差为不变的常数，而且序列不存在相关性，这样的随机过程称为白噪声过程。例如，在线性回归分析中的误差项εt服从均值为0，方差为不变常数，即为一个白噪声过程。

相关内容