在区间（0,1)中随机地取两个数，则事件"两数之和小于7/5"的概率为（).（小数作答)

题目

相似考题

1.概率的统计定义是指( )。A．随机现象是可以进行大量的重复试验的B．多次重复试验中事件A发生的频率的大小反映了事件A发生的概率C．两个事件之和的概率等于每个事件概率之和D．两个事件之积的概率等于每个事件概率之积E．两个事件之和的概率等于两个事件概率之积

2.在区间(0, 1)中随机地取两个数, 则两数之差的绝对值小于的概率为____________．

3.五个一位正整数之和为30，其中两个数为1和8，而这五个数和乘积为2520，则其余三个数为（）A．6，6，9B．4，6，9C．5，7，9D．5，8，8

4.古典概率的特征有( )。A．随机现象只有有限个样本点(有限性)B．每个样本点出现的可能性相同(等可能性)C．两个事件之和的概率等于每个事件概率之和D．两个事件之积的概率等于每个事件概率之积E．随机现象有无限个样本点

更多“在区间（0,1)中随机地取两个数，则事件"两数之和小于7/5"的概率为（).（小数作答)”相关问题

第1题：

从3、5、7、11四个数中任取两个数相乘，可以得到多少个不相等的积?
A．5
B．4
C．6
D．7

正确答案：C
[答案] C。解析：四个数两两互质，所以只要选取的乘数不同所得的积就不相同，C₄²=6，选C。
第2题：

● 现实世界中随机性多于确定性。在计算机上模拟随机的实际问题，并进行统计计算，这是非常有用的方法。为此，各种程序设计语言都有产生（伪）随机数的函数。这种函数，每调用一次，就可以获得一个位于区间（0，1）内的数。在程序运行时，多次产生的这些数会均匀地分布在 0、1 之间。在区间（0，1）内均匀分布的含义是指：任取 N 个随机数，当N足够大时，（56）。应用人员可以利用这种随机数来生成满足指定概率分布的数据，并利用这些数据来模拟实际问题。

正确答案：C,A
第3题：

现实世界中随机性多于确定性。在计算机上模拟随机的实际问题，并进行统计计算，这是非常有用的方法。为此，各种程序设计语言都有产生(伪)随机数的函数。这种函数，每调用一次，就可以获得一个位于区间(0，1)内的数。在程序运行时，多次产生的这些数会均匀地分布在0，1之间。在区间(0，1)内均匀分布的含义是指：任取N个随机数，当N足够大时，(56)。应用人员可以利用这种随机数来生成满足指定概率分布的数据，并利用这些数据来模拟实际问题。
某程序每获得一对随机数(x，y)，都判断x2+y2≤1是否成立。如果N对随机数中，有m对满足这个不等式，则当N足够大时，数值m/N将会比较接近(57)。
A．必然有一半数小于1/2，有一半数大于1/2
B．大致顺序、等间隔地排列于(0，1)之间
C．其中落在任意子区间(a，b)中的数的比率大致接近于b-a
D．从小到大排序后，各个数都分别位于(0，1)的Ⅳ等分子区间内

正确答案：C
第4题：

从0到9这10个数中任取一个数并且记下它的值，放回，再取一个数也记下它的值。当两个值的和为8时，出现5的概率是多少？

答案：C
解析：
两个数值的和为8,则可能的情况有0+8、1+7、2+6、3+5、4+4、5+3、6+2、7+1、8+0这9种情况，其中出现5的有2种情况。因此所求概率为2/9
第5题：

从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？

A. 10%
B. 30%
C. 60%
D. 90%

答案：D
解析：
三个数中只要含有1就能满足，共C4,2=6种，三个数中含有2的话，三个数的和必须是偶数，共C3,2-1=2种，不含1和2只有3、4、5能被3整除，因此共有9种满足的情况，总数为c5,3=10，概率为9/10=90%。
第6题：

五个一位正整数之和为30，其中两个数为1和8，而这五个数和乘积为2520，则其余三个数为（）

A. 6，6，9
B. 4，6，9
C. 5，7，9
D. 5，8，8

答案：C
解析：
由结果是2520，个位数是0就可以知道这五个数中含5，2520/5/8=63 ，所以另外两个数为7和9。故答案为C。
第7题：

将3个球随机地放入4个杯子中，则杯中球的最大个数为2的概率为:

答案：C
解析：
提示每次把一个球放入杯中，放入的方法总数n=4X4X4；“最大个数为2”的放入方法总数m=4X(1X3+3X2)。注意第2个球可放在已有1个球的杯中，还有3个空杯子，或放在3个空杯中（有2个杯子各有1个球）。
第8题：

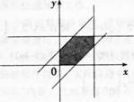
在区间[0，1]中随机抽取两个数(χ，y)，即(χ，y)服从[0，1]上的均匀分布。求这两个数之差的绝对值小于1/2的概率。

答案：
解析：
第9题：

规定：符号“△”为选择两数中较大数，“⊙”为选择两数中较小数。例如：3△5=5，3⊙5=3。那么，[（7⊙3）△5]×[5⊙（3△7）]=（）。
- A、15
- B、21
- C、25
- D、49
正确答案:C
第10题：

在区间（0，1）内随机地取两个数，则所取两数之和不超过5.0概率为（）。

正确答案:1/8
第11题：

从数字1，2，…，10中有放回地任取4个数字，则数字10恰好出现两次的概率为（）

正确答案:0.0486
第12题：

单选题
规定：符号“△”为选择两数中较大数，“⊙”为选择两数中较小数。例如：3△5=5，3⊙5=3。那么，[（7⊙3）△5]×[5⊙（3△7）]=（）。
A
15
B
21
C
25
D
49

正确答案： D
解析：暂无解析
第13题：

从1,3,5,7,9中任取两个数组成一组数，写出其中两数之和小于10的所有数组。

1与3 ，1与5 ，1与7 ，3与5
第14题：

从0、3、5、7、11五个数中任取两个数相乘，可以得到（）个不相等的积。
A．5
B．4
C．6
D．7

正确答案：D
因为0和任何数相乘都等于0，所以其只算是一种乘积，C(2/4)＝6，所以可以得到7个不同的乘积。
第15题：

在所有的1位数中任取一个数,这个数能被2或3整除的概率为________。
A．1/2
B．3/4
C．7/10
D．4/5

正确答案：C
解析：设A={取出的数能被2整除}={0,2,4,6,8},B={取出的数能被3整除}={0,3,6,9},则有A+B={取出的数能被2或3整除}={0,2,3,4,6,8,9},所以P(A+B)=7/10。
第16题：

有68个数排成一排，除头为两个数外，每个数的3倍恰好等于他两边两个数之和。经分析发现，这些数除以6所得的余数以12个数为周期重复出现。已知前两个数是0和1，则该数列最后一个数除以6的余数是（）。

A. 2
B. 3
C. 4
D. 5

答案：D
解析：
解题指导： 68/12=5余8 所以是5个周期后的第八个数 0，1，3，8，21，55，144，377 377/6=62余5，就是5。故答案为D。
第17题：

从3、5、7、11四个数中任取两个数相乘，可以得到多少个不相等的积：
A 5
B 4
C 6
D 7

答案：C
解析：
第18题：

从1到100的整数中任取一个数，则该数能被5或7整除的概率为（）

A.0.02
B.0.14
C.0.2
D.0.32
E.0.34

答案：D
解析：
第19题：

从1、2、3、4、5这五个数字中等可能地、有放回地接连抽取两个数字，则这两个数字不相同的概率为()

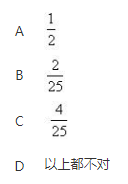答案：D
解析：
第20题：

在区间[0，1]内随机取出两个数，则这两个数的平方和也在区间[0，1]内的概率是（）。
A. 1/2 B.3/4
C.π/4 D.1/4

答案：C
解析：
本题可以借助坐标轴来判断。如右图所示，在第一象限，两个数的平方和在区间[0，1]的条件为：x2+y2≤1( x≥0， y≥0),在区间[0,1]内随机取出两个数，所占面积为边长为1的正方形，两个数的平方和在区间[0，1]所占面积为以1为半径的四分之一圆，因此所求概率为1/4Xπ/1=π/4 。故本题正确答案为C。
第21题：

某随机变量从标准正态分布N（0，1），则此随机变量落入（-1.96，1.96）区间内的概率为（）。
- A、95%
- B、99%
- C、095
- D、0.99
正确答案:A
第22题：

A是任意一个随机事件，则其概率P（A）的取值必然属于（）。
- A、（0，1）
- B、（0，+∞）
- C、（-∞，+∞）
- D、[0，1]
正确答案:D
第23题：

问答题
从0，1，2------9这十个数中不放回随机取4个数能排成4位偶数的概率P1与从中不放回随机取5个数能排成一个5位偶数的概率P2哪个大？

正确答案： P₁=P₂
解析：暂无解析
第24题：

多选题
古典概率的特征有(　　)。
A
随机现象只有有限个样本点
B
每个样本点出现的可能性相同
C
两个事件之和的概率等于每个事件概率之和
D
两个事件之积的概率等于每个事件概率之积
E
无法计算两个事件的概率之和

正确答案： A,B
解析： A是古典概率的有限性，B是等可能性。

在区间（0,1)中随机地取两个数，则事件"两数之和小于7/5"的概率为（).（小数作答)

题目

相似考题

更多“在区间（0,1)中随机地取两个数，则事件"两数之和小于7/5"的概率为（).（小数作答)”相关问题

相关内容