在文本聚类中，欧氏距离是比较适合的。

题目

在文本聚类中，欧氏距离是比较适合的。

相似考题

1.层次聚类适合规模较()的数据集A、大B、中C、小D、所有

2.所谓聚类方法,是采用模式识别中的聚类思想,以类内保持最大相似性以及()保持最大距离为目标,通过迭代优化获得最佳的图像分割阈值。

3.所谓聚类方法,是采用模式识别中的聚类思想,以类内保持最大相似性以及类间保持最 大距离为目标,通过()获得最佳的图像分割阈值。

4.聚类的主要方法不包括()A.划分聚类B.层次聚类C.密度聚类D.距离聚类

参考答案和解析
错误
更多“在文本聚类中，欧氏距离是比较适合的。”相关问题

  • 第1题：

    在k-means或kNN，我们常用欧氏距离来计算最近的邻居之间的距离，有时也用曼哈顿距离，请对比下这两种距离的差别


    正确答案：

    欧氏距离，最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中，如点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的距离为：

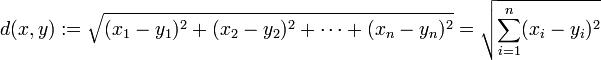
    欧氏距离虽然很有用，但也有明显的缺点。它将样品的不同属性(即各指标或各变量量纲)之间的差别等同看待，这一点有时不能满足实际要求。例如，在教育研究中，经常遇到对人的分析和判别，个体的不同属性对于区分个体有着不同的重要性。因此，欧氏距离适用于向量各分量的度量标准统一的情况。曼哈顿距离，我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离，也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上，坐标(x1, y1)的点P1与坐标(x2, y2)的点P2的曼哈顿距离为：

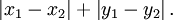
    要注意的是，曼哈顿距离依赖座标系统的转度，而非系统在座标轴上的平移或映射。当坐标轴变动时，点间的距离就会不同。通俗来讲，想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗?显然不是，除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”，这也是曼哈顿距离名称的来源， 同时，曼哈顿距离也称为城市街区距离(City Block distance)。曼哈顿距离和欧式距离一般用途不同，无相互替代性。

  • 第2题：

    欧氏距离测度适用于广播系统中发射点和蜂窝小区中基站位置的选择()


    参考答案：正确

  • 第3题：

    聚类的最简单最基本方法是()。

    A.距离聚类

    B.层次聚类

    C.密度聚类

    D.划分聚类


    正确答案：D

  • 第4题：

    度量距离中,表示各个坐标距离最大值的是()。

    A.欧氏距离

    B.曼哈顿距离

    C.切比雪夫距离


    正确答案:C

  • 第5题：

    若数据量较大，下面哪种方式比较适合（）

    • A、系统聚类
    • B、快速聚类（k-means）
    • C、A和B都可以
    • D、A和B都不可以

    正确答案:B

  • 第6题：

    基于机器学习的系统跟基于人工识别的系统有什么差异？（）

    • A、机器学习系统节省人力，更自动化
    • B、机器学习比较适合排序、简单逻辑判断
    • C、机器学习比较适合复杂的聚类和分类算法
    • D、机器学习可以从海量的数据中获取经验，而不受限于具体维度

    正确答案:A,C,D

  • 第7题：

    开始将N个样品各自作为一类，将规定样品之间的距离和类与类之间的距离，然后将距离最近的两类合并成一个新类，计算新类与其他类的距离，重复进行两个最近类的合并，每次减少一类，直至所有的样品合并为一类，此种聚类方法是（）

    • A、K－means
    • B、SOM聚类
    • C、系统聚类
    • D、有序聚类

    正确答案:C

  • 第8题：

    什么是文本聚类？它和文本分类有何区别于联系？


    正确答案:文本聚类是指利用计算机将文献按其属性相似度聚集成不同的类，生成聚类文件和提供聚类检索。它不同于传统的文献分类。因为它不是基于某种预定的类表，而是基于文献，即先有文献后有类。类的内涵和外延以及整个类体系完全由系统内的文献决定，类的性质时刻与本类文献相一致。
    类的形成过程也不同。传统的文献分类通常按自上而下的顺序一次完成，而聚类则按照自下而上的顺序生成类，且不是一次完成。文献聚类有助于提高检索效率，使属于某一给定类的全部文献在一次文档访问中就可以检出。它可以节省提问处理时间，使检索时不必逐词逐篇的一一比较，只在有关类内部进行比较。

  • 第9题：

    在Word 2003文档中，“段落缩进”是指（）

    • A、两个段落之间的距离
    • B、文本与页眉之间的距离
    • C、文本与页边界之间的距离
    • D、文本与页边距之间的距离

    正确答案:D

  • 第10题：

    问答题
    比较绝对值距离、马氏距离、欧氏距离判别函数之间的异同点。

    正确答案： 1.绝对值距离也叫出租汽车距离或城市块距离。在二维空间中可以看出，这种距离是计算两点之间的直角边距离，相当于城市中出租汽车沿城市街道拐直角前进而不能走两点连接间的最短距离。绝对值距离的特点是各特征参数以等权参与进来，所以也称等混合距离。
    2.欧几里德距离
    欧几里德距离（Euclidean）距离就是两点之间的直线距离（以下简称欧氏距离）。欧氏距离中各特征参数也是等权的。
    绝对值距离和几里德距离都称为闵可夫斯基（Minkowski）距离（以下简称闵氏距离）
    （1）闵氏距离与特征参数的量纲有关。有不同量纲的特征参数的闵氏距离常常是无意义的。
    （2）闵氏距离没有考虑特征参数间的相关性。而哈拉诺比斯距离解决了这个问题。
    3.马哈拉诺比斯距离
    与前两种距离不同，马氏距离是一种加权的欧氏距离，它是通过协方差矩阵来考虑变量相关性的。
    解析： 暂无解析

  • 第11题：

    填空题
    所谓聚类方法，是采用模式识别中的聚类思想，以类内保持最大相似性以及类间保持最 大距离为目标，通过（）获得最佳的图像分割阈值。

    正确答案： 迭代优化
    解析： 暂无解析

  • 第12题：

    单选题
    Ex10_1数据库中是纽约证券交易市场五支股票的星期收益率，共100周的数据。五支股票分别为AlliedChemical，DuPont，UnionCarbide，Exxon，Texaco.为了描述的方便，我们将五支股票分别定义为变量X1，X2，X3，X4，X5，主成分用Yi表示，因子用Fj表示。对五个变量进行聚类，数据经Z分数法标准化，采用最短距离聚类法，欧氏距离平方测度距离，在距离为182.2处可聚为（）
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： D
    解析： 暂无解析

  • 第13题：

    R型聚类统计量有( )。

    A．同号率

    B．绝对距离

    C．欧氏距离

    D．切比雪夫距离


    正确答案：A
    解析：一般来说，R型聚类统计量(或度量)有夹角余弦、相似系数、同号率；Q型聚类统计量(或度量)有：绝对距离、欧氏距离、明考斯基距离、切比雪夫距离、马氏距离、兰氏距离等。选项BCD均属于Q型聚类统计量，故选A。

  • 第14题：

    ()比较适合描述数据在平面或空间中的分布,可以用来帮助分析数据之间的关联,或者观察聚类算法的选择和参数设置对聚类效果的影响。

    A.饼状图

    B.柱状图

    C.折线图

    D.散点图


    正确答案：D

  • 第15题：

    BFR聚类用于在()欧氏空间中对数据进行聚类。

    A.高维

    B.低维

    C.中高维

    D.中维


    正确答案：A

  • 第16题：

    连续型属性的数据样本之间的距离有欧氏距离、曼哈顿距离和（）


    正确答案:明考斯基距离

  • 第17题：

    比较绝对值距离、马氏距离、欧氏距离判别函数之间的异同点。


    正确答案: 1.绝对值距离也叫出租汽车距离或城市块距离。在二维空间中可以看出，这种距离是计算两点之间的直角边距离，相当于城市中出租汽车沿城市街道拐直角前进而不能走两点连接间的最短距离。绝对值距离的特点是各特征参数以等权参与进来，所以也称等混合距离。
    2.欧几里德距离
    欧几里德距离（Euclidean）距离就是两点之间的直线距离（以下简称欧氏距离）。欧氏距离中各特征参数也是等权的。
    绝对值距离和几里德距离都称为闵可夫斯基（Minkowski）距离（以下简称闵氏距离）
    （1）闵氏距离与特征参数的量纲有关。有不同量纲的特征参数的闵氏距离常常是无意义的。
    （2）闵氏距离没有考虑特征参数间的相关性。而哈拉诺比斯距离解决了这个问题。
    3.马哈拉诺比斯距离
    与前两种距离不同，马氏距离是一种加权的欧氏距离，它是通过协方差矩阵来考虑变量相关性的。

  • 第18题：

    以下哪个聚类分析的方法是利用统计学定义的距离进行度量（）

    • A、层次聚类法
    • B、快速聚类法（K-Mans）
    • C、基于密度的聚类法
    • D、基于网格的聚类法

    正确答案:A,B

  • 第19题：

    对样本进行聚类，通常采用的相似性统计量有（）

    • A、绝对距离
    • B、欧氏距离
    • C、夹角余弦
    • D、相关系数
    • E、切比雪夫距离

    正确答案:A,B,E

  • 第20题：

    绝对距离和欧氏距离使用时需要注意哪些问题？


    正确答案: 在使用绝对距离和欧氏距离时，需注意以下两点：
    （1）特征参数的量纲具有不同量纲的特征参数常常是无意义的。例如，特征参数为某个波段亮度值和某种波段亮度比值时，波段的亮度值通常是整数，而比值常为小于1的小数，将这样数量级相差较大的数以同等的权组合起来，只能突出绝对值大的特征参数的作用而降低绝对值小的特征参数的作用。解决的办法是在进行分类前对数据进行标准化。
    （2）特征参数间的相关性特征参数间通常（未经正交变换）是相关的。相关意味着特征参数在表征地物特征方面有共性。若特征参数中的大部分相关性较强，而个别的相关性不大，则一般来说相关的参数和不相关的参数在距离中的权应是不一致的，但在上述公式中权是相同的，这也是个缺点。下面的马氏距离解决了这个问题。

  • 第21题：

    单选题
    若数据量较大，下面哪种方式比较适合（）
    A

    系统聚类

    B

    快速聚类（k-means）

    C

    A和B都可以

    D

    A和B都不可以


    正确答案： A
    解析： 暂无解析

  • 第22题：

    多选题
    对样本进行聚类，通常采用的相似性统计量有（）
    A

    绝对距离

    B

    欧氏距离

    C

    夹角余弦

    D

    相关系数

    E

    切比雪夫距离


    正确答案： C,D
    解析： 暂无解析

  • 第23题：

    填空题
    所谓聚类方法，是采用模式识别中的聚类思想，以（）保持最大相似性以及类 间保持最大距离为目标，通过迭代优化获得最佳的图像分割阈值。

    正确答案： 类内
    解析： 暂无解析

  • 第24题：

    问答题
    绝对距离和欧氏距离使用时需要注意哪些问题？

    正确答案： 在使用绝对距离和欧氏距离时，需注意以下两点：
    （1）特征参数的量纲具有不同量纲的特征参数常常是无意义的。例如，特征参数为某个波段亮度值和某种波段亮度比值时，波段的亮度值通常是整数，而比值常为小于1的小数，将这样数量级相差较大的数以同等的权组合起来，只能突出绝对值大的特征参数的作用而降低绝对值小的特征参数的作用。解决的办法是在进行分类前对数据进行标准化。
    （2）特征参数间的相关性特征参数间通常（未经正交变换）是相关的。相关意味着特征参数在表征地物特征方面有共性。若特征参数中的大部分相关性较强，而个别的相关性不大，则一般来说相关的参数和不相关的参数在距离中的权应是不一致的，但在上述公式中权是相同的，这也是个缺点。下面的马氏距离解决了这个问题。
    解析： 暂无解析

相关内容