用Z变换法求解差分方程时，首先对差分方程作Z变换，然后利用已知初始条件代入Z变换式，求出Y（z)表达式，再对Y（z)求Z反变换，求出差分方程的解。
题目
用Z变换法求解差分方程时，首先对差分方程作Z变换，然后利用已知初始条件代入Z变换式，求出Y（z)表达式，再对Y（z)求Z反变换，求出差分方程的解。
相似考题
更多“用Z变换法求解差分方程时，首先对差分方程作Z变换，然后利用已知初始条件代入Z变换式，求出Y（z)表达式，再对Y（z)求Z反变换，求出差分方程的解。”相关问题
-
第1题：
已知（X,Y）服从均匀分布，联合概率密度函数为
设Z=max｛X,Y｝求Z的概率密度函数fz(z)
答案：X与Y都服从（0, 1）上的均匀分布，则fx与fy在（0, 1）上恒等于1。
Z = z <==> {X = z && Y <= z} + {Y = z && X < z}
因此，fz(z)dz = fx(z)dz * Integrate[fy(z)dy, (0, z)] + fy(z)dz * Integrate[fx(z)dx, (0, z)]
fz(z)dz = zdz + zdz = 2zdz
故fz(z) = 2z，z属于(0, 1). -
第2题：
求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分．答案：解析：
-
第3题：
设随机变量X,Y相互独立,且X～N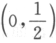
,Y～N
,Z=｜X-Y｜,求
E(Z),D(Z).答案：解析：
-
第4题：
已知x,y,z为自然数,则方程x+y+z=10不同的解有（ ）组A.36
B.66
C.84
D.108
E.120答案：B解析：
-
第5题：
已知直线／：ax+y=1在矩阵
对应的变换作用下变为直线Z：x+by=l
(1)求实数a，b的值；
(2)若点P(x。，yo)在直线Z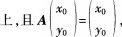
求点P的坐标。 答案：解析：(1）
(2)
-
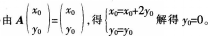
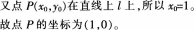
第6题：
设Z=Z(x，Y)是由方程x+y3+z+e2=1确定的函数，求dz答案：解析：利用隐函数求偏导数公式，记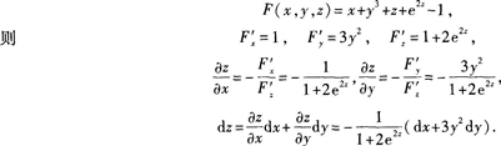
-
第7题：
下列方程是柱面方程的是（）。
- A、x=y=z
- B、y=z2+x
- C、2x+y=0
- D、x+2y+z=1
正确答案:C -
第8题：
用微机实现数字控制算法的基本思想是把D（z）变换为（）
- A、连续方程
- B、离散方程
- C、差分方程
- D、微分方程
正确答案:C -
第9题：
单选题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（ ）。A2
B1
Ce
D0
正确答案： A解析：
构造函数F（x，y，z）＝z－e2x－3z－2y。则∂z/∂x＝－Fx′/Fz′＝2e2x－3z/（1＋3e2x－3z），∂z/∂y＝－Fy′/Fz′＝2/（1＋3e2x－3z），故3∂z/∂x＋（∂z/∂y）＝2。 -
第10题：
单选题曲面xyz=1上平行于x+y+z+3=0的切平面方程是：（）Ax+y+z=0
Bx+y+z=1
Cx+y+z=2
Dx+y+z=3
正确答案： B解析： 暂无解析 -
第11题：
单选题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（ ）。A0
B1
C2
D4
正确答案： B解析：
构造函数F（x，y，z）＝z－e2x－3z－2y。则∂z/∂x＝－Fx′/Fz′＝2e2x－3z/（1＋3e2x－3z），∂z/∂y＝－Fy′/Fz′＝2/（1＋3e2x－3z），故3∂z/∂x＋（∂z/∂y）＝2。 -
第12题：
单选题用微机实现数字控制算法的基本思想是把D（z）变换为（）A连续方程
B离散方程
C差分方程
D微分方程
正确答案： C解析： 暂无解析 -
第13题：
拉氏变换与Z变换公式等类似东西，随便翻翻书把如.h(n)=-a*h(n-1)+b*δ(n) a.求h(
n)的z变换；b.问该系统是否为稳定系统；c.写出FIR数字滤波器的差分方程；（未知）
正确答案：
-
第14题：
设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．答案：解析：
-
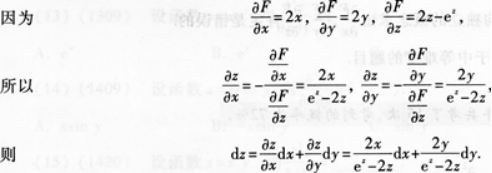
第15题：
若函数z=z(x，y)由方程
确定，则
=_________.答案：1、-dx.解析：
-
第16题：
已知曲面方程为x-yZ+z2-2x+8y+6z=10，则过点(5，-2.1)的切平面方程为( )。A、2x+3y+2z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0答案：B解析：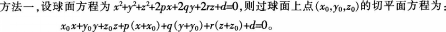
-
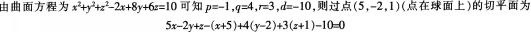
第17题：
已知曲面方程为χ2+y2+z2-2χ+8y+6z=10，则过点(5，-2，1)的切平面方程为( )。A、2χ+y+2z=0
B、2χ+y+2z=10
C、χ-2y+6z=15
D、χ-2y+6z=0答案：B解析：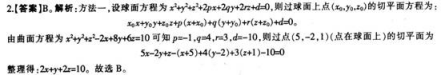
-
第18题：
曲面xyz=1上平行于x+y+z+3=0的切平面方程是：（）
- A、x+y+z=0
- B、x+y+z=1
- C、x+y+z=2
- D、x+y+z=3
正确答案:D -
第19题：
以下（）程序段可以实施X、Y变量值的变换。
- A、Y=X：X=Y
- B、Z=X：Y=Z：X=Y
- C、Z=X：X=Y：Y=Z
- D、Z=X：W=Y：Y=Z：X=Y
正确答案:C -
第20题：
问答题求由方程x2＋y2＋z2－xz－yz－2x－2y＋2z－6＝0确定的函数z＝z（x，y）的极值。正确答案：
先求出函数z的各个偏导:
由原方程可得,原方程两边对x求导得
2x+2z·zx′-z-(x+y)zx′-2+2zx′=0①
原方程两边对y求导得
2y+2z·zy′-z-(x+y)zy′-2+2zy′=0②
①②中,令zx′=0,zy′=0,解得x=(z+2)/2,y=(z+2)/2,将其代入已知方程得Z=±4,故驻点为(3,3)和(-1,-1)。
①式两边对x,y分别求导得
2+2(zx′)2+2zzxx″-2zx′+(2-x-y)zxx″=0③
2zy′zx′+2zzxy″-zy′-zx′+(2-x-y)zxy″=0④
②式两边对y求导得
2+2(zy′)2+2zzyy″-2zy′+(2-x-y)zyy″=0⑤
当x=y=-1,z=-4时,zx′=zy′=0,将其代入③④⑤,得A=zxx″(-1,-1)=1/2,B=zxy″(-1,-1)=0,C=zyy″(-1,-1)=1/2,B2-AC=-1/4<0,A=1/2>0。
则函数z在(-1,-1)处取得极小值z=-4。
当x=y=3,z=4时,zx′=zy′=0,并将其代入③④⑤,得A=zxx″(3,3)=-1/2,B=zxy″(3,3)=0,C=zyy″(3,3)=-1/2,B2-AC=-1/4<0,A=-1/2<0。
故z在(3,3)点处取到极大值z=4。解析： 暂无解析 -
第21题：
填空题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。正确答案： 2解析：
方程两边同时对x求偏导，则∂z/∂x＝e2x－3z（2－3∂z/∂x），可得∂z/∂x＝2e2x－3z/（1＋3e2x－3z）。同理∂z/∂y＝e2x－3z（－3∂z/∂y）＋2，可得∂z/∂y＝2/（1＋3e2x－3z），所以3∂z/∂x＋∂z/∂y＝6e2x－3z/（1＋3e2x－3z）＋2/（1＋3e2x－3z）＝2（1＋3e2x－3z）/（1＋3e2x－3z）＝2。 -
第22题：
单选题设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（ ）。Ax
By
Cz
Dyf（x2－y2）
正确答案： C解析：
由x＋z＝yf（x2－z2），可得∂z/∂x＝－（1－y·2xf′）/（1＋2yzf′），∂z/∂y＝－（－f）/（1＋2yzf′），故有（z∂z/∂x）＋（y∂z/∂y）＝（x－yf＋2xyzf′＋yf）/（1＋2yzf′）＝x。 -
第23题：
单选题利用变量替换u＝x，v＝y/x一定可以把方程x∂z/∂x＋y∂z/∂y＝z化为新方程（ ）。Au∂z/∂u＝z
B∂z/∂v＝z
Cu∂z/∂v＝z
Dv∂z/∂u＝z
正确答案： B解析：
由x∂z/∂x＋y∂z/∂y＝z，得∂z/∂x＝（∂z/∂u）·1＋（∂z/∂v）（－y/x2），∂z/∂y＝（1/x）（∂z/∂v）。
故x∂z/∂x＋y∂z/∂y＝x∂z/∂u－（y/x）（∂z/∂v）＋（y/x）（∂z/∂v）＝x∂z/∂u＝z。
而u＝x，故u∂z/∂u＝z。 -
第24题：
单选题由方程f（y/x，z/x）＝0确定z＝z（x，y）（f可微），则x∂z/∂x＋y∂z/∂y＝（ ）。A－z
Bz
C－y
Dy
正确答案： C解析：
由f（y/x，z/x）＝0可得，∂z/∂x＝－[f1′·（－y/x2）＋f2′·（－z/x2）]/（f2′/x），∂z/∂y＝－（f1′/x）/（f2′/x），则x∂z/∂x＋y∂z/∂y＝－（―yf1′/x―zf2′/x＋yf1′/x）/（f2′/x）＝z。