10、用动态规划方法求背包问题时A．将装载的物品品种数作为阶段数。B．将背包的容量作为决策。C．将背包的容量作为阶段数。D．将装载的物品品种数作为决策。

题目

10、用动态规划方法求背包问题时

A．将装载的物品品种数作为阶段数。

B．将背包的容量作为决策。

C．将背包的容量作为阶段数。

D．将装载的物品品种数作为决策。

相似考题

1.动态规划能解决0／1背包问题的是。()此题为判断题(对，错)。

2.解决0／1背包问题可以使用动态规划、回溯法和分支限界法,其中不需要排序的是动态规划,需要排序的是回溯法,分支限界法。()此题为判断题(对，错)。

3.不能保证求得0-1背包问题的最优解。A．分支限界法B．贪心算法C．回溯法D．动态规划策略

4.解决0／1背包问题只可以使用动态规划和分支限界法。()此题为判断题(对，错)。

更多“10、用动态规划方法求背包问题时”相关问题

  • 第1题：

    动态规划中将所给问题的过程，按（）分解成若干（）的阶段，以便按次序去求每阶段的解。


    参考答案：时间或空间特征；互相联系

  • 第2题：

    *部分背包问题可有贪心法求解：计算Pi/Wi

    数据结构：

    w[i]:第i个背包的重量；

    p[i]:第i个背包的价值；

    1．0-1背包： 每个背包只能使用一次或有限次(可转化为一次)：

    A.求最多可放入的重量。


    正确答案：

     

    NOIP2001 装箱问题
    有一个箱子容量为v(正整数，o≤v≤20000)，同时有n个物品(o≤n≤30)，每个物品有一个体积 (正整数)。要求从 n 个物品中，任取若千个装入箱内，使箱子的剩余空间为最小。
    l 搜索方法
    procedure search(k,v:integer); {搜索第k个物品，剩余空间为v}
    var i,j:integer;
    begin
    if v<best then best:=v;
    if v-(s[n]-s[k-1])>=best then exit; {s[n]为前n个物品的重量和}
    if k<=n then begin
    if v>w[k] then search(k+1,v-w[k]);
    search(k+1,v);
    end;
    end;

    l DP
    F[I,j]为前i个物品中选择若干个放入使其体积正好为j的标志，为布尔型。
    实现:将最优化问题转化为判定性问题
    f [I, j] = f [ i-1, j-w[i] ] (w[I]<=j<=v) 边界：f[0,0]:=true.
    For I:=1 to n do
    For j:=w[I] to v do F[I,j]:=f[I-1,j-w[I]];
    优化：当前状态只与前一阶段状态有关，可降至一维。
    F[0]:=true;
    For I:=1 to n do begin
    F1:=f;
    For j:=w[I] to v do
    If f[j-w[I]] then f1[j]:=true;
    F:=f1;
    End;

  • 第3题：

    利用贪心法求解0/1背包问题时，(26)能够确保获得最优解。用动态规划方求解O/1背包问题时，将“用前i个物品来装容量是x的背包”的0/1背包问题记为KNAP(1，i，X)设fi(X)是KNAP(1，i，X)最优解的效益值，第j个物品的重量和放入背包后取得效益值分别为W和p(j=1～n)，则依次求解f0(X)，f1(X)，…，fn(X)的过程中使用的递推关系式为(27)。

    A．优先选取重量最小的物品

    B．优先选取效益最大的物品

    C．优先选取单位重量效益最大的物品

    D．没有任何准则


    正确答案：C

  • 第4题：

    ● （65） 不能保证求得0-1 背包问题的最优解。

    （65）

    A. 分支限界法

    B. 贪心算法

    C. 回溯法

    D. 动态规划策略


    正确答案：B

  • 第5题：

    0-1背包问题的回溯算法所需的计算时间为（），用动态规划算法所需的计算时间为（）。


    正确答案: O(n*2n)；O(min{nc,2n})

  • 第6题：

    对于0－1背包问题和背包问题的解法，下面（）答案解释正确。

    • A、0－1背包问题和背包问题都可用贪心算法求解
    • B、0－1背包问题可用贪心算法求解，但背包问题则不能用贪心算法求解
    • C、0－1背包问题不能用贪心算法求解，但可以使用动态规划或搜索算法求解，而背包问题则可以用贪心算法求解
    • D、因为0－1背包问题不具有最优子结构性质，所以不能用贪心算法求解

    正确答案:C

  • 第7题：

    动态规划不适用于解决（）。

    • A、排队问题
    • B、背包问题
    • C、资源分配问题
    • D、生产存储问题

    正确答案:A

  • 第8题：

    在用逆向解法求动态规划时，fk（sk）的含义是（）。


    正确答案:从第k个阶段到第n个阶段的最优解

  • 第9题：

    用分枝定界法求极大化的整数规划问题时，任何一个可行解的目标函数值是该问题目标函数值的（）


    正确答案:下界

  • 第10题：

    填空题
    动态规划方法的步骤可以总结为：逆序求解（），顺序求（）、（）和（）。

    正确答案： 最优目标函数,最优策略,最优路线,最优目标函数值
    解析： 暂无解析

  • 第11题：

    单选题
    关于0－1背包问题以下描述正确的是（）
    A

    可以使用贪心算法找到最优解

    B

    能找到多项式时间的有效算法

    C

    使用教材介绍的动态规划方法可求解任意0－1背包问题

    D

    对于同一背包与相同的物品，做背包问题取得的总价值一定大于等于做0－1背包问题


    正确答案： B
    解析： 暂无解析

  • 第12题：

    填空题
    在用逆向解法求动态规划时，fk（sk）的含义是（）。

    正确答案： 从第k个阶段到第n个阶段的最优解
    解析： 暂无解析

  • 第13题：

    用动态规划方法求解0/1背包问题时，将“用前i个物品来装容量是X的背包”的0/1背包问题记为 KNAP(1,i,X)，设fi(X)是KNAP(1,i,X)最优解的效益值，第j个物品的重量和放入背包后取得效益值分别为Wj和巧Pj(j=1～n)。则依次求解f0(X)、f1(X)、…、fn(X)的过程中使用的递推关系式为(58)。

    A．fi(X)=min{fi-1(X),fi-1(X)+pi}

    B．fi(X)=min{fi-1(X),fi-1(X-wi)+pi}

    C．fi(X)=max{fi-1(X),fi-1(X-wi)+pi}

    D．fi(X)=max{fi-1(X-wi),fi-1(X)+pi}


    正确答案：C
    解析：利用贪心法可以解决普通背包问题(即允许将物品的一部分装入背包)，此时使用“优先选取单位重量效益最大的物品”的量度标准可以获得问题最优解，但是贪心法不能用来求解 0/1背包问题。利用动态规划求解0/1背包问题时，按照题目中约定的记号。KNAP(1,i,X)的最优解来自且仅来自于以下两种情况之一：①第i个物品不装入背包，此时最优解的值就是子问题KNAP(1,i-1,X)的最优解的效益值，即为fi-1(X)。②第i个物品装入背包，此时最优解的值为第i个物品的效益值与子问题KNAP(1,i-1,X-Wi)的最优解效益值之和，即为fi-1(X-wi)+pi。由以上分析可知，KNAP(1,i,X)最优解的值为以上两种情况中效益值的更大者，即fi(X)=max{fi-1(X),fi-1(X-wi)+pi}。

  • 第14题：

    利用贪心法求解0/1背包问题时，(55)能够确保获得最优解。用动态规划方法求解 0/1背包问题时，将“用前i个物品来装容量是X的背包”的0/1背包问题记为KNAP(1,i,X)，设fi(x)是KNAP(1,i,X)最优解的效益值，第j个物品的重量和放入背包后取得效益值分别为 wj和pj(j=1～n)。则依次求解f0(x)、f1(x)、...、fn(X)的过程中使用的递推关系式为(56)。.

    A．优先选取重量最小的物品

    B．优先选取效益最大的物品

    C．优先选取单位重量效益最大的物品

    D．没有任何准则


    正确答案：D
    解析：本题考查0/1背包问题的动态规划求解方法。
      利用贪心法可以解决普通背包问题(即允许将物品的一部分装入背包)，此时使用“优先选取单位重量效益最大的物品”的量度标准可以获得问题最优解，但是贪心法不能用来求解0/1背包问题，题目中供选择的A、B、C三种量度标准均不能确保获得最优解。
      利用动态规划求解0/1背包问题时，按照题目中约定的记号。KNAP(1,i,X)的最优解来自且仅来自于以下两种情况之一：
      . 第i个物品不装入背包，此时最优解的值就是子问题KNAP(1,i-1,X)的最优解的效益值，即为fi-1(X)；
      . 第i个物品装入背包，此时最优解的值为第i个物品的效益值与子问题 KNAP(1,i-1,X-wi)的最优解效益值之和，即为fi-1(X-wi)+pi。
      综上，KNAP(1,i,X)最优解的值为以上两种情况中效益值更大者，即取max。

  • 第15题：

    考虑一个背包问题，共有n=5个物品，背包容量为W=10，物品的重量和价值分别为：w={2，2，6，5，4}，v={6,3，5，4，6}，求背包问题的最大装包价值。若此为0-1背包问题，分析该问题具有最优子结构，定义递归式为

    其中c(i，j)表示i个物品、容量为j的0-1背包问题的最大装包价值，最终要求解c(n,W)。 采用自底向上的动态规划方法求解，得到最大装包价值为(62)，算法的时间复杂度为(63)。 若此为部分背包问题，首先采用归并排序算法，根据物品的单位重量价值从大到小排序，然后依次将物品放入背包直至所有物品放入背包中或者背包再无容量，则得到的最大装包价值为(64)，算法的时间复杂度为(65)。

    A.11

    B.14

    C.15

    D.16.67


    正确答案：C

  • 第16题：

    考虑下述背包问题的实例。有5件物品，背包容量为100,每件物品的价值和重量如下表所示，并已经按照物品的单位重量价值从大到小徘好序，根据物品单位重量价值大优先的策略装入背包中，则采用了（请作答此空）设计策略。考虑0/1背包问题（每件物品或者全部放入或者全部不装入背包）和部分背包问题（物品可以部分装入背包），求解该实例，得到的最大价值分别为（ ）。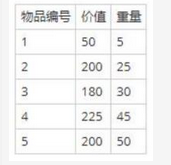

    A.分治
    B.贪心
    C.动态规划
    D.回溯

    答案：B
    解析：
    贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。0/1背包考虑该问题时，只能放入1、2、3号物品，故总价值为430,采用部分背包问题可以将物品拆分，故放1、2、3号物品后还可以放入部分4号物品，故总容量为630。

  • 第17题：

    关于0－1背包问题以下描述正确的是（）

    • A、可以使用贪心算法找到最优解
    • B、能找到多项式时间的有效算法
    • C、使用教材介绍的动态规划方法可求解任意0－1背包问题
    • D、对于同一背包与相同的物品，做背包问题取得的总价值一定大于等于做0－1背包问题

    正确答案:D

  • 第18题：

    解决0/1背包问题可以使用动态规划、回溯法和分支限界法，其中不需要排序的是（），需要排序的是（），（）。


    正确答案:动态规划；回溯法；分支限界法

  • 第19题：

    动态规划方法的步骤可以总结为：逆序求解（），顺序求（）、（）和（）。


    正确答案:最优目标函数；最优策略；最优路线；最优目标函数值

  • 第20题：

    用图解法求线性规划问题时，要求决策变量的个数为（）

    • A、1
    • B、2
    • C、3
    • D、4

    正确答案:B

  • 第21题：

    下列算法中不能解决0/1背包问题的是（）

    • A、贪心法
    • B、动态规划
    • C、回溯法
    • D、分支限界法

    正确答案:A

  • 第22题：

    单选题
    动态规划不适用于解决（）。
    A

    排队问题

    B

    背包问题

    C

    资源分配问题

    D

    生产存储问题


    正确答案： B
    解析： 暂无解析

  • 第23题：

    填空题
    0-1背包问题的回溯算法所需的计算时间为（），用动态规划算法所需的计算时间为（）。

    正确答案： O(n*2n),O(min{nc,2n})
    解析： 暂无解析

  • 第24题：

    单选题
    下列算法中不能解决0/1背包问题的是（）
    A

    贪心法

    B

    动态规划

    C

    回溯法

    D

    分支限界法


    正确答案： A
    解析： 暂无解析

相关内容