某家庭预计在今后10年内的月收入为12000元，如果其中的30%用于支付住房抵押贷款的月还款额，年贷款利率为6%，年存款利率为2%，年通货膨胀率为3%，该家庭有偿还能力的10年期按月等额还款的最大抵押贷款申请额是（）万元。A．32.43 B．37.28 C．39.12 D．40.75

题目

某家庭预计在今后10年内的月收入为12000元，如果其中的30%用于支付住房抵押贷款的月还款额，年贷款利率为6%，年存款利率为2%，年通货膨胀率为3%，该家庭有偿还能力的10年期按月等额还款的最大抵押贷款申请额是（）万元。

A．32.43
B．37.28
C．39.12
D．40.75

相似考题

1.某家庭购买了一套90㎡的商品住宅，售价为4000 元/㎡。该家庭首付了房价总额的30%，其余购房款申请住房公积金和商业组合抵押贷款。住房公积金贷款和商业贷款的利率分别是4．5%和6．8%，贷款期限为15年，按月等额偿还。其中住房公积金贷款的最高限额为10万元。如果该家庭以月收入的35%用来支付抵押贷款月还款额，那么此种贷款方案要求该家庭的最低月收入为多少?假设该家庭在按月还款3年后，于第4年初一次性提前偿还商业贷款本金5万元，那么从第4年起该家庭的抵押贷款的月还款额为多少（8分）

2.某家庭欲购买总价为25万元的一套住宅。该家庭月收入为6000元，准备用月收入的30%来支付抵押贷款月还款额，已知贷款期限为10年，按月等额偿还，年贷款利率为6%。则该家庭的首付款额是（）元。A．34000．00B．83265．38C．87867．78D．91022．12

3.某家庭以住房抵押贷款方式购买了一套住宅，住房抵押贷款期限为20年，年利率为6%，以每月2500元等额还款。该家庭于第9年年初一次性偿还贷款本金10万元，余额在以后的5年内用按月等额还款的方式还清，则最后5年内的月等额还款额为（）元。A．3019.53B．2983.84C．1524.15D．1587.65

4.某家庭预计今后15年内月收入为10000元，如果其中的35%可以用于支付住房抵押贷款的月还款。已知贷款年利率为12%，则该家庭有偿还能力的15年期最大抵押贷款申请额是（）万元。A．28．62B．29．16C．41．56D．48．24

参考答案和解析

答案：A

解析：

等额本息还款方式是在整个贷款期限内以固定月利率和固定月还款额按月偿还贷款本息。月还款额等于以贷款金额为现值计算的年金，计算公式为：

式中，A为月还款额；P为贷款金额；i为贷款月利率；n为按月计算的贷款期限。
根据题意，i＝6%/12，n＝120，A＝12000×30%＝3600，计算得：P＝A/（P/A，i，n）＝32.43。

更多“某家庭预计在今后10年内的月收入为12000元，如果其中的30%用于支付住房抵押贷款的月还款额，年贷款利率为6%，年存款利率为2%，年通货膨胀率为3%，该家庭有偿还能力的10年期按月等额还款的最大抵押贷款申请额是（）万元。”相关问题

第1题：

某家庭欲购买总价为25万元的一套住宅。该家庭月收入为6000元，准备用月收入地30%来支付抵押贷款月还款额。已知贷款期限为10年，按月等额偿还，年贷款利率为6%。则该家庭的首付款额是（）元
A34000.00
B83265.38
C87867.78
D91022.12

正确答案：C
17 月还款额6000×30%=1800元，10年（按月计息为120期），在月利率0.5%（6% ÷12）的现值为P=A[(1+i)n-1]/i
( 1+i)n=1800×[(1+0.5%)120-1/[0.5%( 1+0.5%)120]=162132.22(元)
则该家庭得首付款额是250000-162132.22=87867.78（元）
第2题：

某家庭估计在今后10年内的月收入为16000元，如果月收入的30%可以用于支付住房抵押贷款的月还款，在年贷款利率为12%的情况下，该家庭有偿还能力的最大抵押贷款额是多少？（月收入发生在月初）

正确答案：
337908.13元
第3题：

某家庭向银行申请了总额为30万元、年利率为6％、贷款期限为30年、按月等额还本付息的个人住房抵押贷款。该家庭的月还款额是()元。

A.1798．65
B.2333．33
C.4786．25
D.5018．81

答案：A
解析：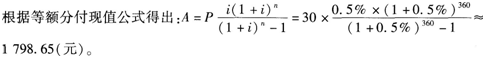
第4题：

某家庭以80万元购买了一套住宅，银行为其提供了15年期的住房抵押贷款，该贷款的年利率为6％，按月等额还款，如果该家庭于第6年初一次提前偿还贷款本金10万元，则从第6年开始的抵押贷款月还款额将减少（　）元。

A、1110.21
B、1244.10
C、1776.32
D、2109.38

答案：A
解析：
本题考查的是复利系数的应用。将第6年初的10万元看作P，在余下的10年中每月等额还款数就是从第6年开始的抵押贷款月还款额减少值。月利率=6%÷12=0.5%，运用公式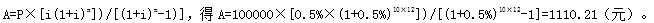
第5题：

银行为某家庭提供年利率为6%，按月等额偿还的10年期个人住房抵押贷款，每月的还款额为7000元，则该家庭在第5年最后一个月的还款额中的利息是（　）元。

A、1836.21
B、1810.39
C、1784.45
D、1795.36

答案：A
解析：
本题考查的是复利计算。根据公式：P=A/i×[1-1/（1+i）^n]，第五年第11个月月末，尚未偿还本金为P=7000/（6%/12）×[1-1/（1+6%/12）^5×12+1]=367242.71（元）。第五年最后一月应还利息I=367242.71×6%/12=1836.21（元）。
第6题：

某家庭欲购买总价为125万元的一套住宅。该家庭月收入为20000元，准备用月收入的40%来支付抵押贷款月还款额。已知贷款期限为10年，按月等额偿还，年贷款利率为6%。则该家庭的首付款额是（　）元。

A.529412.37
B.83265.38
C.87867.78
D.91022.12

答案：A
解析：
本题考查的是复利系数的应用。月还款A＝20000×40%＝8000（元），i＝6%/12＝0.5%，n＝10×12＝120，可负担的贷款额P=A/i×[1-1/(1+i)^n]=8000/0.5%×[1-1/(1+0.5%)^120]=720587.63（元），首付款＝1250000－720587.63＝529412.37（元）。
第7题：

某人准备购买套价格为15万元的住宅，首期付款为25%直接支付，其余申请抵押贷款，期限为8年，利率为15%，按月等额偿还，问月还款额是多少？如果该人40%月收入可用于住房消费，该人月收入应为多少？若抵押贷款宽限两年，（还息不还本，）剩余6年内按月等额偿还，则月还款额是多少？月收入应为多少？

正确答案: （1）贷款数额P=15×（1-25%）=112500元，
i=15%/12=1.25%，
n=12×8=96个月
n=12×6=72个月
（2）月还款额为：
A=P•i•（1+i）n/[（1+i）n-1]=112500*1.25%×（1+1.25%）96/[（1+1.25%）96-1]=2018.86元
该人月收入为2018.86/40%=5047.15元
（3）前两年不偿还本金，也就是P值仍为112500元，要6年偿还，则月还款额为：
A=P•i•（1+i）n，/[（1+i）n，-1]=112500×1.25%×（1+1.25%）72/[（1+1.25%）72-1]=2378.81元
该人月收入为2378.81/40%=5947.04元
第8题：

问答题
某家庭前5年月收入2400元，每月存入银行50%准备购房，现利用该存款本利作为部分购房款，其余房款向银行申请住房抵押贷款，银行要求贷款10年还清，家庭收入现为2400元／月，预计月增0.6%，初步安排月收入的40% 用于还款。问该家庭有偿还能力的住房价格应控制在多少？如市场上房价为2400元／Il12，则所选住房建筑面积应控制在多少？（银行存款利率为6%，贷款利率为9%，其中存款利率为单利，贷款利率为复利，均按月计息）

正确答案：
解析：
第9题：

问答题
计算题：某家庭估计在今后10年内的月收入为20000元，如果其月收入的35%可以用来支付住房抵押贷款的月还款额，在年贷款利率为6%的情况下，该家庭有偿还能力的最大抵押贷款额是多少?

正确答案：该家庭每月用于住房支出的数额A=20000×35%=7000(元)
i=6%/12=0.5%
n=10×12=120(月)
最高贷款额P=A×{,(1+i)n-1,/,i(1+i)n,}
P=7000×{[(1+0.5%)120-1]/[0.5%(1+0.5%)120])=630514.14(元)
解析：暂无解析
第10题：

单选题
某家庭购房抵押贷款10万元，贷款年利率为5%，贷款期限为15年，采用按月等额本金还款方式还，则该家庭第1个月的还款额为（）元。
A
972.56
B
972.22
C
958.35
D
956.35

正确答案： C
解析：暂无解析
第11题：

问答题
某家庭估计在今后10年内的月收入为8000元，如果其月收入的40%可以用来支付住房抵押贷款的月还款额，在年贷款利率为6%的情况下，该家庭有偿还能力的最大抵押贷款额是多少？

正确答案：
解析：
第12题：

问答题
【例5-3】某家庭预计在今后10年内的月收入为16000元，如果其中的30%可用于支付住房抵押贷款的月还款额，年贷款利率为12%，问该家庭有偿还能力的最大抵押贷款申请额是多少？

正确答案：
解析：
第13题：

某家庭以抵押贷款的方式购买了一套价值为30万元的住宅，如果该家庭首付款为房价的20%，其余房款用抵押贷款支付。如果抵押贷款的期限为20年，按月等额偿还，年贷款利率为6%，月还款额为( )元。
A．1655.33
B．1719.43
C．1743.69
D．2149.29

正确答案：B
[答案] B A＝P[i(1+i)n)÷[(1+i)ⁿ-1)
＝300000×80%×[1+0.5%×[(1+0.5%)²⁴⁰]÷[(1+0.5%)²⁴⁰-1)
＝1719.43(元)
第14题：

某家庭向银行申请了总额为30万元、年利率为6％、贷款期限为30年、按月等额还本付息的个人住房抵押贷款。该家庭的月还款额是()元。

A、1798．65
B、2333．33
C、4786．25
D、5018．81

答案：A
解析：
等额本息还款公式计算，A=Pi(1+i)n/[(1+i)n-1]=1798.65元。
第15题：

某家庭预计在今后的10年内的月收入为16000元，如果其中的30%可用于支付住房抵押贷款的月还款额，年利率为12%，问该家庭有偿还能力的最大抵押贷款申请额是多少?

答案：
解析：
该家庭有偿还能力的最大抵押贷款额33.46万元。解 (1)已知该家庭每月可用于支付住房抵押贷款的月还款额：A＝16000×30%＝4800元，月贷款利率为i＝12%/12＝1%，计息周期数：N＝10×12＝120个月。 (2)则该家庭有偿还能力的最大抵押贷款额。
第16题：

某家庭以抵押贷款的方式购买了一套价值为100万元的住宅，首付款为房价的50%，其余房款用抵押贷款支付。如果抵押贷款的期限为20年，按月等额偿还，年贷款利率为12%，问：
（1）抵押贷款额、月贷款利率与月还款额各为多少
（2）如果该家庭30%的收入可以用来支付抵押贷款月还款额，则该家庭须月收入多少，才能购买上述住宅
（3）如果该家庭在按月等额还款5年后，于第6年年初一次提前偿还剩余贷款本息，则还款额为多少

答案：
解析：
（1）抵押贷款额P=100×50%=50万元；
月贷款利率i=12%/12=1%；
月还款额为：A=P×i(1+i)n/[(1+i)n-1]=50×1%(1+1%)240/[(1+1%)240-1]=0.550543万元=5505.43元；
（2）该家庭欲购买上述住宅，其月收入须为：5505.43/30%=18351.43元
（3）该家庭在第6年年初一次提前偿还剩余贷款余额时，所需偿还金额为
Pn=A[（（1+i）n-m-1）/[i（1+i）n-m]，其中，n=12×20=240，m=12×5=60，
代入数据，得到Pn=5505.43×[（（1+1%）240-60-1）/[1%（1+1%）240-60]=458721.59元=45.87万元。
第17题：

某家庭欲购买总价为125万元的一套住宅。该家庭月收入为20000元，准备用月收入的40%来支付抵押贷款月还款额。已知贷款期限为10年，按月等额偿还，年贷款利率为6%。则该家庭的首付款额是（　）元。

A、529412.37
B、83265.38
C、87867.78
D、91022.12

答案：A
解析：
本题考查的是复利系数的应用。月还款A＝20000×40%＝8000（元），i＝6%/12＝0.5%，n＝10×12＝120，可负担的贷款额P=A/i×[1-1/(1+i)n]=8000/0.5%×[1-1/(1+0.5%)120]=720587.63（元），首付款＝1250000－720587.63＝529412.37（元）。
第18题：

某家庭预计今后20年内的每月月末收入为6800元，如月收入的40%可以用于支付住房抵押贷款的月还款额，在年贷款利率为6%的情况下，该家庭有偿还能力的最大抵押贷款额为（）万元。
A. 37.97 B. 37.44 C. 94.93 D. 37.87

答案：A
解析：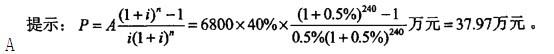
第19题：

计算题:某家庭购买了一套90m2的商品住宅，售价为4000元/m2。该家庭首付了房价总额的30%，其余购房款申请住房公积金和商业组合抵押贷款。住房公积金贷款和商业贷款的利率分别是4.5%和6.8%，贷款期限为15年，按月等额偿还。其中住房公积金贷款的最高限额为10万元。如果该家庭以月收入的35%用来支付抵押贷款月还款额，那么此种贷款方案要求该家庭的最低月收入为多少?假设该家庭在按月还款3年后，于第4年初一次性提前偿还商业贷款本金5万元，那么从第4年起该家庭的抵押贷款的月还款额为多少?

正确答案: (一)解法一：
(1)已知P=4000×90×(1-30%)=25.2万元
P1=10万元;P2=(25.2-10)=15.2万元
(2)N=15×12=180月
=4.5%/12=0.375%i2=6.8%/12=0.57%(0.567%，0.5667%)
A1=P1×[i1×(1-i1)n]/[(1+i1)n-1]=10000×[0.375%×(1+0.375%)180]/[(1+0.375%)180-1]
=764.99元
Al=P2×[i2×(1-i2)n]/[(1+i2)n-1]=15200×[0.57%×(1+0.57%)180]/[(1+0.57%)180-1]
=1352.66元(按照0.57%)
=1349.62元(按照0.567%)
=1349.31元(按照0.5667%)
A=A1+A2=764.99+1352.66=2117.65元(按照0.57%)
=2114.61元(按照0.567%)
=2114.3元(按照0.5667%)
(3)最低月收入=A/0.35=2117.65/0.35=6050.43元(按照O.57%)
=6041.74元(按照0.567%)
=6040.86元(按照0.5667%)
(4)第4年初一次偿还商贷本金5万元，在第4年第15年内的月还款额为：
P1=5万元n=(15-3)×12=144月
A’=P×P2×[i2(1+i2)n]/[(1+i2)n-1]
=5×[O.57%×(1+O.57)n]/[(1+O.57%)n-1]
=509.94元(按照O.57%)
=508.98元(按照0.567%)
=508.89元(按照0.5667%)
从第4年起抵押贷款月还款额为：A-A’=2117.65-509.94=1607.71元(按照O.57%)
(二)解法二：
(1)～(3)与解法一相同
(4)还款3年后，尚未偿还商业贷款n=(15-3)×12=144月
(5)第4年初还款5万元后，商业贷款月还款额A：
P3=132630.40-50000=82630.4元
A3=82630.4[O.57%×(1+O.57%)144]/[(1+O.57%)144-1]=842.72
(6)该家庭第4年初的月还款额为：
A1+A2=764.99+842.72=1607.71元
第20题：

问答题
某人准备购买套价格为15万元的住宅，首期付款为25%直接支付，其余申请抵押贷款，期限为8年，利率为15%，按月等额偿还，问月还款额是多少？如果该人40%月收入可用于住房消费，该人月收入应为多少？若抵押贷款宽限两年，（还息不还本，）剩余6年内按月等额偿还，则月还款额是多少？月收入应为多少？

正确答案：（1）贷款数额P=15×（1-25%）=112500元，
i=15%/12=1.25%，
n=12×8=96个月
n=12×6=72个月
（2）月还款额为：
A=P•i•（1+i）n/[（1+i）n-1]=112500*1.25%×（1+1.25%）96/[（1+1.25%）96-1]=2018.86元
该人月收入为2018.86/40%=5047.15元
（3）前两年不偿还本金，也就是P值仍为112500元，要6年偿还，则月还款额为：
A=P•i•（1+i）n，/[（1+i）n，-1]=112500×1.25%×（1+1.25%）72/[（1+1.25%）72-1]=2378.81元
该人月收入为2378.81/40%=5947.04元
解析：暂无解析
第21题：

问答题
某家庭估计在今后10年内的月收入为16000元,如果月收入的30%可以用于支付住房抵押贷款的月还款,在年贷款利率为12%的情况下, 该家庭有偿还能力的最大抵押贷款额是多少?(月收入发生在月初)

正确答案： 337908.13元
解析：暂无解析
第22题：

单选题
某家庭预计今后15年内月收入为12000元，如果其中的35％可以用于支付住房抵押贷款的月还款。已知贷款年利率为12％，则该家庭有偿还能力的15年期最大抵押贷款申请额是（）万元。
A
28.62
B
29.16
C
35.00
D
48.24

正确答案： A
解析：
第23题：

单选题
某家庭预计今后20年内的每月月末收入为6800元，如月收入的40%可以用于支付住房抵押贷款的月还款额，在年贷款利率为6%的情况下，该家庭有偿还能力的最大抵押贷款额为（）万元。
A
37.97
B
37.44
C
94.93
D
37.87

正确答案： D
解析：暂无解析

题目

相似考题

参考答案和解析

相关内容