设n阶矩阵A有一个特征值3，则|-3E+A|=_________.

题目

设n阶矩阵A有一个特征值3，则|-3E+A|=_________.

相似考题

1.设A是n阶实对称矩阵，则A有n个()特征值.

2.设n阶矩阵A与对角矩阵相似,则().A.A的n个特征值都是单值 B.A是可逆矩阵 C.A存在n个线性无关的特征向量 D.A一定为n阶实对称矩阵

3.设A是n阶矩阵，且Ak=O(k为正整数)，则( )。A.A一定是零矩阵 B.A有不为0的特征值 C.A的特征值全为0 D.A有n个线性无关的特征向量

4.设A是n阶矩阵,且E＋3A不可逆,则()。A.3是A的特征值B.-3是A的特征值C.1/3是A的特征值D.-1/3是A的特征值

更多“设n阶矩阵A有一个特征值3,则|－3E＋A|=_________. ”相关问题

  • 第1题：

    设A是三阶矩阵，有特征值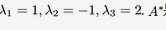是A的伴随矩阵，E是三阶单位阵，则


    答案：
    解析：

  • 第2题：

    设A是3阶矩阵，有特征值1，-2，4，则2E-A是满秩的。（）


    正确

  • 第3题：

    设A为n阶矩阵，若方程AX=0有非零解，则A必有一个特征值为（)


    0

  • 第4题：

    设矩阵A为n阶实矩阵，n为奇数，则下列叙述正确的是________

    A．矩阵A一定有实特征值

    B．矩阵A可能有复特征值

    C．矩阵A有n个线性无关的特征向量

    D．矩阵A线性无关的特征向量个数可能少于n


    设Ap (i) =λ i p (i) i=12…n．已知当i≠j时p (i)T p (j) =0．因此 p (i)T Ap (j) =λ j p (i)T p (j) =0 i≠j．故p (1) p (2) …p (n) 关于A共轭． 设Ap(i)=λip(i),i=1,2,…,n．已知当i≠j时,p(i)Tp(j)=0．因此p(i)TAp(j)=λjp(i)Tp(j)=0,i≠j．故p(1),p(2),…,p(n)关于A共轭．

  • 第5题：

    设n阶矩阵A，B有相同的特征值，则A，B一定相似。


    证 证法1 若0为AB的特征值，则|AB|=0，从而有|BA|=|B||A|=|A||B|=|AB|=0，因此，0也是BA的特征值. 若λ 0 为AB的非零特征值，则有x≠0，使ABx=λ 0 x，由此可知Bx≠0，用B左乘ABx=λ 0 x的两端，得 (BA)(Bx)=λ 0 (Bx) 由于列向量Bx≠0，故λ 0 是BA的一个特征值且Bx为对应的一个特征向量. 所以，AB的特征值都是BA的特征值，同理可证BA的特征值也都是AB的特征值.因此，AB与BA有相同的特征值. 证法2 可见AB与BA的属于同一特征值的特征向量是不同的.

相关内容