31、给定带权无向图,用普里姆和克鲁斯卡尔算法得到的最小代价生成树的代价相同
题目
31、给定带权无向图,用普里姆和克鲁斯卡尔算法得到的最小代价生成树的代价相同
相似考题
更多“31、给定带权无向图,用普里姆和克鲁斯卡尔算法得到的最小代价生成树的代价相同”相关问题
-
第1题:
常用的最小生成树算法有()A、普里姆算法
B、克鲁斯卡尔算法
C、哈夫曼算法
D、拓扑算法
参考答案:AB
-
第2题:
对于含n个顶点、e条边的无向连通图,利用Prim算法构造最小生成树的时间复杂度(),用Kruskal算法构造最小生成树的时间复杂度为()。A.O(n)
B.O(n²)
C.O(e)
D.O(eloge)
F.O(e²)
参考答案:B,D
-
第3题:
带权无向图的最小生成树是唯一的。
此题为判断题(对,错)。
正确答案:×
-
第4题:
已知一个图的顶点集V和边集E分别为:
V={1,2,3,4,5,6,7};
E={(1,2)3,(1,3)5,(1,4)8,(2,5)10,(2,3)6,(3,4)15,(3,5)12,(3,6)9,(4,6)4,(4,7)20,(5,6)18,(6,7)25};
按照普里姆算法从顶点1出发得到最小生成树,试写出在最小生成树中依次得到的各条边。
正确答案:普里姆算法从顶点1出发得到最小生成树为:
(1,2)3, (1,3)5, (1,4)8, (4,6)4, (2,5)10, (4,7)20
-
第5题:
如下所示是一个带权连通无向图,其最小生成树各边权的总和为
A.24
B.25
C.26
D.27
正确答案:C
-
第6题:
在求边稠密的图的最小代价生成树时,()算法比较合适。A.普里姆(Prim)
B.克鲁斯卡尔(Kruskal)
C.迪杰斯特拉(Dijkstra)
D.其他答案:A解析:
-
第7题:
对于一个带权连通图,在什么情况下,利用普里姆(Prim)算法与利用克鲁斯卡尔(Kruskal)算法可能生成不同的最小生成树?
正确答案:当图中出现权值相同的边时,利用普里姆(Prim)算法与利用克鲁斯卡尔(Kruskal)算法可能生成不同的最小生成树。 -
第8题:
带权连通图的最小生成树的权值之和一定小于它的其它生成树的权值之和。
正确答案:正确 -
第9题:
一个带权无向图的最小生成树是否一定唯一?在什么情况下构造出的最小生成树可能不唯一?
正确答案: 一个带权无向图的最小生成树不一定是唯一的。从Kruskal算法构造最小生成树的过程可以看出,当从图中选择当前权值最小的边时,如果存在多条这样的边,并且这些边与已经选取的边构成回路,此时这些边就不可能同时出现在一棵最小生成树中,对这些边的不同选择结果可能会产生不同的最小生成树。 -
第10题:
任何带权的无向图都存在最小(代价)生成树。
正确答案:错误 -
第11题:
判断题任何带权的无向图都存在最小(代价)生成树。A对
B错
正确答案: 对解析: 暂无解析 -
第12题:
问答题对于一个带权连通图,在什么情况下,利用普里姆(Prim)算法与利用克鲁斯卡尔(Kruskal)算法可能生成不同的最小生成树?正确答案: 当图中出现权值相同的边时,利用普里姆(Prim)算法与利用克鲁斯卡尔(Kruskal)算法可能生成不同的最小生成树。解析: 暂无解析 -
第13题:
对(),用Prim算法求最小生成树较为合适,而Kruskal算法适于构造()图的最小生成树。A.完全图
B.连通图
C.稀疏图
D.稠密图
参考答案:D,C
-
第14题:
如图所示的带权无向图的最小生成树的权为 ( )
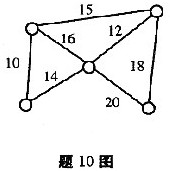
A.51
B.52
C.54
D.56
正确答案:C
解析:根据最小生成树的构造过程,可知在构造本题中无向图的最少生成树时,将选取权值分别为10、14、12、18的边,所以此最小生成树的权即各边权值之和即54。 -
第15题:
Prim算法和Kruscal算法都是无向连通网的最小生成树的算法,Prim算法从一 个顶点开始,每次从剩余的顶点加入一个顶点,该顶点与当前生成树中的顶占的连边权重 最小,直到得到最小生成树开始,Kruscal算法从权重最小的边开始,每次从不在当前的生成树顶点之间的边中选择权重最小的边加入,直到得到一颗最小生成树,这两个算法都采用了( )设计策略,且( )。
A.分治 B.贪心 C.动态规划 D.回溯 A.若网较稠密,则Prim算法更好 B.两个算法得到的最小生成树是一样的 C.Prim算法比Kruscal算法效率更高 D.Kruscal算法比Prim算法效率更高
正确答案:B,A
-
第16题:
下面有关图的相关概念说法不正确的是【】
A.有e条边的无向图,在邻接表中有e个结点
B.有向图的邻接矩阵是对称的
C.任何无向图都存在生成树
D.不同的求最小生成树的方法最后得到的生成树的权值之和是相等的
正确答案:ABC
-
第17题:
Prim算法和Kruscal算法都是无向连通网的最小生成树的算法,Prim算法从一个顶点开始,每次从剩余的顶点中加入一个顶点,该顶点与当前的生成树中的顶点的连边权重最小,直到得到一颗最小生成树;Kruscal算法从权重最小的边开始,每次从不在当前的生成树顶点中选择权重最小的边加入,直到得到一颗最小生成树,这两个算法都采用了 (请作答此空) 设计策略,且 ( ) 。A.分治
B.贪心
C.动态规划
D.回溯答案:B解析:Prim算法从扩展顶点开始,每次总是"贪心的"选择与当前顶点集合中距离最短的顶点,而Kruscal 算法从扩展边开始,每次总是"贪心的"选择剩余的边中最小权重的边,因此两个算法都是基于贪心策略进行的。
Prim 算法的时间复杂度为O(n2),其中n 为图的顶点数,该算法的计算时间与图中的边数无关,因此该算法适合于求边稠密的图的最小生成树;Kruscal 算法的时间复杂度为O(mlgm) ,其中m 为图的边数,该算法的计算时间与图中的顶点数无关,因此该算法适合于求边稀疏的图的最小生成树。当图稠密时,用 Prim 算法效率更高。但若事先没有关于图的拓扑特征信息时,无法判断两者的优劣。由于一个图的最小生成树可能有多棵, 因此不能保证用这两种算法得到的是同一棵最小生成树。 -
第18题:
Prim算法和Kruscal算法都是无向连通网的最小生成树的算法,Prim算法从一个顶点开始,每次从剩余的顶点中加入一个顶点,该顶点与当前的生成树中的顶点的连边权重最小,直到得到一颗最小生成树;Kruscal算法从权重最小的边开始,每次从不在当前的生成树顶点中选择权重最小的边加入,直到得到一颗最小生成树,这两个算法都采用了(64)设计策略,且(65)。A.分治
B.贪心
C.动态规划
D.回溯答案:B解析:Prim算法和Kruscal算法都是基于贪心算法的应用。Prim算法的时间复杂度为O(n2),与图中边数无关,该算法适合于稠密图。Kruskal算法的时间复杂度只和边有关系,为O(elog2e),由于Kruskal算法只与边有关,因此适合求稀疏图的最小生成树。 -
第19题:
n个顶点的带权无向连通图的最小生成树包含()个顶点。
- A、n-1
- B、n
- C、n/2
- D、n+1
正确答案:B -
第20题:
采用不同的遍历方法,所得到的无向图的生成树总是相同的。
正确答案:错误 -
第21题:
对于含有N个顶点E条边的无向连通图,利用Kruskal算法生成最小代价生成树的时间复杂度为()。
正确答案:o(elg0) -
第22题:
填空题对于含有N个顶点E条边的无向连通图,利用Kruskal算法生成最小代价生成树的时间复杂度为()。正确答案: o(elg0)解析: 暂无解析 -
第23题:
问答题一个带权无向图的最小生成树是否一定唯一?在什么情况下构造出的最小生成树可能不唯一?正确答案: 一个带权无向图的最小生成树不一定是唯一的。从Kruskal算法构造最小生成树的过程可以看出,当从图中选择当前权值最小的边时,如果存在多条这样的边,并且这些边与已经选取的边构成回路,此时这些边就不可能同时出现在一棵最小生成树中,对这些边的不同选择结果可能会产生不同的最小生成树。解析: 暂无解析 -
第24题:
单选题n个顶点的带权无向连通图的最小生成树包含()个顶点。An-1
Bn
Cn/2
Dn+1
正确答案: C解析: 暂无解析
