12件产品中有4件次品，在先取一件的情况下，任取两件产品皆为正品，则先取一件为次品的概率为（）

第1题：

第2题：

正确答案：

第3题：

第4题：

在一批N个产品中有M个次品，从这批产品中任取n个产品，其中含有m个次品的概率是( )。

第5题：

答案：

解析：

第6题：

答案：

解析：

第7题：

答案：

解析：

(1)令Ai={第i次取到正品}（i=1，2），则

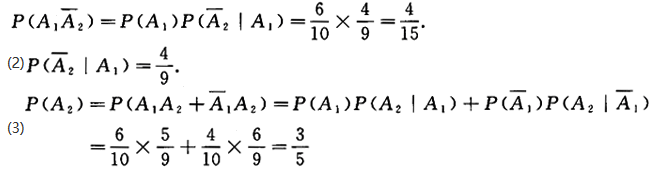
第8题：

答案：

解析：

第9题：

答案：

解析：

令A={第一件产品合格），B={第二件产品合格），则所求概率为　　

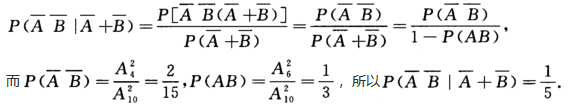
第10题：

答案：

解析：

第11题：

设工厂A和工厂B的产品的次品率分别为1%和2%，现从由A和B的产品分别占60%和40%的一批产品中随机抽取一件，发现是次品，则该次品属于A生产的概率是（）.

第12题：

设有一仓库有一批产品，已知其中50%、30%、20%依次是甲、乙、丙厂生产的，且甲、乙、丙厂生产的次品率分别为1/10，1/15，1/20，现从这批产品中任取一件，求取得正品的概率（）

• A、0.62
• B、0.72
• C、0.82
• D、0.92

第13题：

第14题：

第15题：

正确答案：B

第16题：

答案：

解析：

由题意，x的所有可能的取值为1，2，3，

第17题：

答案：

解析：

第18题：

答案：D

解析：

设B={从乙箱中取得正品}，A1={从甲箱中取出3个正品}，A2={从甲箱中取出2个正品1个次品}，A3={从甲箱中取出1个正品2个次品}，A4 ={从甲箱中取出3 个次品}，显然A1、A2、A3、A4都是互斥的，所以B=B(A1 + A2+ A3+ A4)。


P(B A1) =7/10，P(B A2) =6/10，P(B A3) =5/10，P(B A4) =4/10；
故P(B) =P(BA1+BA2 + BA3+ BA4) =P(A1)P(B A1) +P(A2)P(B A2) +P(A3)P (B A3) +P(A4)P(B A4) = (10/56) x (7/10) + (30/56) x (6/10) + (15/56) x (5/ 10) + (1/56) x (4/10) =0.5875。

第19题：

答案：

解析：

第20题：

答案：

解析：

【解】设Ai={第i次取到次品}(i=1，2，3).
(1)
(2)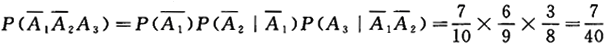（试验还没有开始，计算前两次都取不到次品，且第三次取到次品的概率）.
(3)（已知前两次已发生的结果，唯一不确定的就是第三次）.
(4)

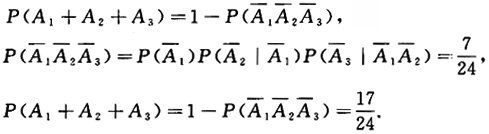
第21题：

10件产品中有4件不合格，从中任取两件，已知取出的两件中有一件不合格，则另一件也是不合格品的概率是（ ）。

答案：D

解析：

第22题：

设10件产品有4件不合格品，从中任取两件，已知所取两件产品中有一件是不合格品，则另一件也是不合格品的概率是（）.

第23题：

某工厂的次品率为5%，并且正品中有80%为一等品，如果从该厂的产品中任取一件来检验，那么检验结果是一等品的概率为19/25

第24题：