以下程序解决猴子吃桃问题。问题描述:猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想再吃时,就只剩一个桃子了。求第1天共摘多少个桃子。 #include <stdio.h> void main(){ int d,s=1; for(d=10;d>1; _____) { ___________ ; } printf("第一天的桃子数:%dn",s); }A.d++ ,s=(s-1)*2B.
题目
以下程序解决猴子吃桃问题。问题描述:猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想再吃时,就只剩一个桃子了。求第1天共摘多少个桃子。 #include <stdio.h> void main(){ int d,s=1; for(d=10;d>1; _____) { ___________ ; } printf("第一天的桃子数:%dn",s); }
A.d++ ,s=(s-1)*2
B.d-- , s=(s+1)*2
C.d-- ,s=s*2
D.d+2 ,s=(s-1)*2
相似考题
更多“以下程序解决猴子吃桃问题。问题描述:猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想再吃时,就只剩一个桃子了。求第1天共摘多少个桃子。 #include <stdio.h> void main(){ int d,s=1; for(d=10;d>1; _____) { ___________ ; } printf("第一天的桃子数:%dn",s); }”相关问题
-
第1题:
从前有一个人,因饥饿一连买了6个饼子吃,但是还不觉得饱,于是就买了第7个。刚吃了一半就饱了。那人很后悔,说:“前6个饼子都白吃了,如果早知道这半个饼子就能吃饱,我只吃这半个饼子就行了。”从哲学角度看,这个吃饼人错在( )。
A.不懂得量变是质变的必要准备
B.否认了事物的质变
C.看不到量的积累的重要性
D.割裂事物的联系,孤立地看问题
正确答案:ACD
量变是质变的必要准备,质变是量变的必然结果。题干看到了质变,而没有看到量变,割裂了事物之间的联系。因此B项错误。 -
第2题:
审美是一种实用而又使人产生情感愉悦的活动,和猴子吃桃子无异。()此题为判断题(对,错)。
正确答案:×
-
第3题:
阅读以下函数说明和C语言函数,将应填入(n)处的语句写在对应栏内。
【函数2.1说明】
将一个正整数分解质因数。例如:输入90,打印出90=2*3*3*5。
【函数2.1】
Fun1 (int n)
{
int i;
for(i=2;i<=n;i++)
{
while ((1))
{
if (n%i==0)
{
printf("%d*",i);
(2);
}
else
break;
}
}
printf("%d",\n);
}
【函数2.2说明】
下面程序的功能是:海滩上有一堆桃子,5只猴子来分。第1只猴子把这堆桃子平均分为5份,多了一个,这只猴子把多的一个扔入海中,拿走了一份。第2只猴子把剩下的桃子又平均分成5份,又多了一个,它同样把多的一个扔入海中,拿走了一份。第 3、4、5只猴子都是这样做的,问海滩上原来最少有多少个猴子?
【函数2.2】
main()
{
int i,m,j,k,count;
for(i=4;i<10000;i+=4)
{
count=0;
(3);
for(k=0;k<5;k++)
{
(4);
i=j;
if(j%4==0)
(5);
else
break;
}
i=m;
if(count==4)
{
printf("%d\n",count);
break;
}
}
}
正确答案:(1)n!=i (2)n=n/i (3)m=i (4)j=i/4*5+1 (5)count++
(1)n!=i (2)n=n/i (3)m=i (4)j=i/4*5+1 (5)count++ 解析:本题考查C语言中正整数分解质因数算法和猴子分桃算法的实现。
在程序2.1中,要求将一个正整数分解质因数。我们先来了解一下质因数的概念,一个自然数的因数中,为质数的因数叫做这个数的质因数。把一个合数,用质因数相乘的形式表示出来,叫做分解质因数。如90=2*3*3*5,其中2,3,5都是质数。在对数n进行分解质因数时,应先找到一个最小的质数i,然后按下述步骤完成:
(1)判断这个质数i是否等于n,如果相等,则说明分解质因数的过程已经结束,打印出结果即可。
(2)如果n≠i,但n能被i整除,则i是n的质因数,应打印出i的值,并用n除以 i的商,作为新的正整数n。
(3)如果n不能被i整除,则用i+1作为i的值,重复执行第(1)步。
通过代码我们已经知道了最小的质数为2,第(1)空是循环的判断条件,结合我们上面的分析,应该是判断质数i是否等于n,因此,此空答案为n!=i。
第(2)空在条件判断语句下,条件n%i==0成立,说明n能被i整除,根据分析,应打印出i的值,并用n除以i的商,作为新的正整数n。代码中已经实现了对i的输出,第(2)空的任务是用n除以i的商,作为新的正整数n,因此,答案为n=n/i。
在程序2.2中,要求我们求出原来海滩上的桃子数,这个数的特点是除以5余1,且减去它的商和余数后再除以5又余1,一直这样下去,直到最后一次。要求这样一个有特点的数,我们可以在一个较大的范围里编程去找具有这种性质的数。结合代码我们知道,程序设计是从4到10000这个范围里去找具有这种特征的数的基数。
第(3)空所在位置是第一层循环下面,应该是给变量赋初值阶段,结合后面的程序,可以发现m是用来临时存放当前求的基数乙因此,此空答案为m=i。
第(4)空在第二层循环下面,这个循环的作用是利用当前的基数i来求桃子数,那么求解的过程肯定是分桃过程的逆向过程。即此空的答案为i=i/4*5+1。
第(5)空在条件判断语句下面,如果条件成立,则执行此语句。我们接着看下面的程序,发现程序中有语句if(count==4),而在程序中一直没有出现变量count的值改变的语句,而它的初值是0,因此,此空肯定用来改变count的值的,再结合猴子分桃的特性,可以得到此空的答案为count++。 -
第4题:
山顶上有棵橘子树,一只猴子吃橘子,第一天吃了全部的十分之一,第二天吃了当天树上的九分之一第九天吃了当天树上的二分之一,第十天将树上剩下的10个橘子全部吃完.问:树上原有多少个橘子?()
A.100
B.120
C.150
D.200
正确答案:A
A[解析]本题采用倒推法,从第十天向前推算,由已知条件,这10个橘子是第九天的1/2,所以第九天的橘子为10÷1/2=20(个);这20个橘子又是第八天的2/3,所以第八天的橘子为20÷2/3=30(个);如此继续下去,就可知树上原有橘子为:10÷(1-1/9)÷(1-1/3)÷…÷(1-1/9)÷(1-1/10)=100(个).故本题正确答案为A. -
第5题:
—只猴子摘了一堆桃子,第一天它吃了这堆桃子的七分之一,第二天它吃了余下桃子的六分之一,第三天它吃了余下桃子的五分之一,第四天它吃了余下桃子的四分之一,第五天它吃了余下桃子的三分之一,第六天它吃了余下桃子的二分之一,这时还剩12只桃子,那么第一天和第二天所吃桃子的总数是多少只?( )
A. 10 B. 12 C. 18 D. 24答案:D解析:此类题用倒推法来解比较适宜,即从最后12只桃子开始,逐步倒推。
最后桃子数:12只。
所以第一天和第二猴子吃桃子总数是:(84-72)+(72-60)=24(只)。 -
第6题:
某单位行政采购了一批水果作为员工的下午茶,共有若干箱苹果和桃子,苹果的箱数是桃 子箱数的 4 倍,如果每天吃 2 箱桃子和 6 箱苹果,那么桃子吃完时还剩 15 箱苹果。 该单位采购了( )箱桃子。A.15
B.20
C.30
D.60答案:A解析:因为苹果箱数是桃子的4倍,如果每天吃2箱桃子和8箱苹果,桃子和苹果可以同时吃完。现在每天少吃8-6=2箱苹果,还剩15箱苹果,因此吃了15÷2=7.5天,故桃子有2×7.5=15箱。 -
第7题:
勃艮第红葡萄酒的典型水果特征是()。
- A、热带水果
- B、草莓
- C、黑加仑
- D、桃子
正确答案:B -
第8题:
()张无忌过了狭缝,逃脱了朱长龄之手,来到了别有洞天,首先吃了个什么水果?
- A、桃子
- B、苹果
- C、梨子
- D、以上均错
正确答案:D -
第9题:
在一堆桃子旁边住着5只猴子。深夜,第一只猴子起来偷吃了一个,剩下的正好平均分成5份,它藏起自己的一份,然后去睡觉。过了一会儿,第二只猴子起来也偷吃了一个,剩下的也正好平均分成5份,它也藏起自己的一份,然后去睡觉。第三、四、五只猴子也都依次这样做。问那堆桃子最少有多少个()
- A、4520
- B、3842
- C、3121
- D、2101
正确答案:C -
第10题:
单选题某单位行政采购了一批水果作为员工的下午茶,共有若干箱苹果和桃子,苹果的箱数是桃子箱数的4倍,如果每天吃2箱桃子和6箱苹果,那么桃子吃完时还剩15箱苹果。该单位采购了( )箱桃子。A15
B20
C30
D60
正确答案: A解析: -
第11题:
单选题猴子第1天摘下若干个桃子,当即吃了一半又一个。第2天又把剩下的桃吃了一半有一个,以后每天都吃前一天剩下的桃子的一半又一个,到第5天猴子想吃的时候,只剩下一个桃子。问猴子第1天一共摘了多少桃子?()。A46
B44
C22
D10
正确答案: D解析: 暂无解析 -
第12题:
单选题()孙悟空在烂桃山吃了几次桃子?A三
B五
C七
D九
正确答案: B解析: 暂无解析 -
第13题:
幼儿自编应用题“小华吃了7个桃子,一会儿又吃了6个桃子,他一共吃了儿个桃子?”存在的错误是()。A、被题目情节所吸引
B、条件不清楚
C、不符合生活逻辑
D、问题不明确
参考答案:C
-
第14题:
以下程序(程序左边的数字为附加的行号)______。1 include2 include 3 main()4 { 以下程序(程序左边的数字为附加的行号)______。 1 #include<str.h> 2 #include<stdio.h> 3 main() 4 { char s[]="string"; 5 puts(s); 6 strcpy(s,"hello"); 7 printf("%3s\n",s);}
A.没有错
B.第1行有错
C.第6行有错
D.第7行有错
正确答案:B
解析:字符串复制函数strcpy包含在头文件string.h中,因此,程序中的第1行文件包含命令是错误的。 -
第15题:
一群猴子分桃,桃子共有56个,每只猴子可以分到同样多的桃子。但在它们正要分桃时,又来了4只猴子,于是重新分配这些桃子,结果每只猴子分到的桃子数量相同,那么最后每只猴子分到多少个桃子?( )
A.6
B.7
C.8
D.9
正确答案:B
答案为7个。设刚开始有χ只猴子.则由题意可知,χ和χ+4都必定是56的公约数,故χ=4,则56÷(4+4)=7(个)。 -
第16题:
请教:2011年广西公务员考试《行测》标准预测试题(2)第1大题第12小题如何解答?【题目描述】
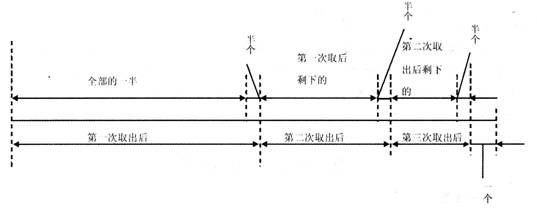
第 12 题有一筐西瓜,第一次取出全部的一半又半个,第二次取出剩下的一半又半个,第三次取出剩下的一半又半个,筐内还剩下一个西瓜。问:这个筐内原有西瓜多少个?( )

答案分析:正确答案:D
依题意可做图如下:
-
第17题:
某单位行政采购了一批水果作为员工的下午茶,共有若干箱苹果和桃子,苹果的箱数是桃 子箱数的 4 倍,如果每天吃 2 箱桃子和 6 箱苹果,那么桃子吃完时还剩 15 箱苹果。 该单位 采购了( )箱桃子。
A.15
B.20
C.30
D.60答案:A解析:因为苹果箱数是桃子的4倍,如果每天吃2箱桃子和8箱苹果,桃子和苹果可以同时吃完。现在每天少吃8-6=2箱苹果,还剩15箱苹果,因此吃了15÷2=7.5天,故桃子有2×7.5=15箱。 -
第18题:
熊大将自己栽种的一片桃树林承包给熊二,承包时桃树林已经结满桃子,熊大与熊二之间对桃子的归属没有约定,关于摘下来的桃子所有权的归属,下列表述正确的是( )。A.桃子的40%归熊大所有,60%归熊二所有
B.桃子全部归熊大所有
C.桃子全部归熊二所有
D.熊大和熊二各自享有50%的桃子答案:C解析:除法律另有规定或当事人另有约定外,所有权与用益物权分离的,孳息的所有权由用益物权人取得。本题中双方没有约定桃子的归属问题,桃子的所有权由用益物权人熊二取得。 -
第19题:
桃子可不可以与甲鱼一起吃?
正确答案: 桃子若与甲鱼(鳖)一起吃,容易出现腹泻;理由是,甲鱼为"滋腻"补品,本来就不好消化,桃子又容易导致胀气,两者相加,身体自然会感到不适。 -
第20题:
()吃了蟠桃园里的何种桃子便可以“成仙得道”?
- A、三千年一熟
- B、六千年一熟
- C、九千年一熟
- D、以上均对
正确答案:D -
第21题:
()孙悟空在烂桃山吃了几次桃子?
- A、三
- B、五
- C、七
- D、九
正确答案:C -
第22题:
多选题该市场桃子的供给弹性系数的含义是:价格上升1%时,桃子的供给量增加( )。A100吨
B10%
C1吨
D1%
正确答案: C,D解析:
农产品供给弹性系数反映的是价格变动1%,农产品供给量变动的百分比。该桃子的供给弹性为1,所以价格上升1%时,桃子的供给量增加1%。 -
第23题:
单选题在一堆桃子旁边住着5只猴子。深夜,第一只猴子起来偷吃了一个,剩下的正好平均分成5份,它藏起自己的一份,然后去睡觉。过了一会儿,第二只猴子起来也偷吃了一个,剩下的也正好平均分成5份,它也藏起自己的一份,然后去睡觉,第三个 .第四.五只猴子也都一次这样做。问那堆桃子最少有多少个?( )A4520
B3842
C3121
D2101
正确答案: A解析: -
第24题:
单选题()吃了蟠桃园里的何种桃子便可以“成仙得道”?A三千年一熟
B六千年一熟
C九千年一熟
D以上均对
正确答案: D解析: 暂无解析
