已知正态总体的数据出现在区间（-3，-1)里的概率和落在区间（3,5)里的概率相等，那么这个正态总体的数学期望为0

题目

已知正态总体的数据出现在区间（-3，-1)里的概率和落在区间（3,5)里的概率相等，那么这个正态总体的数学期望为0

相似考题

1.某样本数据在正态纸上描点,目测这些点在一直线附近,表示数据来自于正态总体,现从纵坐标轴上取概率为0.5,则其对应于近似直线上点的横坐标是正态总体________的估计。A．标准差σB．均值μC．μ+σD．μ+σ

2.根据概率论原理,正态母体落在区间的概率为()A、97.23%B、95.33%C、99.33%D、99.73%

3.正态概率纸可以用来( )。A.估计正态分布的均值B.判断数据是否来自二项分布的总体SXB正态概率纸可以用来（ ）。A.估计正态分布的均值B.判断数据是否来自二项分布的总体C.估计正态分布的方差D.判断数据是否来自正态分布的总体E.估计正态分布的标准

4.大样本资料，估计总体率的可信区间可用A、查表法B、正态近似法C、对数正态法D、百分位数法E、直接计算概率法

参考答案和解析
错误
更多“已知正态总体的数据出现在区间（-3，-1)里的概率和落在区间（3,5)里的概率相等，那么这个正态总体的数学期望为0”相关问题

  • 第1题：

    95%的置信水平是指()。

    A、总体参数落在一个特定的样本所构造的区间内的概率为95%

    B、在用同样方法构造的总体参数的多个区间中，包含总体参数的区间比率为95%

    C、总体参数落在一个特定的样本所构造的区间内的概率为5%

    D、在用同样方法构造的总体参数的多个区间中，包含总体参数的比率为5%


    参考答案：A

  • 第2题：

    正态总体参数均值、方差、标准差的1-α置信区间为( )。


    正确答案：ABDE
    解析：室正态总体均值、方差、标准差的1-α置信区间如表1.4-1所示。

  • 第3题：

    正态总体标准差σ的1 -a置信区间为（）（μ未知）。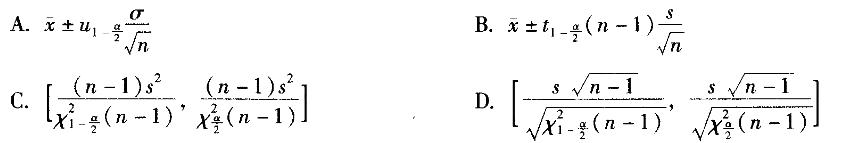


    答案：D
    解析：

  • 第4题：

    已知总体分布为正态，方差未知。从这个总体中随机抽取样本容量为65的样本，样本平均数 为60，样本方差为100，那么总体均值 的99%的置信区间为

    A.[ 56.775 ,63.225]
    B.[53.550,66.450]
    C.[56.080,63.920]
    D.[57.550,62.450]

    答案：A
    解析：
    本题考查的是总体平均数的估计方法。当总体方差未知时，若总体分布为正态，或者总体分布为非正态，但样本容量超过30，置信区间的公式是：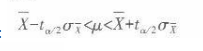

    因为总体方差未知，可通过如下公式计算标准误：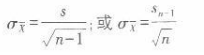

    当n>30时，t分布渐近正态分布，在不查表的情况下也可用

    作近似计算。将本题中各项数据代入，求得置信区间为[ 56.775，63.225]。因此本题选A。

  • 第5题：

    正态分布总体样本落在［μ－3δ，μ＋3δ］区间的概率为（）左右。

    • A、95.0%；
    • B、95.4%；
    • C、99.7%；
    • D、88.3%。

    正确答案:C

  • 第6题：

    对方差未知的正态总体进行样本容量相同的n次抽样，则这n个置信区间的宽度必然相等。


    正确答案:错误

  • 第7题：

    大样本资料，估计总体率的置信区间可用（）

    • A、查表法
    • B、正态近似法
    • C、对数正态法
    • D、百分位数法
    • E、直接计算概率法

    正确答案:B

  • 第8题：

    以下问题可以用Z检验的有（）。

    • A、正态总体均值的检验，方差已知
    • B、正态总体均值的检验，方差未知
    • C、大样本下总体均值的检验
    • D、正态总体方差的检验

    正确答案:A,C

  • 第9题：

    满足什么条件时可以采取正态近似法估计总体概率的置信区间？


    正确答案: 当n足够大，且样本频率p和1—p均不太小时，如np与n（1—p）均大于5时，可用正态近似法求总体概率的置信区间。

  • 第10题：

    单选题
    对于正态随机变量来说，它落在区间（μ-3σ，μ+3α）外的概率为（）。
    A

    99.73%

    B

    68.26%

    C

    4.55%

    D

    0.27%


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    95%的置信水平是指（　　）。
    A

    总体参数落在一个特定的样本所构造的区间内的概率为95%

    B

    总体参数落在一个特定的样本所构造的区间内的概率为5%

    C

    在用同样方法构造的总体参数的多个区间中，包含总体参数的区间比例为95%

    D

    在用同样方法构造的总体参数的多个区间中，包含总体参数的区间比例为5%


    正确答案： D
    解析：
    对于置信区间的理解，要注意：①置信水平为95%的置信区间指在用某种方法构造的所有区间中，有95%的区间包含总体参数的真值，5%的区间不包含总体参数的真值；②总体参数的真值是固定的，未知的，而样本构造的区间则是不固定的。置信区间是一个随机区间；③95%这个概率不是用来描述某个特定的区间包含总体参数真值可能性的，而是针对随机区间而言的。

  • 第12题：

    单选题
    正态均值90%的置信区间是从13.8067至18.1933，以下解读正确的是：（）。
    A

    均值落在13.8067至18.1933范围内的概率是90%

    B

    总体中所有值的90%落在13.8067至18.1933

    C

    总体中所有样本值的90%落在13.8067至18.1933

    D

    置信区间变差均值的概率为90%


    正确答案： D
    解析： 暂无解析

  • 第13题：

    在均数为0，标准差为σ的正态总体中随机抽样，统计量| |大于以下哪一项的概率为0.05


    正确答案：B
    (答案：B)因为服从均数为0，标准差为(作图)的正态分布，根据u变换，服从标准正态分布，则即P。因为，所以。

  • 第14题：

    正态总体标准差σ的1-α置信区间为( )(μ未知)。


    正确答案：D
    解析：σ2的估计常用样本方差s2，因此从s2的分布来构造置信区间。利用χ2(n-1)分布可以得到σ2的1-α置信区间为：，其中与分别是χ2(n-1)分布的分位数与分位数。将上式两边开平方，可得σ的1-α置信区间为。

  • 第15题：

    设正态总体X的方差为1,根据来自总体X的容量为100的简单随机样本测得样本的均值为5,则总体X的数学期望的置信度近似等于0.95的置信区间为_______.


    答案：1、(4.804 2、5.196)
    解析：
    X～N（μ，1），取统计量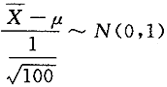，则μ的置信度为0.95的置信区间为　　

  • 第16题：

    已知总体分布为正态，方差为100。从这个总体中随机抽取样本容量为16的样本，样本平均数为60，那么总体均值 的99%的置信区间为

    A.[50.10,69.90]
    B.[53.55,66.45]
    C.[56.08,63.92]
    D.[55.10,64.90]

    答案：B
    解析：
    本题考查的是总体平均数的估计方法。当总体方差已知时，若总体分布为正态，或者总体分布为非正态，但样本容量超过30，置信区间的公式是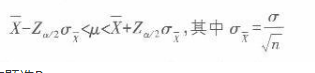

    将本题中各项数据代入，则求得置信区间为[ 53.55，66.45]。

  • 第17题：

    对于正态随机变量来说，它落在区间（μ-3σ，μ+3α）外的概率为（）。

    • A、99.73%
    • B、68.26%
    • C、4.55%
    • D、0.27%

    正确答案:C

  • 第18题：

    一个95%的置信区间是指（）

    • A、总体参数有95%的概率落在这一区间内
    • B、总体参数有5%的概率未落在这一区间内
    • C、在用同样方法构造的总体参数的多个区间中，有95%的区间包含该总体参数
    • D、在用同样方法构造的总体参数的多个区间中，有95%的区间不包含该总体参数

    正确答案:C

  • 第19题：

    当正态总体的方差已知时，估计总体均值的置信区间使用的分布是（）。

    • A、正态分布
    • B、t分布
    • C、卡方分布
    • D、F分布

    正确答案:A

  • 第20题：

    正态均值的90%的置信区间是从13.8067至18.1933。这个意思是：（）

    • A、均值落在13.8067至18.1933范围内的概率是90%
    • B、总体中所有值的90%落在13.8067至18.1933
    • C、总体中所有样本值的90%落在13.867至13.1933
    • D、置信区间变差均值的概率为90%

    正确答案:C

  • 第21题：

    当你执行样本的正态性检验时，P值为0.75时，下面说法正确的是（）

    • A、该数据不是连续性数据
    • B、该数据不能判定是否正态
    • C、该数据是正态的
    • D、该数据代表的总体符合规格的概率为75%

    正确答案:C

  • 第22题：

    单选题
    当你执行样本的正态性检验时，P值为0.75时，下面说法正确的是（）
    A

    该数据不是连续性数据

    B

    该数据不能判定是否正态

    C

    该数据是正态的

    D

    该数据代表的总体符合规格的概率为75%


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    正态均值的90%的置信区间是从13.8067至18.1933。这个意思是：（）
    A

    均值落在13.8067至18.1933范围内的概率是90%

    B

    总体中所有值的90%落在13.8067至18.1933

    C

    总体中所有样本值的90%落在13.867至13.1933

    D

    置信区间变差均值的概率为90%


    正确答案： B
    解析： 暂无解析

  • 第24题：

    单选题
    大样本资料，估计总体率的置信区间可用（）
    A

    查表法

    B

    正态近似法

    C

    对数正态法

    D

    百分位数法

    E

    直接计算概率法


    正确答案： C
    解析： 暂无解析

相关内容