函数y=ex+arctanx在区间[-1，1]上( )A.单调减少 B.单调增加 C.无最大值 D.无最小值

题目
函数y=ex+arctanx在区间[-1，1]上( )

A.单调减少
B.单调增加
C.无最大值
D.无最小值
相似考题

1.函数y=3x^2－x^3在区间[1,3]上的最大值为()A、4B、0C、1D、3

2.已知函数f（x）=x3 +ax2+b，曲线y=f（x）在点（1，1）处的切线为y=x．（I）求a，b；（II）求f（x）的单调区间，并说明它在各区间的单调性．

3.在区间(－1,0)上由()给出的函数是单调增加的。A、y=∣x∣+1B、y=5x-2C、y=-4x+3D、y=∣x∣-2x

4.函数y=ln(1＋x^2)在区间[－2,－1]上的最大值为()A、4B、0C、1D、ln5

更多“函数y=ex+arctanx在区间[-1，1]上( )”相关问题

  • 第1题：

    函数y=(x-2)2在区间[0,4]上的最小值是_________.


    正确答案：
    0

  • 第2题：

    区间[a,b]上的三次样条插值函数是()

    A、在[a,b]上2阶可导，节点的函数值已知，子区间上为3次多项式

    B、在区间[a,b]上连续的函数

    C、在区间[a,b]上每点可微的函数

    D、在每个子区间上可微的多项式


    参考答案：A

  • 第3题：

    函数f(x)=x3在闭区间[-1，1]上的最大值为_______.


    答案：
    解析：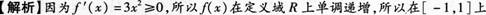


    也单调递增，故最大值在X=1处取得，即为f(1)=1.

  • 第4题：

    二次函数y＝2x2＋mx－5在区间(－∞，－1)内是减函数，在区间(－1，＋∞)内是增函数，则m的值是（　　）

    A.4
    B.－4
    C.2
    D.－2

    答案：A
    解析：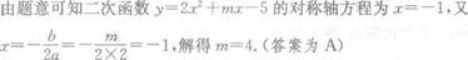

  • 第5题：

    若函数y=(x)在[-1，1]上是单调函数，则使得y=(sinx)必为单调函数的区间是（ ）

    A.R
    B.[-1，1]
    C.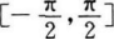
    D.[-sin1，sin1]


    答案：C
    解析：
    【考情点拨】本题主要考查的知识点为函数的单调区间． 1应试指导】y=(x)在[-1，1]上是单调函数，∴y=(x)的单调区间为[-1，1]，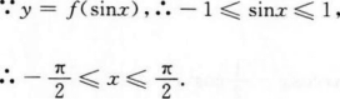

  • 第6题：

    如图，连续函数y＝f(x)在区间[一3，一2]，[2，3]上的图形分别是直径为l的上、下半圆周，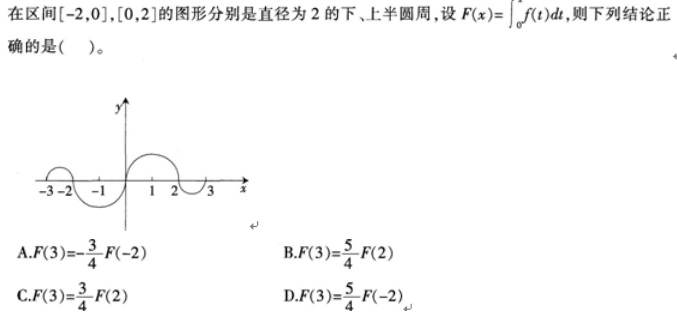


    答案：C
    解析：

  • 第7题：

    函数y=x2-x+1在区间[-1，3]上满足拉格朗日中值定理的ξ=（　　）


    答案：D
    解析：
    y=x2-x+1在[-1，3]上满足拉格朗日中值定理，

  • 第8题：

    求函数y=x-lnx的单调区间，并求该曲线在点(1，1)处的切线l的方程．


    答案：
    解析：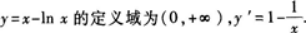


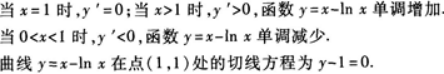
    【评析】求函数f(x)的单调区间，应先判定函数的定义域．求出函数的驻点，即y′=0的点；求出y的不可导的点，再找出y′>0时x的取值范围，这个范围可能是一个区间，也可能为几个区间．

  • 第9题：

    函数y=x2-2x在区间[2，3]上的最大值是( )。

    A.0
    B.3
    C.4
    D.5

    答案：B
    解析：
    函数的开口向上，对称轴为x=1，可知函数在区间[2，3]上单调递增，在此区间上的最大值在x=3处取得，为3，选择B。

  • 第10题：

    单选题
    奇函数f（x）在闭区间[－1，1]上可导，且|f′（x）|≤M（M为正常数），则必有（　　）。
    A

    ｜f（x）｜≥M

    B

    ｜f（x）｜＞M

    C

    ｜f（x）｜≤M

    D

    ｜f（x）｜＜M


    正确答案： D
    解析：
    因为f（x）为奇函数，故f（0）＝0。f（x）在[－1，1]上可导，由拉格朗日中值定理知|f（x）|＝|f（x）－f（0）|＝|f′（ξ）|·|x－0|≤M·1。故对∀x∈[－1，1]，|f（x）|≤M。故应选（C）。

  • 第11题：

    单选题
    设P(x)是在区间[α,b]上的y=f(x)川的分段线性插值函数,以下条件中不是P(x)必须满足的条件为（　）。
    A

    P(x)在[a,b]上连续

    B

    P(Xk)=Yk

    C

    P(x)在[α,b]上可导

    D

    P(x)在各子区间上是线性函数


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    x－y＝0

    B

    x＋y＝0

    C

    －x－y＝0

    D

    －x＋y＝0


    正确答案： C
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第13题：

    在(－1,1)区间上满足罗定理条件的函数是()

    A、y=x

    B、y=1/x

    C、y=x²

    D、y=/x/


    答案：C
    解析：A.函数在区间两端点的值不相等,即f(-1)≠f(1)，错误
    B.函数在[-1,1]上不连续，错误
    D错，x=0时不可导
    所以选C。


  • 第14题：

    函数曲线y＝1n(1＋x2)的凹区间是（）

    A.(－1，1)
    B.(－∞，－1)
    C.(1，＋∞)
    D.(－∞，＋∞)

    答案：A
    解析：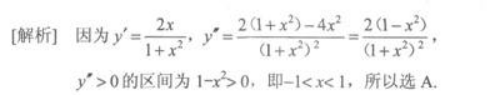

  • 第15题：

    幂级数在区间(-1，1)内的和函数S(x)=________.


    答案：
    解析：

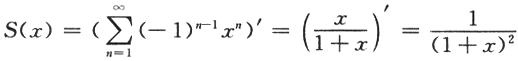
  • 第16题：

    若函数y=f（z）在[a，b]上单调，则使得y=f（x+3）必为单调函数的区间是（　　）

    A.[a，b+3]
    B.[a+3，b+3]
    C.[a一3，b—3]
    D.[a+3，b]

    答案：C
    解析：

  • 第17题：

    函数级数的收敛区间为( )。

    A、(一1，1)
    B、(1,1]
    C、[一1，1)
    D、[-1，1]

    答案：A
    解析：
    由已知得级数的收敛半径为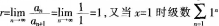发散，当x=-l时级数发散，故选A。

  • 第18题：

    函数y=sinx在区间[0，π]上满足罗尔定理的ξ=（　　）


    答案：C
    解析：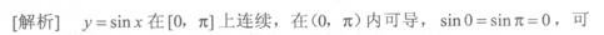

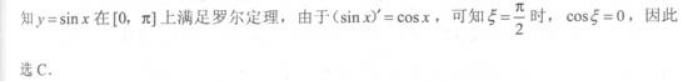
  • 第19题：

    函数f(x)=5x在区间[-1，1]上的最大值是（）

    A.-1/5
    B.0
    C.1/5
    D.5

    答案：D
    解析：
    f(x)=5x，f'(x)=5xln5>0，可知f(x)在[-1，1]上单调增加，最大值为f(1)=5，所以选D．

  • 第20题：

    奇函数f（x）在闭区间[-1，1]上可导，且f′（x）≤M（M为正常数），则必有（ ）《》（ ）

    A.f（x）≥M
    B.f（x）＞M
    C.f（x）≤M
    D.f（x）＜M

    答案：C
    解析：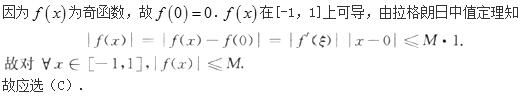

  • 第21题：

    反正切函数y=arctgx的定义域是（）。

    • A、[0，π]
    • B、[-π/2，π/2]
    • C、[-1，1]
    • D、全部实数

    正确答案:D

  • 第22题：

    填空题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为____。

    正确答案： x-y=0
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第23题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    －x－y＝0

    B

    x－y－1＝0

    C

    x－y＝0

    D

    x＋y＝0


    正确答案： A
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

相关内容