由曲线y=x2，直线y=a，x=0及x=1所围成的图形如图3—4中阴影部分所示，其中0≤a≤1．(1)求图中阴影部分的面积A． (2)问a为何值时，A的取值最小，并求出此最小值．

题目
由曲线y=x2，直线y=a，x=0及x=1所围成的图形如图3—4中阴影部分所示，其中0≤a≤1．

(1)求图中阴影部分的面积A．
(2)问a为何值时，A的取值最小，并求出此最小值．

相似考题

1.设平面区域D由曲线y=1／x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。

2.曲线y=x2与y=4—x2所围成的图形的面积为_________．

3.由曲线和直线x=1，x=2，y= -1围成的图形，绕直线：y= -1旋转所得旋转体的体积为：

4.由曲线y=x3，y=0，x=－1，x=l所围图形的面积为____。

更多“由曲线y=x2，直线y=a，x=0及x=1所围成的图形如图3—4中阴影部分所示，其中0≤a≤1． ”相关问题

  • 第1题：

    由曲线y=ex，y=e-2x及直线x=-1所围成图形的面积是：


    答案：B
    解析：
    提示：画图分析围成平面区域的曲线位置关系，得到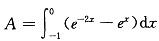计算出结果。

  • 第2题：

    由抛物线y=x2与三直线x=a，x=a+1，y=0所围成的平面图形，a为下列（　　）值时图形的面积最小。


    答案：B
    解析：
    平面图形的面积

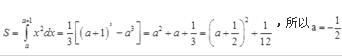
    时图形面积最小。

  • 第3题：

    由曲线y=x2/2和直线x=1，x=2，y=-1围成的图形，绕直线y=-1旋转所得旋转体的体积为：
    A.(293/60)π B.π/60 C. 4π2 D. 5π


    答案：A
    解析：
    提示:画出平面图形，列出绕直线y=-1旋转的体积表达式，注意旋转体的旋转半径为x2/2- (-1)。计算如下：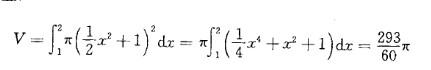

  • 第4题：

    ①求由曲线y=x，y=1/x，x=2与y=0所围成的平面图形的面积S；
    ②求①中的平面图形绕x轴旋转一周所得旋转体的体积V．


    答案：
    解析：
    ①如图1—3-6所示，由已知条件可得

  • 第5题：

    设D为曲线y=1-x2，直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·
    ①求平面图形的面积；
    ②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．


    答案：
    解析：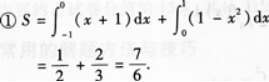

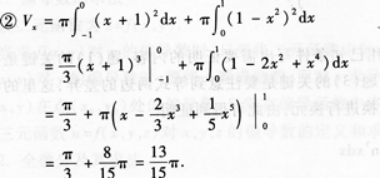
  • 第6题：

    求曲线y=x2与直线y=0，x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积．


    答案：
    解析：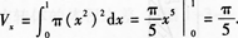

  • 第7题：

    D域由x轴、x2+y2-2x=0(y≥0)及x+y=2 所围成，f(x,y)是连续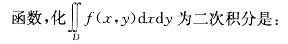



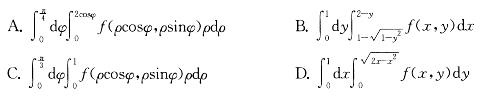    答案：B
    解析：
    提示 x2+y2-2x=0，(x-1)2+y2 =1，D由(x-1)2+y2 =1，(y≥0)，x+y =2与x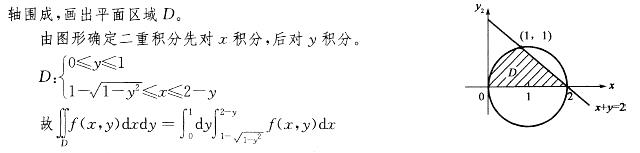

  • 第8题：

    曲线y=sinx(0≤x≤π/2)与直线x=π/2,y=0围成的平面图形绕x轴旋转产生的旋转体体积是()。


    答案：A
    解析：
    提示：利用旋转体体积公式

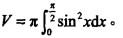
  • 第9题：

    求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积·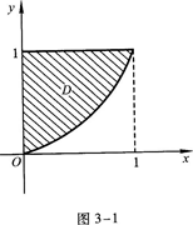


    答案：
    解析：
    y=x2(x≥0)，y=1及y轴围成的平面图形D如图3—1所示．其面积为

  • 第10题：

    由曲线y=x2／2和直线x=1，x=2，y=-1围成的图形，绕直线y=-1旋转所得旋转体体积为：（）

    • A、（293／60）π
    • B、π／60
    • C、4π2
    • D、5π

    正确答案:A

  • 第11题：

    单选题
    由抛物线y=x2与三直线x=a，x=a+1，y=0围成平面图形。问a为何值时图形的面积最小？（）
    A

    1

    B

    -1／2

    C

    0

    D

    2


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    垂直于x轴的动直线与过原点的曲线y=y（x）（x≥0，y≥0）以及x轴围成一个以［0，x］为底边的曲边梯形，其面积为y3（x）．函数y（x）的隐函数形式是（）．
    A

    y2-x=0

    B

    y2+x=0

    C

    3y2-2x=0

    D

    2y-3x2=0


    正确答案： C
    解析： 暂无解析

  • 第13题：

    D 域由 x 轴，x2 + y2 ? 2x = 0( y ≥ 0)及 x+y=2 所围成， f (x, y)是连续函数，化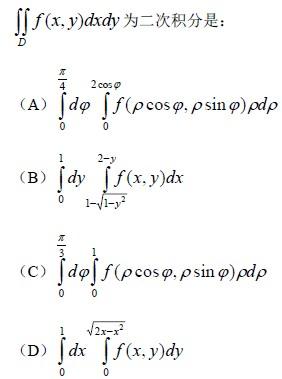


    答案：B
    解析：
    解：选 B。
    画积分区域如下图所示，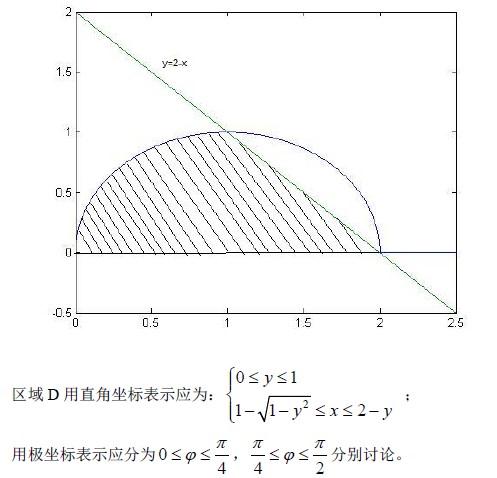

  • 第14题：

    设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

    A．2x-y+2=0
    B．2x+y+1=0
    C．2x+y-3=0
    D．2x-y+3=0

    答案：D
    解析：


    @##

  • 第15题：

    设曲线y=4-x2(x≥0)与x轴，y轴及直线x=4所围成的平面图形为D(如
    图1—3—2中阴影部分所示)．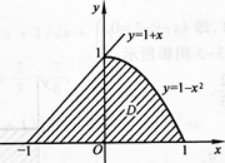

    图1—3—1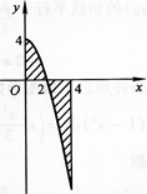

    图1—3—2
    ①求D的面积S；
    ②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy．


    答案：
    解析：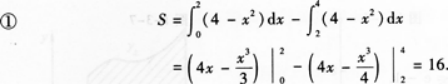

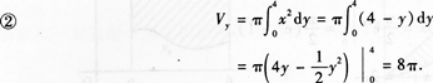
  • 第16题：

    ①求曲线y=x2(x≥0)，y=1与x=0所围成的平面图形的面积S：
    ②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy．


    答案：
    解析：
    ①由已知条件画出平面图形如图l—3-5阴影所示．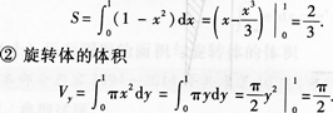

    图1—3—5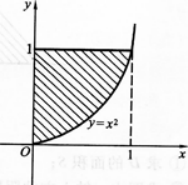

  • 第17题：

    ①求曲线y=ex及直线x=1，x=0，y=0所围成的图形D的面积S：
    ②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．


    答案：
    解析：
    画出平面图形如图l一3-7阴影所示．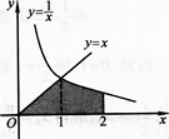
    图1—3—6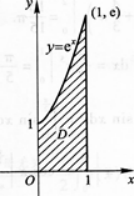

    图1—3—7

  • 第18题：

    曲线Y=x2，x=0，x=2，Y=0所围成的图形的面积为（　　）．



    答案：B
    解析：
    如右图所示，阴影部分的面积即为所求，由定积分的几何


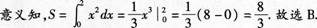
  • 第19题：

    设f（x）为区间[a，b]上的连续函数，则曲线y=f（x）与直线x=a，x=b，y=0所围成的封闭图形的面积为（ ）.《》（ ）


    答案：B
    解析：
    本题考查的知识点为定积分的几何意义.由定积分的几何意义可知应选B.常见的错误是选C.如果画个草图，则可以避免这类错误.

  • 第20题：

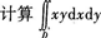    ，其中区域如图5-3所示，由y=x，y=1与Y轴围成．


    答案：
    解析：
    将所给积分化为二次积分．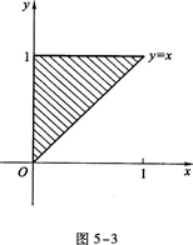

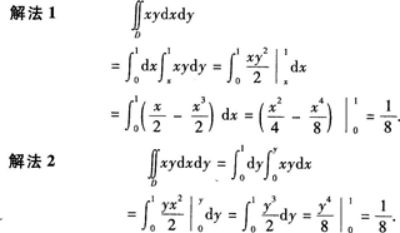
  • 第21题：

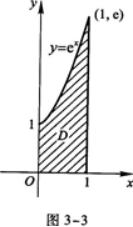
    (1)求曲线Y=ex及直线x=1，x=0,y=0所围成的平面图形(如图3—3所示)
    的面积A．
    (2)求(1)中平面图形绕x轴旋转一周所得旋转体的体积Vx.


    答案：
    解析：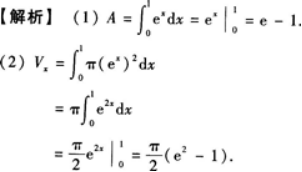

  • 第22题：

    由抛物线y=x2与三直线x=a，x=a+1，y=0围成平面图形。问a为何值时图形的面积最小？（）

    • A、1
    • B、-1／2
    • C、0
    • D、2

    正确答案:B

  • 第23题：

    单选题
    由曲线y=x2／2和直线x=1，x=2，y=-1围成的图形，绕直线y=-1旋转所得旋转体体积为：（）
    A

    （293／60）π

    B

    π／60

    C

    4π2

    D

    5π


    正确答案： D
    解析： 暂无解析

相关内容