设二元函数z=xy，则点Po(0，0)（）A.为z的驻点，但不为极值点 B.为z的驻点，且为极大值点 C.为z的驻点，且为极小值点 D.不为z的驻点，也不为极值点

题目
设二元函数z=xy，则点Po(0，0)（）

A.为z的驻点，但不为极值点
B.为z的驻点，且为极大值点
C.为z的驻点，且为极小值点
D.不为z的驻点，也不为极值点
相似考题

1.(本题满分6分)设函数z=sin(xy)+2x2+y，求dz．

2.对于函数z＝xy，原点(0，0)（ ）A．不是驻点B．是驻点但非极值点C．是驻点且为极大值点D．是驻点且为极小值点

3.下面关于函数依赖的叙述中，不正确的是（ ）。A)若XY→Z，则X→Z，Y→ZB)若X→Y，X→Z，则X→YZC)若X→Y，则XZ→YZD)若X→Y，WY→Z，则XW→Z

4.设函数z=cos(x2+y2)，则(δz/δx) _______．

更多“设二元函数z=xy，则点Po(0，0)（）”相关问题

  • 第1题：

    下列关于函数依赖的规则中，哪一条是正确的?______。

    A．若X→Y，WY→Z，则XW→Z

    B．若X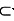Y，则X→Y

    C．若XY→Z，则X→Z,Y→Z

    D．若X∩Y=Φ，则X→Y


    正确答案：A

  • 第2题：

    下面关于函数依赖的叙述中，正确的是（ ）。

    Ⅰ.若X→Y，X→Z，则X→YZⅡ.若XY→Z，则x→Z，Y→Z

    Ⅲ.若X→Y，WY→Z，则X→ZⅣ.若X→Y，Y→Y’，则X→Y’


    正确答案：B
    根据函数依赖的几个概念和Armstrong公理系统的推理规则来逐个判断。

  • 第3题：

    设z=xy，则dz=()

    A.yxy-1dx+xyInxdy
    B.xy-1dx+ydy
    C.xy(dx+dy)
    D.xy(xdx+ydy)

    答案：A
    解析：
    【考情点拨】本题考查了二元函数的全微分的知识点【应试指导】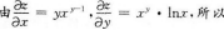

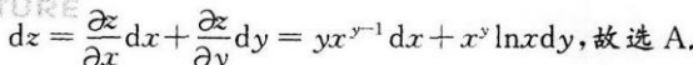
  • 第4题：

    对于函数z=xy，原点(0，0)（）

    A.不是函数的驻点
    B.是驻点不是极值点
    C.是驻点也是极值点
    D.无法判定是否为极值点

    答案：B
    解析：
    【考情点拨】本题考查了函数的驻点、极值点的知识点．

  • 第5题：

    设函数，(u)可导，z=f(sin y-sin x)+xy，则=__________.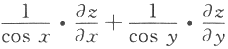


    答案：
    解析：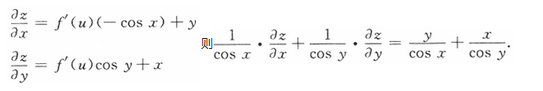

  • 第6题：

    设函数z=xy，则全微分dz_______.


    答案：
    解析：

  • 第7题：

    在XOY坐标面中，函数z=ln|x-y|的间断点只有（0，0）点。


    正确答案:错误

  • 第8题：

    函数f（x，y）=xy（6-x-y）的极值点是（）．

    • A、（0，0）
    • B、（6，0）
    • C、（0，6）
    • D、（2，2）

    正确答案:D

  • 第9题：

    单选题
    若二元函数z=arctg（xy），则z（x，y）关于x的偏导数在（1，1）点的值是（）。
    A

    1/2

    B

    1

    C

    2

    D

    0


    正确答案： B
    解析： 暂无解析

  • 第10题：

    填空题
    设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝____。

    正确答案： yf1′+f2′/y-yg′/x2
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f1′y＋f2′·（1/y）＋g′·（－y/x2）＝f1′y＋f2′/y－yg′/x2。

  • 第11题：

    填空题
    设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝____。

    正确答案： 2(-yf1′/x+xf2′/y)
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f1′·（－y/x2）＋f2′·（1/y），∂z/∂y＝f1′·（1/x）＋f2′·（－x/y2），x∂z/∂x－y∂z/∂y＝2（－yf1′/x＋xf2′/y）。

  • 第12题：

    单选题
    若z=xy+sinxy则函数z（x，y）在（0，1）点关于x的偏导数的值是（）。
    A

    0

    B

    2

    C

    1

    D

    -1/2


    正确答案： B
    解析： 暂无解析

  • 第13题：

    下列关于函数依赖的规则中，正确的是( )。

    A．若X→Y，WY→Z，则XY→Z

    B．若X∩Y=，则X→Y

    C．若XY→Z 则X→Z，Y→Z

    D．若YZ， 则Y→Z


    正确答案：A
    解析：根据函数依赖的几个概念和Armstrong公理系统的推理规则来逐个判断。Armstrong公理系统包括3条推理规则：①自反律。若YXU，则X→Y为F所逻辑蕴含。②增广律。若X→Y为F所逻辑蕴含，且ZU，则XZ→YZ为F所逻辑蕴含。③传递律。若X→Y及Y→Z为F所逻辑蕴含，则X→Z为F所逻辑蕴含。根据以上3条推理规则可以得到以下3条有用的规则：①合并规则。由X→Y，X→Z，有X→YZ。②伪传递规则。由X→Y，WY→Z，有XW→Z。③分解规则。由X→Y及ZY，有X→Z。根据伪传递规则，选项A)是正确的。选项C)是错误的，因为在函数依赖关系中，决定因素的某个真子集不一定能确定一个函数依赖关系。选项B)和D)更是错误。

  • 第14题：

    设函数f(x，y)在点(0，0)的某邻域内有定义，且fx(0，0)=3，fy(0，0)=-1，则有( ).

    A.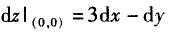
    B.曲面z=f(x，y)在点(0，0，f(0，0))的一个法向量为3i-j+k
    C.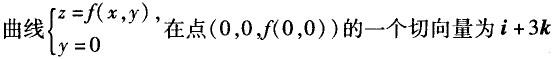
    D.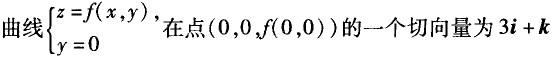

    答案：C
    解析：
    A不成立，因为可偏导未必可微分； B 不成立，一个法向量应为3i-j-k，取x为参数，则曲线x=x，y=0，z=f(x，0)在点(0，0，f(0，0))处的切向量为i+3k，故得 C

  • 第15题：

    设z=xy，则dz=（）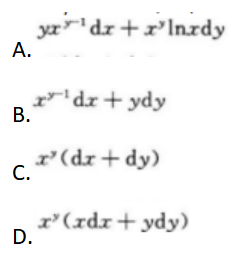


    答案：A
    解析：
    【考情点拨】本题考查了二元函数的全微分的知识点．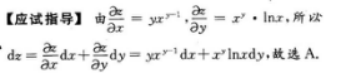

  • 第16题：

    设函数f(μ，ν)具有二阶连续偏导数，z=f(x，xy)，则=________.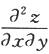


    答案：
    解析：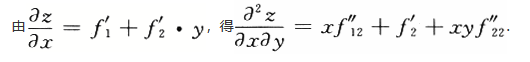

  • 第17题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第18题：

    设函数f（x，y）＝x3+y3-3xy，则（）。

    • A、f（0，0）为极大值
    • B、f（0，0）为极小值
    • C、f（1，1）为极大值
    • D、f（1，1）为极小值

    正确答案:D

  • 第19题：

    若二元函数z=arctg（xy），则z（x，y）关于x的偏导数在（1，1）点的值是（）。

    • A、1/2
    • B、1
    • C、2
    • D、0

    正确答案:A

  • 第20题：

    若z=xy+sinxy则函数z（x，y）在（0，1）点关于x的偏导数的值是（）。

    • A、0
    • B、2
    • C、1
    • D、-1/2

    正确答案:B

  • 第21题：

    填空题
    设二元函数z＝xex＋y＋（x＋1）ln（1＋y），则dz|（1，0）＝____。

    正确答案： 2edx+(e+2)dy
    解析：
    由二元函数z＝xex＋y＋（x＋1）ln（1＋y）得∂z/∂x＝ex＋y＋xex＋y＋ln（1＋y），∂z/∂y＝xex＋y＋（x＋1）/（1＋y），故有∂z/∂x|（1，0）＝2e，∂z/∂y|（1，0）＝e＋2，dz|（1，0）＝2edx＋（e＋2）dy。

  • 第22题：

    单选题
    设z＝z（x，y）是由方程xz－xy＋ln（xyz）＝0所确定的可微函数，则∂z/∂y等于（　　）。[2013年真题]
    A

    －xz/（xz＋1）

    B

    －x＋1/2

    C

    z（－xz＋y）/[x（xz＋1）]

    D

    z（xy－1）/[y（xz＋1）]


    正确答案： B
    解析：
    将xz－xy＋ln（xyz）＝0两边对y求偏导，得xzy′－x＋x（z＋y·zy′）/（xyz）＝0，整理得zy′＝z（xy－1）/[y（xz＋1）]。

  • 第23题：

    单选题
    设函数z＝f（x，y）的全微分为dz＝xdx＋ydy，则点（0，0）（　　）。
    A

    不是f（x，y）的连续点

    B

    不是f（x，y）的极值点

    C

    是f（x，y）的极大值点

    D

    是f（x，y）的极小值点


    正确答案： D
    解析：
    函数的全微分为dz＝xdx＋ydy，则∂z/∂x＝x，∂z/∂y＝y，故∂2z/∂x2|（0，0）＝1＝A，∂2z/∂x∂y|（0，0）＝0＝B，∂2z/∂y2|（0，0）＝1＝C，又∂z/∂x|（0，0）＝0，∂z/∂y|（0，0）＝0，则B2－AC＝－1＜0，A＞0。故（0，0）是函数f（x，y）的极小值点。

相关内容