设函数z=ln(x+y2),则全微分dz=_______.
题目
设函数z=ln(x+y2),则全微分dz=_______.
相似考题
更多“设函数z=ln(x+y2),则全微分dz=_______.”相关问题
-
第1题:
设z=xy,则dz=()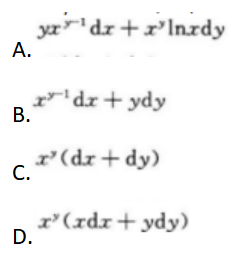 答案:A解析:【考情点拨】本题考查了二元函数的全微分的知识点.
答案:A解析:【考情点拨】本题考查了二元函数的全微分的知识点.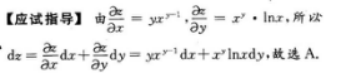
-
第2题:
设z=z(x,y)是由方程x2+y2+z2=ez所确定的隐函数,求dz.答案:解析:
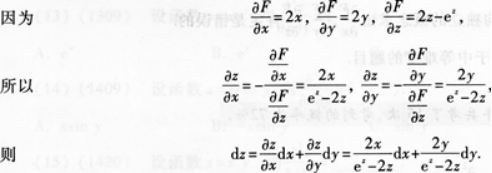
-
第3题:
设函数z=ex+y,则dz=_______.答案:解析:填exdx+dy. -
第4题:
设函数z=e2x+y则全微分出dz=______.答案:解析: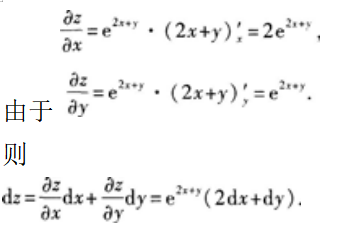
-
第5题:
设函数z=3x+y2,则dz=__________.答案:解析:3dx+2ydy -
第6题:
对于二元函数z=f(x,y),下列有关偏导数与全微分关系中正确的命题是()。
- A、偏导数存在,则全微分存在
- B、偏导数连续,则全微分必存在
- C、全微分存在,则偏导数必连续
- D、全微分存在,而偏导数不一定存在
正确答案:B -
第7题:
函数z=xy2+y(lny-1)在x=1,y=1处的全微分dz等于().
- A、dx+dy
- B、dx-dy
- C、dx+2dy
- D、dx-2dy
正确答案:C -
第8题:
填空题设函数f(u)可微,且f′(0)=1/2,则z=f(4x2-y2)在点(1,2)处的全微分dz|(1,2)=____。正确答案: 4dx-2dy解析:
求全微分,即需求出函数对各个自变量的偏导。令u=4x2-y2,则∂z/∂x=f′(u)·∂u/∂x=f′(u)·8x,∂z/∂y=f′(u)·∂u/∂y=f′(u)·(-2y),将(1,2)代入u=4x2-y2得u=0,又f′(0)=1/2,故dz|(1,2)=f′(0)·8dx+f′(0)·(-2·2)dy=4dx-2dy。 -
第9题:
单选题函数z=xy2+y(lny-1)在x=1,y=1处的全微分dz等于().Adx+dy
Bdx-dy
Cdx+2dy
Ddx-2dy
正确答案: A解析: 暂无解析 -
第10题:
单选题设z=z(x,y)是由方程xz-xy+ln(xyz)=0所确定的可微函数,则∂z/∂y等于( )。[2013年真题]A-xz/(xz+1)
B-x+1/2
Cz(-xz+y)/[x(xz+1)]
Dz(xy-1)/[y(xz+1)]
正确答案: B解析:
将xz-xy+ln(xyz)=0两边对y求偏导,得xzy′-x+x(z+y·zy′)/(xyz)=0,整理得zy′=z(xy-1)/[y(xz+1)]。 -
第11题:
单选题设函数z=f(x,y)的全微分为dz=xdx+ydy,则点(0,0)( )。A不是f(x,y)的连续点
B不是f(x,y)的极值点
C是f(x,y)的极大值点
D是f(x,y)的极小值点
正确答案: D解析:
函数的全微分为dz=xdx+ydy,则∂z/∂x=x,∂z/∂y=y,故∂2z/∂x2|(0,0)=1=A,∂2z/∂x∂y|(0,0)=0=B,∂2z/∂y2|(0,0)=1=C,又∂z/∂x|(0,0)=0,∂z/∂y|(0,0)=0,则B2-AC=-1<0,A>0。故(0,0)是函数f(x,y)的极小值点。 -
第12题:
单选题若z=sin(xy)则它的全微分dz=()。Axcos(xy)
B(xdx+ydy)cos(xy)
Cycos(xy)
D(ydx+xdy)cos(xy)
正确答案: D解析: 暂无解析 -
第13题:
设函数y=ln(1+x),则y"=_____.答案:解析:

-
第14题:
设函数z=ln(x+y),则全微分dz=________.答案:解析: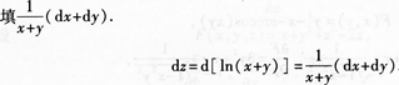
-
第15题:
若函数z=ln(xy)/y,则当x=e,y=e-1时,全微分dz等于( )。
A. edx + dy B. e2dx-dy C. dx + e2dy D. edx+e2dy答案:C解析:正确答案是C。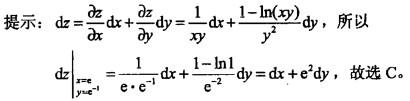
-
第16题:
设Z=Z(x,Y)是由方程x+y3+z+e2=1确定的函数,求dz答案:解析:利用隐函数求偏导数公式,记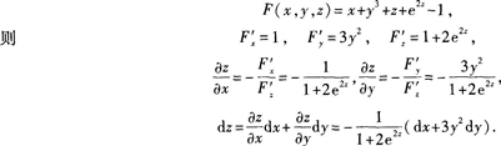
-
第17题:
设函数z=xy,则全微分dz_______.答案:解析:
-
第18题:
若z=sin(xy)则它的全微分dz=()。
- A、xcos(xy)
- B、(xdx+ydy)cos(xy)
- C、ycos(xy)
- D、(ydx+xdy)cos(xy)
正确答案:D -
第19题:
单选题设函数f(u)可微,且f′(0)=1/2,则z=f(4x2-y2)在点(1,2)处的全微分dz|(1,2)=( )。A4dx+2dy
B4dx-2dy
C-4dx+2dy
D-4dx-2dy
正确答案: A解析:
求全微分,即需求出函数对各个自变量的偏导。令u=4x2-y2,则∂z/∂x=f′(u)·∂u/∂x=f′(u)·8x,∂z/∂y=f′(u)·∂u/∂y=f′(u)·(-2y),将(1,2)代入u=4x2-y2得u=0,又f′(0)=1/2,故dz|(1,2)=f′(0)·8dx+f′(0)·(-2·2)dy=4dx-2dy。 -
第20题:
填空题设二元函数z=xex+y+(x+1)ln(1+y),则dz|(1,0)=____。正确答案: 2edx+(e+2)dy解析:
由二元函数z=xex+y+(x+1)ln(1+y)得∂z/∂x=ex+y+xex+y+ln(1+y),∂z/∂y=xex+y+(x+1)/(1+y),故有∂z/∂x|(1,0)=2e,∂z/∂y|(1,0)=e+2,dz|(1,0)=2edx+(e+2)dy。 -
第21题:
单选题设方程x2+y2+z2=4z确定可微函数z=z(x,y),则全微分dz等于( )。[2014年真题]A(ydx+xdy)/(2-z)
B(xdx+ydy)/(2-z)
C(dx+dy)/(2+z)
D(dx-dy)/(2-z)
正确答案: C解析:
对等式两边分别同时求导,得:2xdx+2ydy+2zdz=4dz。所以dz=(xdx+ydy)/(2-z) -
第22题:
单选题对于二元函数z=f(x,y),下列有关偏导数与全微分关系中正确的命题是()。A偏导数存在,则全微分存在
B偏导数连续,则全微分必存在
C全微分存在,则偏导数必连续
D全微分存在,而偏导数不一定存在
正确答案: B解析: 暂无解析 -
第23题:
单选题设z=(x+ey)x,则(∂z/∂x)|(1,0)=( )。A1+2ln2
B2+2ln2
C1+ln2
D2+ln2
正确答案: D解析:
求函数在某一点的偏导数,为了计算简便,可以这样求:
令y=0,则函数z(x,0)=(1+x)x=exln(1+x)。
zx′=exln(1+x)[xln(1+x)]x′=(1+x)x[ln(1+x)+x/(1+x)],zx′(1)=2(ln2+1/2)=1+2ln2,即(∂z/∂x)|(1,0)=1+2ln2。
