在五张卡片的正、反面上分别写有0与1，2与3，4与5，6与7，8与9，将其中任三张并排放在一起组成三位数，共可以组成多少个不同的三位数

题目
在五张卡片的正、反面上分别写有0与1，2与3，4与5，6与7，8与9，将其中任三张并排放在一起组成三位数，共可以组成多少个不同的三位数

相似考题

1.用0到9这10个数字,可以组成________个三位数。A．900B．826C．648D．568

2.如下图所示，X、Y、Z分别是面积为64、180、160的三张不同开关的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为209。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少？A15 B16C14 D18

3.下面程序的功能是统计用0至9之间的不同的数字组成的三位数的个数。main(){ int i,j,k,count=0;for(i=1;i<=9;i++)for(j=0;j<=9;j++)if(【】)continue;else for(k=0;k<=9;k++)if(【】)count++;printf("%d",count);}

4.丙型肝炎在世界上有10个以上基因型,我国以()型为主A、1,2B、3,4C、5,6D、7,8E、9,10

更多“在五张卡片的正、反面上分别写有0与1，2与3，4与5，6与7，8与9，将其中任三张并排放在一起组成三位数，共可以组成多少个不同的三位数”相关问题

  • 第1题：

    有五张卡片。他们的正反面分别写有0与1、2与3、4与5、6与7、8与9，将其中任意三张排放在一起组成三位数，共可组成多少个不同的三位数?

    A．360

    B．242

    C．336

    D．432


    正确答案：D
    先求出组成所有的三位数个数，再减去0在百位的个数。所以，共可组成不同的三位数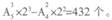

  • 第2题：

    用0，1，2，…，9这10个数字组成一个四位数，一个三位数，一个两位数与一个一位数，每个数字只许用一次，使这四个数的和等于2007，则其中三位数的最小值为（）。

    A. 386 B. 260 C. 230 D. 204


    正确答案：D

    0，1，2，…，9这10个数字之和为45，显然A列数字为1。

    　　D列4个数字之和最小为0+2+3+4=9，最大为9+8+7+6=30，因为D尾数为“7”，则D列4个数字之和为17或27。

    　　假设D列4个数字之和为17时，则C列3个数之和为9或19，对应的B列数字之和为9或8，这四列对应的总和为36和45。所以当D列数字之和为17，C列为19，B列为8，A列为1时，满足条件，这时当A列数字为1;B列数字为2，6;C列为3，7，9;D列为0，4，5，8时三位数取到最小值为230。

    　　假设D列4个数字之和为27时，C列3个数字之和为8或18，对应的B列2个数字之和为9或8，这四列对应数字的总和为45和54。所以当D列数字之和为27，C列为8，B列为9，A列为1时，满足条件。当A列数字为1;B列为2，7;C列为0，3，5;D列为4，6，8，9时，三位数取到最小值为204。可见，其中三位数最小为204。故选D。

  • 第3题：

    方程f(x)=x23-11.1x22+38.8x-41.77=0的有根区间为(9)。

    A．[1,2]

    B．[3,4]

    C．[1,2]、[3,4]

    D．[1,2]、[3,4]、[5,6]


    正确答案：D
    解析：非线性方程f(x)=0求根，包括求超越方程和代数方程的根x*，方程的根也是f(x)的零点，即f(x*)=0，x，可以是实根也可以是复根，本题以求实根为主。求实根首先要确定根x*所在区间[a，b．，称为有根区间。根据连续函数性质，若f(x)在[a，b．上连续，当f(o)f(b)0时，[d，b．为有根区间，为找到方程f(x)=0的有根区间，可用逐次搜索法，也就是在x的不同点上计算fix)，观察f(x)的符号。只要在相邻两点f反号，则得到有根区间，本例得到3个有根区间，分别为[1，2．[3，4．[5，6．。

  • 第4题：

    如图所示，X、Y、Z分别是面积为64、180、160的三张不同形状的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为290。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少?（）[银行真题]

    A.15
    B.16
    C.14
    D.18


    答案：B
    解析：
    根据三个集合的容斥公式，阴影部分的面积为290+24+70+36-(64+180+160)=16。

  • 第5题：

    《棋王》作者把“吃”与“下棋”放在一起写有何用意？


    正确答案: “吃”是物质需要，“下棋”是精神追求，两者构成生命的现实性整体存在，共同塑造出一个具体的王一生。
    在作品发生的苦难时代，“吃”的缺乏与“下棋”一道成为生命的考验，“吃”向人的精神层次的渗透与拓展，是对苦难的超越，对自由的或求，从而与“下棋”获得一致性与同在性。

  • 第6题：

    问答题
    桌子上有3张数字卡片，这几张卡片组成三位数字236。如果把这3张卡片变换一下位置或方向，就会组成另外一个三位数，而且这个三位数恰好能够被47整除。那么如何改变卡片的方位呢？这个三位数是多少呢？

    正确答案： 能够被47整除的三位数有94，141，188，235，282，329……要仔细得观察236这个数字，看怎么变动可以满足要求。可以将236中的23左右交换为32，再把6的那张卡片上下倒置变为“9”即可变为“329”，能够被47整除。
    解析： 暂无解析

  • 第7题：

    有6张卡片，分别写着数字1，2，5，6，8，9。现在从中取出3张卡片，并排放在一起，组成一个三位数。问可以组成多少个不同的偶数?(  )

    A.144个            B.120个             C.60个              D.12个


    C【解析】组成三位数是偶数，则三位数的个位数字只能是偶数。先选最右边的数字，有2，6，8三种不同的选择，即C第二步在其余的5张卡片中任取一张，放在最左边位置上，有5种不同的选择，即C;最后在剩余的4张卡片中任取一张，放在中间的位置上，有4种不同的选择，即C。根据乘法原理，可以组成＝60种

  • 第8题：

    有三张卡片的正反面分别写着1和2，4和6，7和8，用这三张卡片组成三位数，并且6可以当9用，则可得到不同的三位数的个数为：

    A．72

    B．120

    C．144

    D．240


    正确答案：A

  • 第9题：

    将一个三位数的个位数字和百位数字调换后所得的三位数与原三位数的和是1070，差是198，这个三位数是（ ）。

    A. 218
    B. 327
    C. 436
    D. 524

    答案：C
    解析：
    直接代入排除，C项，436 + 634=1070，634-436 = 198，满足条件，答案选C。

  • 第10题：

    小明家的电话号码是7位数。将前四位数组成的数与后三位数组成的数相加得9534，将前三位组成的数与后四位组成的数相加得2523。那么小明家的电话号码是（　　）。
    A.9102322
    B.7801253
    C.8901633
    D.8701453


    答案：C
    解析：
    根据题意设前三位为x，后三位为Y，中间那个数字为a，则10x+a+y=9534，x+1000a+y=2523，解得x=779+111a，y=1744-1111a。因为x、y都为三位数，所以a≠0(a=0，y为四位数)，a=／=2(a=2，Y为负数，x为四位数)，由此可知，当a=1时，x=890，y=633，因此小明家的电话号码为8901633。

  • 第11题：

    如果要将两台计算机通过双绞线以太网直接连接，正确的线序是（）

    • A、1—1，2---2，3---3，4---4，5---5，6----6，7----7，8----8
    • B、1---2，2---1，3---6，4----4，5----5，6----3，7----7，8----8
    • C、1---3，2---6，3----1，4---4，5---5，6---2，7----7，8----8
    • D、1---2，2---1，3---3，4---5，5----4，6---6，7---7，8---8

    正确答案:C

  • 第12题：

    单选题
    用印有“1”“5”“6”的三张卡片，可以组成许多不同的三位数，所有这些三位数的和为（　　）。
    A

    5992

    B

    5993

    C

    5994

    D

    5985


    正确答案： B
    解析：
    印有“6”的卡片即可以当成“6”，也可以当成“9”，所以印有“1”、“5”、“6”的数字能组成的数有156、165、516、561、615、651、159、195、519、591、915、951，利用尾数法可求最后一位，6＋5＋6＋1＋5＋1＋9＋5＋9＋1＋5＋1＝54，则最后一位数为4。

相关内容