一枚均匀硬币连续抛掷3次，求3次均为正面向上的概率．

题目
一枚均匀硬币连续抛掷3次，求3次均为正面向上的概率．

相似考题

1.一枚均匀的硬币连续抛掷3次，求3次均为上面的概率。

2.扔一枚质地均匀的硬币，我们知道出现正面或反面的概率都是0.5，这属于概率应用方法中的( )。A．古典概率方法B．统计概率方法C．主观概率方法D．样本概率方法

3.一枚均匀硬币连续抛掷3次，求3次均在正面向上的概率

4.独立地抛掷一枚质量均匀硬币,已知连续出现了10次反面,问下一次抛掷时出现的是正面的概率是:()A、1/11B、B.1/10C、C.1/2D、D.1/9

更多“一枚均匀硬币连续抛掷3次，求3次均为正面向上的概率．”相关问题

  • 第1题：

    同时抛掷3枚均匀的硬币，则恰好有两枚正面向上的概率为

    A、0.5

    B、0.25

    C、0.125

    D、0.375


    正确答案:D

  • 第2题：

    抛掷一枚硬币，观察其出现正面或反面的过程，就是随机试验，“正面向上”就是随机事件。()


    参考答案：正确

  • 第3题：

    （2）连续4次抛掷一枚硬币，求恰出现两次是正面的概率和最后两次出现是正面的概率。


    正确答案：
              

  • 第4题：

    将3枚均匀的硬币各抛掷一次，恰有2枚正面朝上的概率为 （ ）

    A.A

    B.B

    C.C

    D.D


    正确答案：C
    本题主要考查的知识点为随机事件的概率．【应试指导】

  • 第5题：

    关于频率与概率有下列几种说法
    ①“明天下雨的概率是90％”，表示明天下雨的可能性很大
    ②“抛一枚硬币正面朝上的概率为50％”，表示每抛两次硬币就有一次正面朝上
    ③“某彩票中奖的概率是1％”，表示买10张该种彩票不可能中奖
    ④“抛一枚硬币正面朝上的概率为50％”，表示随着抛掷硬币次数的增加，“抛出正面朝上”这一事件发生的频率稳定在50％附近
    其中正确的说法是()。

    A.①④
    B.②③
    C.④
    D.①③

    答案：A
    解析：
    事件A的概率P(A)是对事件A发生可能性大小的一个度量，它是一个确定的数值，与试

  • 第6题：

    掷一枚均匀的硬币若干次，当正面向上次数大于反面向上次数时停止，则在4次之内停止的概率为



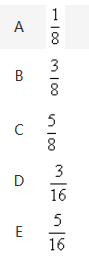    答案：C
    解析：

  • 第7题：

    同时抛掷三枚均匀的硬币，正面与反面都出现的概率为( )。

    A、1/4
    B、1/3
    C、2/3
    D、3/4

    答案：D
    解析：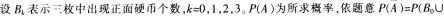

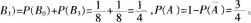
  • 第8题：

    假设扔一枚质地均匀的硬币，我们知道出现正面或反面的概率都是0.5，这属于概率应用方法中的()。

    A:古典概率方法
    B:先验概率方法
    C:主观概率方法
    D:样本概率方法
    E:统计概率方法

    答案：A,B
    解析：
    可用古典概率或先验概率方法进行计算的随机现象应同时具有以下特征：①在试验中它的全部可能结果是有限的，并且这些事件是两两互不相容的；②各事件的发生或出现是等可能的。本题中，扔硬币出现的可能结果的范围仅限于正面或反面，并且结果的出现具有等可能性。

  • 第9题：

    抛掷一枚硬币，正面朝上还是反面朝上，这一现象符合正态分布。


    正确答案:错误

  • 第10题：

    抛掷一枚均匀的硬币，出现正面的概率是（）。

    • A、0
    • B、1
    • C、0.5
    • D、0.8

    正确答案:C

  • 第11题：

    同时掷3枚均匀硬币，则至多有1枚硬币正面向上的概率为（）

    • A、1/8
    • B、1/6
    • C、1/4
    • D、1/2

    正确答案:D

  • 第12题：

    判断题
    抛一个质量均匀的硬币，其正面向上的概率为1/2，因此在抛这个硬币100次时，不可能出现没有正面向上的情况。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第13题：

    同时掷3枚均匀硬币,恰好有2枚正面向上的概率为( )。

    A.0.5

    B.0.25

    C.0.125

    D.0.375


    参考答案：D

  • 第14题：

    将一枚匀称的硬币连续掷两次，则正面只出现一次的概率为()

    A、1/3

    B、0.5

    C、0.6

    D、0.1


    参考答案：B


  • 第15题：

    根据概率论，抛掷一枚均匀的硬币，其正面朝上和反面朝上的概率几乎相等。我与人打赌，若抛掷硬币正面朝上，我赢；若反面朝上，我输。我抛掷硬币6次，结果都是反面朝上，已经连输了6次。因此，我后面的几次抛掷肯定是正面朝上，一定会赢回来。

    下面哪一个选项是对“我”的推理的恰当评价？

    A．有道理，因为上帝是公平的，几乎是均等的，他不回总倒霉。

    B．没道理，因为每一次抛掷都是独立事件，与前面的结果没有关系。

    C．后面几次抛掷果然大多正面朝上，这表明概率论是正确的。

    D．这只是他个人的信念，无法进行理性的或逻辑的评价。


    正确答案：B

  • 第16题：

    通常认为，抛掷一枚质量均匀的硬币的结果是随机的。但实际上，抛掷结果是由抛掷硬币的冲力和初始高度共同决定的。尽管如此，对抛掷硬币的结果作出准确预测还是十分困难。下面哪一项最有助于解释题干所说的现象，即抛掷结果被某些因素决定，但预测却很困难?

    A．很长时间以来，抛掷硬币已被用作随机事件的典型例证。

    B．如果抛掷一枚质量不均匀的硬币，其结果总能被精确地预测。

    C．如果抛掷硬币的初始高度保持稳定不变，则抛掷硬币的结果将仅由抛掷冲力决定。

    D．对抛掷硬币结果的准确预测，要求极其精确地估计抛掷硬币的初始高度和冲力。


    正确答案：D
    解析：题干的结论是：虽然可以确定抛掷结果是由哪些因素决定，但预测结果还是很困难。要解释这个结论必须说明，决定结果的因素很难精确估计，即选项D。

  • 第17题：

    在抛一枚质量均匀的硬币的实验中，统计出正面向上的次数占实验总次数的50.33％，这里的50.33％叫做“正面向上”这个事件发生的______，在大量的重复实验中发现它在0.5左右摆动，这个0.5叫做“正面向上”这个事件发生的______。


    答案：
    解析：
    频率，概率。解析：事件发生总次数与实验总次数的比值，称为这个事件的频率；随机事件的频率总在某个常数附近摆动，且随着试验次数不断增多，摆动幅度越来越小，这个常数称为随机事件的概率。

  • 第18题：

    扔一枚质地均匀的硬币，我们知道出现正面或反面的概率都是0.5，这属于概率应用方法中的()。

    A:古典概率方法
    B:统计概率方法
    C:主观概率方法
    D:样本概率方法

    答案：A
    解析：

  • 第19题：

    同时抛掷 3 枚均匀的硬币，恰好有两枚正面向上的概率为（ ）。

    A.1/4
    B.3/8
    C.1/2
    D.1/3

    答案：B
    解析：
    每枚硬币都有正反两面，三枚硬币共有8种情况，两枚正面向上的情况有：正正反、正反正、反正正,3种。

  • 第20题：

    连抛一枚均匀硬币4次，既有正面又有反面的概率为（ ）。
    A. 1/16 B. 1/8 C. 5/8 D. 7/8


    答案：D
    解析：
    连抛硬币4次可重复排列数为：n=24= 16。而全是正面或全是反面各1种可能，所以既有正面又有反面的有：k = 16－2 =14种可能。故“既有正面又有反面”的概率为：P（A） =k/n=7/8。

  • 第21题：

    晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为。（）

    • A、1/2
    • B、1/11
    • C、1/7
    • D、1/18。

    正确答案:A

  • 第22题：

    抛掷一个硬币，有时会正面向上，有时会反面向上，这说明了抛掷硬币这个事件具有某种：（）

    • A、随机性
    • B、不可预见性
    • C、确定性
    • D、规律性

    正确答案:A

  • 第23题：

    抛一个质量均匀的硬币，其正面向上的概率为1/2，因此在抛这个硬币100次时，不可能出现没有正面向上的情况。


    正确答案:错误

相关内容