求函数(x)=x3-3x+1的单调区间和极值．

题目
求函数(x)=x3-3x+1的单调区间和极值．

相似考题

1.设f(x)=xe-x，求函数f(x)的极值（6分）

2.(本题满分8分)求函数y＝x3-3x2-1的单调区间、极值及其曲线的凹凸区间和拐点。

3.设函数f（x）=x4-4x+5．（I）求f（x）的单调区间，并说明它在各区间的单调性；（Ⅱ）求f（x）在区间[0，2]的最大值与最小值．

4.求函数y=x-ln(1+x)的极值.

更多“求函数(x)=x3-3x+1的单调区间和极值．”相关问题

  • 第1题：

    已知函数f（x）=x3 +ax2+b，曲线y=f（x）在点（1，1）处的切线为y=x．

    （I）求a，b；

    （II）求f（x）的单调区间，并说明它在各区间的单调性．


    正确答案：

  • 第2题：

    设函数f(x，y)=X2+Y2+xy+3，求f(x，y)的极值点与极值．


    答案：
    解析：

  • 第3题：

    求函数z=x2+y2+2y的极值．


    答案：
    解析：

  • 第4题：

    求函数(x)=x3-3x-2的单调区间和极值．


    答案：
    解析：
    函数的定义域为(-∞，+∞)．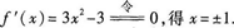
    列表如下：

    函数(x)的单调增区间为(-∞，-1)，(1，+∞)；单调减区间为(-1，1)．极大值为(-1)=0，极小值为(1)=-4．

  • 第5题：

    求函数(x，y)=4(x-y)-x2-y2的极值．


    答案：
    解析：

    所以(2，-2)=8为极大值．

  • 第6题：

    设z=z(x,y)是由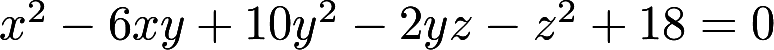 确定的函数，求 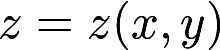的极值点和极值


    答案：
    解析：

  • 第7题：

    下列命题中，正确的是( ).

    A.单调函数的导函数必定为单调函数
    B.设f´(x)为单调函数，则f(x)也为单调函数
    C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
    D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

    答案：D
    解析：
    可导函数的极值点必定是函数的驻点，故选D.

  • 第8题：

    设函数(x)=2x3+3mx2-36x+m，且′(-1)=-36．
    (Ⅰ)求m；
    (Ⅱ)求(x)的单调区间．


    答案：
    解析：

    当x>2时，′(x)>0．
    故(x)的单调递减区间为(-3，2)，(x)的单调递增区间为(-∞，-3)，(2，+∞)．

  • 第9题：

    求函数f(x，y)=e2x(x+y2+2y)的极值.?


    答案：
    解析：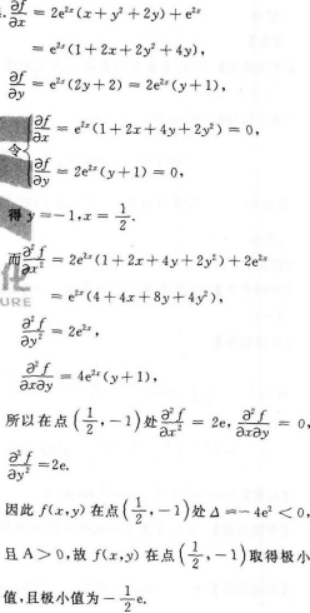

  • 第10题：

    求函数f(x)=x3-3x+1的单调区间和极值．


    答案：
    解析：
    函数的定义域为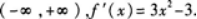




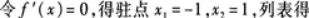
    注意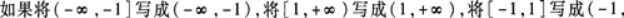

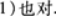
    【评析】判定f(x)的极值，如果x0为f（x)的驻点或不可导的点，可以考虑利用极值的第一充分条件判定．但是当驻点处二阶导数易求时，可以考虑利用极值的第二充分条件判定．

  • 第11题：

    求函数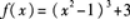的单调区间和极值．


    答案：
    解析：
    函数的定义域为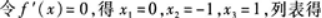

    函数f(x)的单调减区间为(-∞，0]，函数f(x)的单调增区间为[0，+∞)；f(0)=2为极小值．

  • 第12题：



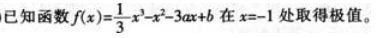
    (1)求实数a的值；
    (2)求函数 (x)的单调区间。


    答案：
    解析：

  • 第13题：

    确定函数y=2x4-12x2的单调区间、极值及函数曲线的凸凹性区间和拐点．


    答案：
    解析：

  • 第14题：

    求y=f(x)=2x3-3x2-12x+14的极值点和极值，以及函数曲线的凸凹性区间和拐点.


    答案：
    解析：
    y'=6x2-6x-12，y''=12x-6，令y'=0得驻点x1=-1,x2=2，当x2=2时，y''=18>0．所以f(z)在x=2处取极小值-6．当x1=-1时，y''<0．所以f(x)在x=-1处取极大值21．

  • 第15题：

    求函数(x)=x3-3x2-9x+2的单调区间和极值．


    答案：
    解析：
    (x)的定义域为(-∞，+∞)．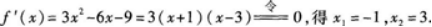
    列表如下：

    函数发(x)的单调增加区间为(-∞，-l)，(3，+∞)；单调减少区间为(-1，3)．极大值发(-1)=7，极小值(3)=-25．

  • 第16题：

    已知函数(x)=x4-4x+1．
    (1)求(x)的单调区间和极值；
    (2)求曲线y=(x)的凹凸区间．


    答案：
    解析：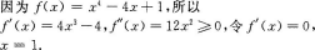

    列表如下，



    由表可知曲线(x)的单调递减区间为(-∞，1)，单调递增区间为(1，+∞)．由于"(x)=12x2≥0，所以为凹曲线，凹区间为(-∞，+∞)，极小值为(1)=1-4+1=-2．

  • 第17题：

    已知函数f(x)=（1/2）e2x-ax，g(x)=6xlnx，，h(x)=2e2x-4/x，a>o，b≠0。
    (1)求函数f(x)的最小值；(3分)
    (2)求函数g(x)的单调区间；(3分)
    (3)证明：函数h(x)在[1/2，1]上有且仅有l个零点。(4分)


    答案：
    解析：

  • 第18题：

    求函数的单调区间与极值.


    答案：
    解析：
    函数f(x)的定义域为(-∞，+∞)，且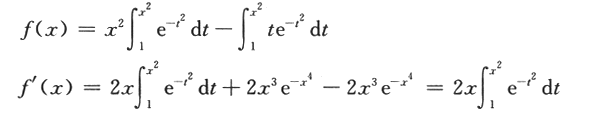

    令f'(x)=0，得x=0,x=±1，列表如下：

    由以上表格可知，f(x)单调增加区间为(-1，0)和(0，+∞)；f(x)单调减少的区间为(-∞，-1)和(0，1).f(x)的极小值为

    【评注】本题主要考查变上限积分求导和定积分计算，以及求函数单调在区间与极值的方法.考的是基本内容和常见问题，但该题的得分率并不高，考生的主要问题是
    1)不能正确求出是最普通的错误；
    2)部分考生由于粗心只求出一个驻点x=0，漏掉了驻点x=±1；
    3)部分考生不能正确表示单调区间，将单调增加区间写成了(-1，0)∪(1，+∞)，单调减少区间写成了(-∞，-1)∪(0，1).

  • 第19题：

    设函数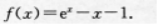
    (I)求f(χ)的单调区间；
    (Ⅱ)求f(χ)的极值．


    答案：
    解析：

  • 第20题：

    （本小题13分）已知函数f(x)=2x3-3x2，求
    （1）函数的单调区间；
    （2）函数f(x)在区间[-3,2]的最大值与最小值。


    答案：
    解析：

  • 第21题：

    求函数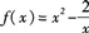一的单调区间、极值及其曲线的凹凸区间和拐点．


    答案：
    解析：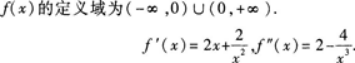


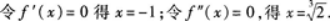
    列表：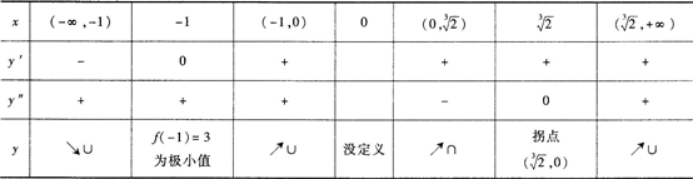


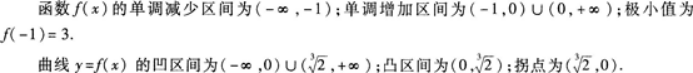
    说明


    【评析】拐点(x0fx0))的坐标如果写成单一值x0或写为单一值fx0)都是错误的．

  • 第22题：

    求函数y=x-lnx的单调区间，并求该曲线在点(1，1)处的切线l的方程．


    答案：
    解析：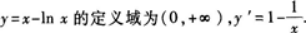


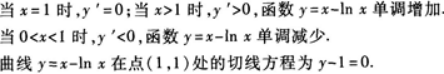
    【评析】求函数f(x)的单调区间，应先判定函数的定义域．求出函数的驻点，即y′=0的点；求出y的不可导的点，再找出y′>0时x的取值范围，这个范围可能是一个区间，也可能为几个区间．

  • 第23题：

    已知函数



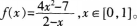
    (1)求f(x)单调区间与值域；
    (2)设a≥1，函数g(x)=x3-3a2x-2a，x∈[0，1]。若对于任意x1∈[0，1]，总存在x0∈[0，1]使g(x0)=f(x1)成立，求a的取值范围。



    答案：
    解析：

相关内容