求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分．

题目

相似考题

1.求微分方程ex-ydx-dy=0的通解.

2.(本题满分8分) 设函数z=z(x，y)是由方程x+y3+z+e2x=1所确定的隐函数，求dz．

3.微分方程ydx+(y2x-ey)dy=0是( )方程。 A.可分离变量 B.一阶线性的微分 C.全微分 D.齐次

4.设函数y=y(x)由方程y+arcsinx=ex+y确定。求dy.

更多“求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分．”相关问题

第1题：

微分方程：ydx+（y2x-ey）dy=0是下述哪种方程？

A.可分离变量方程
B.—阶线性的微分方程
C.全微分方程
D.齐次方程

答案：B
解析：
提示：方程可化为x'+p（y）x=Q（y）的形式。
第2题：

求下列函数的全微分

答案：
解析：
第3题：

求方程所确定的隐函数的导数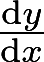

答案：
解析：
第4题：

设非负函数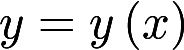满足微分方程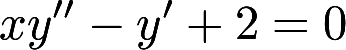，当曲线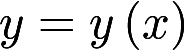过原点时，其与直线x=1及y=0围成平面区域D的面积为2，求D绕y轴旋转所得旋转体的体积

答案：
解析：
第5题：

设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.

答案：
解析：
第6题：

已知微分方程y’+y=f(x)，其中f(x)是R上的连续函数.
　　(Ⅰ)若f(x)=x，求方程的通解.
　　(Ⅱ)若f(x)是周期为T的函数，证明：方程存在唯一的以T为周期的解.

答案：
解析：
【解】(Ⅰ)若f(x)=x，则方程为y'+y=x通解为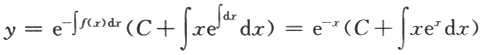

(Ⅱ)设y(x)为方程的任意解，则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T，有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0，有(e^x［y(x+T)-y(x)］)'=0，
即e^x［y(x+T)=y(x)］=C.取C=0得y(x+T)-y(x)=0，
y(x)为唯一以T为周期的解.
第7题：

设F(χ)=f(χ)g(χ)，其中函数f(χ)，g(χ)在(-∞，+∞)内满足以下条件： f’(χ)=g(χ)，g’(χ)=f(χ)，且f(0)=0，f(χ)+g(χ)=2eχ。 (1)求F(χ)所满足的一阶微分方程； (2)求出F(χ)的表达式。

答案：
解析：
第8题：

求微分方程的通解．

答案：
解析：
第9题：

在微分方程中出现的未知函数的最高阶导函数的阶数被称为微分方程的阶。

正确答案:正确
第10题：

拉氏变换求解微分方程步骤包括：（1）考虑初始条件，对微分方程进行（）；（2）求出输出变量的拉氏变换表达式；（3）对输出变量拉氏变换函数求（），得到输出变量的时域表达式。

正确答案:拉氏变换；反变换
第11题：

单选题
由x2－xy＋y2＝C确定的隐函数满足的微分方程是（　　）。
A
（x－2y）y′＝2x－y
B
（x－2y）y′＝2x
C
xy′＝2x－y
D
－2yy′＝2x－y

正确答案： C
解析：
由x²－xy＋y²＝C，两边对x求导得2x－y－xy′＋2yy′＝0，整理得（x－2y）y′＝2x－y。
第12题：

问答题
设微分方程由通解y＝（C1＋C2x＋x－1）e－x，求此微分方程。

正确答案：
已知y=(C₁+C₂x+x^-¹)e^-^x,求导得
y′=-(C₁+C₂x+x^-¹)e^-^x+(C₂-x^-²)e^-^x=-y+(C₂-x^-²)e^-^x,
y″=-y′+2x^-³e^-^x-(C₂-x^-²)e^-^x=-y′+2x^-³e^-^x-y′-y=-2y′+2x^-³e^-^x-y,整理后可得到所求微分方程y″+2y′+y=2x^-³e^-^x=2e^-^x/x³。
解析：暂无解析
第13题：

求由方程2x2+y2+z2+2xy-2x-2y-4x+4=0确定的隐函数的全微分．

答案：
解析：
所以dz=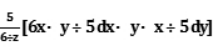
第14题：

设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．

答案：
解析：
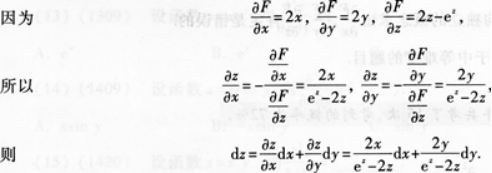
第15题：

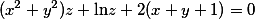已知函数由方程确定求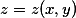的极值

答案：
解析：
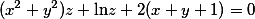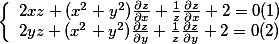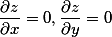由,两边分别同时对x，y求偏导数得：令(3) 得:(4)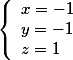
第16题：

已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定，求y(x)的极值.

答案：
解析：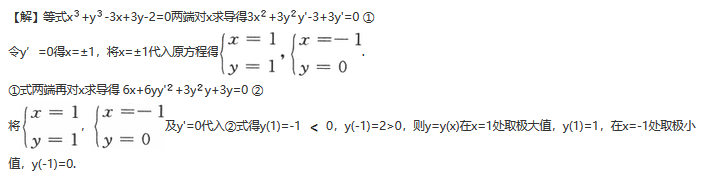
第17题：

设函数y(x)是微分方程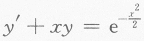满足条件y(0)=0的特解.
　　(Ⅰ)求y(x)；
　　(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.

答案：
解析：
第18题：

关于同步发电机机端三相短路的分析，下述说法中正确的是（）。

A.派克变换的目的是将描述发电机电磁暂态过程的原始电压方程由变系数微分方程变为常系数微分方程
B.将派克变换后的同步发电机基本方程进行拉普拉斯变换的目的是将基本方程由微分方程变为代数方程
C.对同步发电机机端三相短路进行定量分析的基本方法是，利用象函数表示的发电机基本方程和边界条件，求出待求量的象函数，再进行拉普拉斯变换求待求量的原函数（d、q、0等效绕组系统中的电气量）
D.派克变换仅适用于同步发电机三相对称短路的分析计算

答案：A,B,C
解析：
派克变换的目的是将描述发电机电磁暂态过程的原始电压方程由变系数微分方程变为常系数微分方程；将派克变换后的同步发电机基本方程进行拉普拉斯变换的目的是将基本方程由微分方程变为代数方程；对同步发电机机端三相短路进行定量分析的基本方法是，利用象函数表示的发电机基本方程和边界条件，求出待求量的象函数，再进行拉普拉斯变换求待求量的原函数（d、q、0等效绕组系统中的电气量）。
第19题：

设Z=Z(x，Y)是由方程x+y3+z+e2=1确定的函数，求dz

答案：
解析：
利用隐函数求偏导数公式，记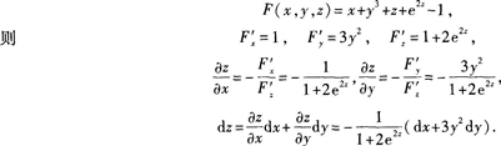
第20题：

微分方程ydx+（y²x-e^y）dy=0是下述哪种方程（）？
- A、可分离变量方程
- B、一阶线性的微分方程
- C、全微分方程
- D、齐次方程
正确答案:B
第21题：

关于同步发电机机端三相短路的分析，下述说法中错误的是：（）。
- A、派克变换的目的是为了将描述发电机电磁暂态过程的原始电压方程由变系数微分方程变为常系数微分方程
- B、将派克变换后的同步发电机基本方程进行拉普拉斯变换的目的是将基本方程由微分方程变为代数方程
- C、对同步发电机机端三相短路进行定量分析的基本方法是，利用用象函数表示的发电机基本方程和边界条件，求出待求量的象函数，再进行拉普拉斯反变换求待求量的原函数（d、q、0等效绕组系统中的电气量），最后通过派克变换求出定子三相绕组系统中的电气量
- D、派克变换仅适用于同步发电机三相对称短路的分析计算
正确答案:D
第22题：

问答题
求由方程x2＋y2＋z2－xz－yz－2x－2y＋2z－6＝0确定的函数z＝z（x，y）的极值。

正确答案：
先求出函数z的各个偏导:
由原方程可得,原方程两边对x求导得
2x+2z·z_x′-z-(x+y)z_x′-2+2z_x′=0①
原方程两边对y求导得
2y+2z·z_y′-z-(x+y)z_y′-2+2z_y′=0②
①②中,令z_x′=0,z_y′=0,解得x=(z+2)/2,y=(z+2)/2,将其代入已知方程得Z=±4,故驻点为(3,3)和(-1,-1)。
①式两边对x,y分别求导得
2+2(z_x′)²+2zz_xx″-2z_x′+(2-x-y)z_xx″=0③
2z_y′z_x′+2zz_xy″-z_y′-z_x′+(2-x-y)z_xy″=0④
②式两边对y求导得
2+2(z_y′)²+2zz_yy″-2z_y′+(2-x-y)z_yy″=0⑤
当x=y=-1,z=-4时,z_x′=z_y′=0,将其代入③④⑤,得A=z_xx″(-1,-1)=1/2,B=z_xy″(-1,-1)=0,C=z_yy″(-1,-1)=1/2,B²-AC=-1/4<0,A=1/2>0。
则函数z在(-1,-1)处取得极小值z=-4。
当x=y=3,z=4时,z_x′=z_y′=0,并将其代入③④⑤,得A=z_xx″(3,3)=-1/2,B=z_xy″(3,3)=0,C=z_yy″(3,3)=-1/2,B²-AC=-1/4<0,A=-1/2<0。
故z在(3,3)点处取到极大值z=4。
解析：暂无解析
第23题：

单选题
微分方程ydx+（y2x-ey）dy=0是下述哪种方程（）？
A
可分离变量方程
B
一阶线性的微分方程
C
全微分方程
D
齐次方程

正确答案： B
解析：方程可化为x′+P（y）x=Q（y）的形式。

求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分．

题目

相似考题

更多“求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分．”相关问题

相关内容