某项目从现在开始投资，2年内没有回报，从第3年开始每年年末获利额为10万元，获利年限为5年，则该项目利润的现值为( )。A．10×(P/A，i，5)×(P/F，i，2)B．10×[(P/A，i，7)-(P/A，i，2)]C．10×[(P/A，i，7)-(P/A，i，3)]D．10×(P/A，i，5)×(P/F，i，3)

题目

某项目从现在开始投资，2年内没有回报，从第3年开始每年年末获利额为10万元，获利年限为5年，则该项目利润的现值为( )。

A．10×(P/A，i，5)×(P/F，i，2)

B．10×[(P/A，i，7)-(P/A，i，2)]

C．10×[(P/A，i，7)-(P/A，i，3)]

D．10×(P/A，i，5)×(P/F，i，3)

相似考题

1.某项目从现在开始投资，2年内没有回报，从第3年开始每年获利额为 10万元，获利年限为5年，则该项目利润的现值为( )。A．10×(P/A，i，5)×(P/F，i，2)B．10×[(P/A，i，7)-10×(P/A，i，2)]C．10×[(p/A，i，7)-10×(p/A，i，3)]D．10×(P/A，i，5)×(P/F，i，3)

2.某项目从现在开始投资，2年内没有回报，从第3年开始每年获利额为A，获利年限为5年，则该项目利润的现值为（ ）。A．A×（P/A，i，5）×（P/F，i，3）B．A×（P/A，i，5）×（P/F，i，2）C．A×（P/A，i，7）-A×（P/A，i，2）D．A×（P/A，i，7）-A×（P/A，i，3）

3.有以下程序 struct S{ int n；int a[20]；}； voidf(struct S*p) { int i，j，t； for(i=0；i＜p-＞n-1；i++) for(j=i+1；j＜p-＞n；j++) if(p-＞a[i]＞p-＞a[j]){t=p-＞a[i]；p-＞a[i]=p-＞a[j]；p-＞a[j]=t;} } main() { int i；struct S s={10，{2，3，l，6，8，7，5，4，10，9}}； f(&s)； for(i=0；i＜s.n；i++)printf("%d，"，s.a[i])； } 程序运行后的输出结果是A．1，2，3，4，5，6，7，8，9，10，B．10，9，8，7，6，5，4，3，2，1，C．2，3，1，6，8，7，5，4，10，9，D．10，9，8，7，6，1，2，3，4，5，

4.有以下程序struct S {int n; int a[20];}; void f（struct S *P） {int i,j,t; for（i=0;in-1;i++） for（j=i+1;jn;j++） if（p->a[i]>p->a[j]） { t=p->a[i]; p->a[i]=p->a[j]; p->a[j]=t; } } main（） {int i; struct S s={10,{2,3,1,6,8,7,5,4,10,9}}; f（&s）; for（i=0;i printf（“%d”,s.a[i]）; } 程序运行后的输出结果是（ ）。 A．1,2,3,4,5,6,7,8,9,10,B．10,9,8,7,6,5,4,3,2,1,C．2,3,1,6,8,7,5,4,10,9,D．10,9,8,7,6,1,2,3,4,5,

更多“某项目从现在开始投资，2年内没有回报，从第3年开始每年年末获利额为10万元，获利年限为5年，则该项目利润的现值为( )。A．10×(P/A，i，5)×(P/F，i，2)B．10×[(P/A，i，7)-(P/A，i，2)]C．10×[(P/A，i，7)-(P/A，i，3)]D．10×(P/A，i，5)×(P/F，i，3)”相关问题

  • 第1题：

    某项目从现在开始投资，2年内没有回报，从第3开始每年获利额为A，获利年限为5年，则该项目利润的现值为( )。

    Ⅰ．A×(P/A，i，5)×(P/S，i，3)

    Ⅱ．A×(P/A，i，5)×(P/S，i，2)

    Ⅲ．A×(P/A，i，7)-A×(P/A，i，2)

    Ⅳ．A×(P/A，i，7)-A×(P/A，i，3)

    Ⅴ．Ⅰ、Ⅲ

    A．Ⅱ、Ⅳ

    B．Ⅰ、Ⅳ

    C．Ⅱ、Ⅲ


    参考答案：C
    解析：递延年金现值=A×(P/A，i，n-s)×(P/S，i，n)=A×[(P/A，i，n)-(P/A，i，s)]，其中s表示递延期n表示总期数。可见，Ⅱ、Ⅲ两项符合题意。

  • 第2题：

    从第4年开始每年年初有现金流入1000元，连续流入8笔，则下列计算其现值的表达式中正确的有（）。

    A.P＝1000×（P/A，i，8）×（P/F，i，2）
    B.P＝1000×[（P/A，i，7）＋1]×（P/F，i，3）
    C.P＝1000×（F/A，i，8）×（P/F，i，10）
    D.P＝1000×［（P/A，i，10）－（P/A，i，2）］

    答案：A,B,C,D
    解析：
    从第4年开始每年年初有现金流入1000元，连续流入8笔，相当于从第3年开始每年年末有现金流入1000元，连续流入8笔。因此，递延期m＝2，年金个数n＝8，

  • 第3题：

    一人准备在今后7年每年年末存入A元，利率为I，则第8年年末可以得到F的正确表达式是（ ）。

    A：F=A（P/A,I,7）（F/P,I,8）
    B：F=A（P/A,I,6）（F/P,I,7）
    C：F=A（F/A,I,7）（F/P,I,1）
    D：F=A（F/A,I,6）（F/P,I,2）
    E：F=A（F/A，I，7）

    答案：A,C
    解析：
    2019版教材P163
    本题考查的是等值计算。选项A首先计算到第0年，然后再用现值终值公式计算到第8年；选项C先计算到第7年，然后再用现值终值公式计算到第8年。

  • 第4题：

    在下列现金流量图中，已知A、F和i，则P=（　）。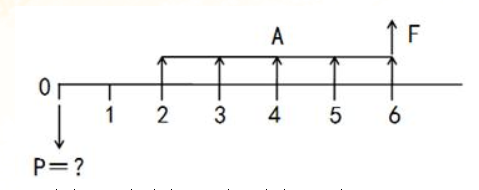


    A、A（P/A，i，5）（P/F，i，1）+F（P/F，i，6）
    B、A（P/A，i，6）+F（P/F，i，6）
    C、A（P/A，i，5）+F（P/F，i，6）
    D、A（P/A，i，5）（P/F，i，2）+F（P/F，i，6）

    答案：A
    解析：
    本题考查的是复利计算。A（P/A，i，5）计算得到第一期期末的现值，然后通过终值折算为现值公式将第一年年末的值折算到期初，即为：A（P/A，i，5）（P/F，i，1）；最后套用已知终值求现值公式将第六期期末的终值折算到期初。参见教材P158～159。

  • 第5题：

    根据资金时间价值的原理，在年利率为i情况下，将发生在第2、3、4、5年年末的等额年金80万元折算到第1年年初的现值，其金额为( )万元。

    A.80(P/A，i，4)
    B.80(P/A，i，4)(P/F，i，1)
    C.80(P/F，i，4)
    D.80(P/F，i，4)(P/F，i，1)

    答案：B
    解析：

  • 第6题：

    某公司准备在今后7年每年年末存入A元，利率为I，则第8年年末可以得到F的正确表达式是（）。

    A.F=A(P／A，I，7)(F／P，I，8)
    B.F=A(P／A，I，6)(F／P，I，7)
    C.F=A(F／A，I，7)(F／P，I，1)
    D.F=A(F／A，I，6)(F／P，I，2)
    E.F=A(F／A，I，7)

    答案：A,C
    解析：
    2020教材P68-75
    选项A，首先将各年的A折现到期初，然后再用现值终值公式计算到第8年；选项C，先将各年的A计算到第7年末，然后再用现值终值公式计算到第8年。

  • 第7题：

    一人准备在今后7年每年年末存入A元，利率为I，则第8年年末可以得到F的正确表达式有（ ）。

    A.F=A(P／A，I，7)(F／P，I，8)
    B.F=A(F／P，I，6)(F／P，I，7)
    C.F=A(F／A，I，7)(F／P，I，1)
    D.F=A(F／A，I，6)(F／P，I，2)
    E.F=A(F／A，I，7)

    答案：A,C
    解析：
    本题考查的是等值计算。选项A：首先已知A求2020教材P，计算到第0年，然后再用现值终值公式计算到第8年；选项C先计算到第7年，然后再用现值终值公式计算到第8年。2020教材P162-175

  • 第8题：

    某项目从现在开始投资，2年内没有回报，从第3年开始每年获利额为4，获利年限为5年，则该项目利润的现值为()。①A*（P/A，i，5）*(P/S,i，3)②A*(P/A，i，5）*(P/S,i，2)③A*（P/A，i，7）-A*（P/A，i，2）④A*（P/A，i，7）-A*（P/A，i，3）

    A:①③
    B:①④
    C:②③
    D:②④

    答案：C
    解析：
    递延年金现值=A*（P/A，i，n-s）*(P/S,i，s)=A*[（P/A，i，n）-(P/A，i，s)]，其中s表示递延期，n表示总期数。

  • 第9题：

    已知n=n1+n2，则（）。

    • A、（F／P，i，n）=（F／P，i，n1）+（F／P，i，n2）
    • B、（F／P，i，n）=（F／P，i，n1）×（F／P，i，n2）
    • C、（P／F，i，n）=（P／F，i，n1）+（P／F，i，n2）
    • D、（P／F，i，n）=（P／F，i，n1）×（F／P，i，n2）

    正确答案:B

  • 第10题：

    单选题
    若P位于第一年末，F位于第n年初，复利利率为i，则P的表达式是（）
    A

    P=F（P/F，i，n）（F/P，i，1）

    B

    P=F（P/F，I，n）

    C

    P=F（P/F，I，n-2）

    D

    P=F（P/F，I，n-1）（F/P，I，2）


    正确答案： A
    解析： 暂无解析

  • 第11题：

    多选题
    某公司准备在今后7年每年年末存入A元，利率为I，则第8年年末可以得到F的正确表达式是( )。
    A

    F=A (P/A,I,7)(F/P,I,8)

    B

    F=A (P/A,I,6)(F/P,I,7)

    C

    F=A (F/A,I,7)(F/P,I,1)

    D

    F=A (F/A,I，6)(F/P,I,2)

    E

    F=A (F/A，I，7)


    正确答案： E,D
    解析：

  • 第12题：

    多选题
    已知现金流量如下图所示，计算F的正确表达式是（）。
    A

    F＝A（P／A，i，6）（F／P，i，8）

    B

    F＝A（P／A，i，5）（F／P，i，7）

    C

    F＝A（P／A，i，6）（F／P，i，2）

    D

    F＝A（P／A，i，5）（F／P，i，2）

    E

    F＝A（P／A，i，6）（F／P，i，1）


    正确答案： B,A
    解析： 暂无解析

  • 第13题：

    某项目的现金流量如下图所示，则下列等是正确的有（　）。
    【图
    A、P=-30（P/A，i，3）+40（P/F，i，4）+60（P/A，i，5）（P/F，i，5）
    B、P=-30（P/A，i，4）（1+i）+40（P/F，i，4）+60（P/A，i，6）（P/F，i，4）
    C、P=-30-30（P/A，i，3）+40（P/F，i，4）+60（P/A，i，10）
    D、P=-30-30（P/A，i，3）+40（P/F，i，4）+60（P/A，i，5）（P/F，i，5）
    E、P=-30-30（P/A，i，3）+40（P/F，i，4）+60（P/A，i，6）（P/F，i，4）】


    答案：B,E
    解析：
    本题考查的是等值计算。年金折现一定要折到第一笔年金的前一年。比如本题中，0-3年的等额支出折现时只能折到0的前一年，而现值是在0那点的价值，因此可以有两种处理方法：一种是先整体折到-1年，再往0点折算，比如答案B；另一种处理方法是，将这笔等额支出分成两部分，在0点的不需折现，1-3年的再按年金现值折算，比如答案E；另一个问题是关于公式中n的确定，如果年金数量较少，可以数年金个数，即为n；当年金数量较多时，用最后一笔年金发生的时点减去第一笔年金的前一年，即为n。如本题中5-10年的年金60，折现时需先折算到第5年初（4年末），则年金个数为10-4=6，然后再从第4年末一次折现到0点。参见教材P159。

  • 第14题：

    有一项年金，前2年无流入，后6年每年初流入100元，则下列计算其现值的表达式正确的有（　）。

    A.P＝100×（P/A，i，6）（P/F，i，2）
    B.P＝100×（P/A，i，6）（P/F，i，1）
    C.P＝100×（F/A，i，6）（P/F，i，7）
    D.P＝100×［（P/A，i，7）－（P/F，i，1）］

    答案：B,C,D
    解析：
    “前2年无流入，后6年每年初流入100元”意味着从第3年开始每年年初有现金流入100元，共6笔，也就是从第2年开始每年年末有现金流入100元，共6笔。因此，递延期m＝1，年金个数n＝6。所以选项B、C正确。因为（P/F，i，1）＝（P/A，i，1），所以选项D也正确。

  • 第15题：

    (2017年真题) 在下列现金流量图中，已知A、F和i，则P=（）。


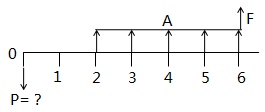    A.A（P/A，i，5）（P/F，i，1）+F（P/F，i，6）
    B.A（P/A，i，6）+F（P/F，i，6）
    C.A（P/A，i，5）+F（P/F，i，6）
    D.A（P/A，i，5）（P/F，i，2）+F（P/F，i，6）

    答案：A
    解析：
    本题考查的是复利计算。A（P/A，i，5）计算得到第一期期末的现值，然后通过终值折算为现值公式将第一年年末的值折算到期初，即为：A（P/A，i，5）（P/F，i，1）；最后套用已知终值求现值公式将第六期期末的终值折算到期初。

  • 第16题：


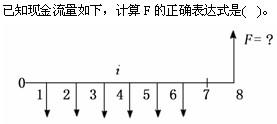    A.F=A(P/A，i，6)(F/P，i，8)
    B.F=A(P/A，i，5)(F/P，i，7)
    C.F=A(F/A，i，6)(F/P，i，2)
    D.F=A(F/A，i，5)(F/P，i，2)
    E.F=A(F/A，i，6)(F/P，i，l)

    答案：A,C
    解析：

  • 第17题：

    已知现金流量如下图所示，计算F的正确表达式是( )。

    A:F=A(P/A,i,6)(F/P,i,8)
    B:F=A(P/A,i,5)(F/P,i,7)
    C:F=A(P/A,i,6)(F/P,i,2)
    D:F=A(P/A,i,5)(F/P,i,2)
    E:F=A(P/A,i,6)(F/P,i,1)

    答案：A,C
    解析：

  • 第18题：

    某项目的现金流量如下图所示，则下列等式正确的有（ ）。

    A.P=-30(P／A，i，3)+40(P／F，i，4)+60(P／A，i，5)(P／F，i，5)
    B.P=-30(P／A，i，4)（1+i）+40(P／F，i，4)+60(P／A，i，6)(P／F，i，4)
    C.P=-30-30(P／A，i，3)+40(P／F，i，4)+60(P／A，i，10)
    D.P=-30-30(P／A，i，3)+40(P／F，i，4)+60(P／A，i，5)(P／F，i，5)
    E.P=-30-30(P／A，i，3)+40(P／F，i，4)+60(P／A，i，6)(P／F，i，4)

    答案：B,E
    解析：
    本题考查的是等值计算。本题关键是关于年金折算的问题，一个是关于年金折算点的确定，一个是关于折现公式中n的确定。年金折现一定要折到第一笔年金的前一年。比如本题中，0～3年的等额支出折现时只能折到0的前一年，而现值是在0那点的价值，因此可以有两种处理方法：一种是先整体折到-1年，再往0点折算，比如答案B；另一种处理方法是，将这笔等额支出分成两部分，在0点的不需折现，1～3年的再按年金现值折算，比如答案E；另一个问题是关于公式中n的确定，如果年金数量较少，可以数年金个数，即为n；当年金数量较多时，用最后一笔年金发生的时点减去第一笔年金的前一年，即为n。如本题中5～10年的年金60，折现时需先折算到第5年初(4年末)，则年金个数为10-4=6，然后再从第4年末一次折现到0点。2020教材P162-175

  • 第19题：

    某项目的现金流量图如下图所示。若该项目基准收益率为i，则净现值为()。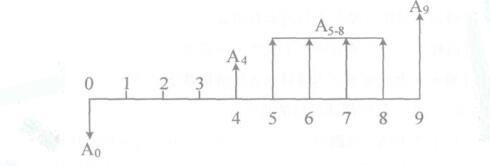

    A.-A0+A4(P/F,i,4)+A5-8(P/A,i,8)+A9(P/F,i,9)
    B.-A0+A4(P/F,i,4)+A5-8(P/A,i,8)(P/F,i,4)+A9(P/F,i,9)
    C.-A0+A4(P/F,i,4)+A5-8(P/A,i,4)(P/F,i,4)+A9(P/F,i,9)
    D.-A0+A4(P/F,i,4)+A5-8(P/A,i,4)(P/F,i,5)+A9(P/F,i,9)

    答案：C
    解析：

  • 第20题：

    某项目建设期2年，建成后年营业收入为A，计算期为10年，折现率为i，关于营业收入的该现金流量，下列说法正确的是（　）。

    • A、营业收入的现值为A(P/A,i.8)
    • B、营业收入的现值为A(P/A,i.10)
    • C、营业收入的现值为A(P/A,i,8)(P/F,i,2)
    • D、营业收入的现值为A(P/A,i.10)(F/P,i,2)

    正确答案:C

  • 第21题：

    若P位于第一年末，F位于第n年初，复利利率为i，则P的表达式是（）

    • A、P=F（P/F，i，n）（F/P，i，1）
    • B、P=F（P/F，I，n）
    • C、P=F（P/F，I，n-2）
    • D、P=F（P/F，I，n-1）（F/P，I，2）

    正确答案:A

  • 第22题：

    多选题
    有一项年金，前2年无流入，后6年每年初流入100元，则下列计算其现值的表达式正确的有（　　）。
    A

    P=100×（P/A，i，6）（P/F，i，2）

    B

    P=100×（P/A，i，6）（P/F，i，1）

    C

    P=100×（F/A，i，6）（P/F，i，7）

    D

    P=100×[（P/A，i，7）-（P/F，i，1）]


    正确答案： A,B
    解析：
    该项年金为递延年金。递延年金是指第一次支付发生在第二期或第二期以后的年金。一般用m表示递延期数，用n表示计息次数。“前2年无流入，后6年每年初流入100元”意味着从第3年开始每年年初有现金流入100元，共6笔，也就是从第2年开始每年年未有现金流入100元，共6笔。因此，递延期m=1，年金个数n=6。因为（P/F，i，1）=（P/A，i，1）。

  • 第23题：

    多选题
    已知从第0年到第n年，每年年值为A，利率为i，期限为n，则现值P为（）。
    A

    A+A（P／A，i，n）

    B

    A（P／A，i，n+1）

    C

    A（P／A，i，n+1）（F／P，i，1）

    D

    A（F／A，i，n+1）（P／F，i，n）

    E

    A（F／A，i，n）（P／F，i，n）


    正确答案： D,A
    解析： 暂无解析

相关内容