有A、B、C、D四个零件，均先在第一台设备上加工，再到第二台设备上加工，各个零件在这两台设备上的加工时间如下表：ABCD第一台设备9368第二台设备10249按约翰逊法则，四个零件最优的加工顺序应为（ ）。A. B—A—C—D B. C—D—A—BC. B—C—D—A D. D—A—C—B
题目
有A、B、C、D四个零件，均先在第一台设备上加工，再到第二台设备上加工，各个零件在这两台设备上的加工时间如下表：
A
B
C
D
第一台设备
9
3
6
8
第二台设备
10
2
4
9
按约翰逊法则，四个零件最优的加工顺序应为（ ）。
A. B—A—C—D B. C—D—A—B
C. B—C—D—A D. D—A—C—B
相似考题
参考答案和解析
正确答案：D
【解析】本题考点约翰逊法则。根据约翰逊法则，先找出所有零件加工的最小值，其出现在B零件的第二台设备上，所以B零件将是最后加工，因此可以排除AC选项。把B零件剔除之后，再找出剩余的三个零件的最小值，其出现在C零件的第二台设备上，所以C零件将会倒数第二个加工，所以此题选D。参见教材P80
更多“有A、B、C、D四个零件,均先在第一台设备上加工,再到第二台设备上加工,各个零件在这两台设备上的 ”相关问题
-
第1题：
两台设备加工同样的零件，第一台出不合格品的概率是2%，第二台出不合格品的概率是3%，若将两台设备加工出来的零件放在一起，且已知第一台加工的零件比第二台加工的零件多1倍，则：
如果任取一个零件是不合格品，则它是第二台机床加工的概率为（ ）。
A. 0.435 B. 0.825 C. 0.977 D. 0.980答案：A解析：P(A2
)=(P(A2)P(
A2))/P（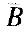
) =((1/3) x0. 03)/(1-0. 977) =0.435。 -
第2题：
两台车床加工同样的零件，第一台出现不合格品的概率是0.03，第二台出现不合格品的概率是0.06，加工出来的零件放在一起，并且已知第一台加工的零件数比第二台加工的零件数多一倍. 1. 求任取一个零件是合格品的概率； 2. 如果取出的零件是不合格品，求它是由第二台车床加工的概率.
0.5 -
第3题：
两台机床加工同样的零件，第一台的废品率为0.04，第二台的废品率为0.07，加工出来的零件混放，假设第一台加工的零件数是第二台的2倍，则任取一零件为合格品的概率为 。
A．0.90
B．0.94
C．0.95
D．0.98
C -
第4题：
两台设备加工同样的零件，第一台出不合格品的概率是2%，第二台出不合格品的概率是3%，若将两台设备加工出来的零件放在一起，且已知第一台加工的零件比第二台加工的零件多1倍，则：
任取一个零件是合格品的概率是（ ）。
A. 0.435 B. 0.825 C. 0.977 D. 0.980答案：C解析：设A1={第一台机床加工}，A2={第二台机床加工}，B ={合格品}，则P(B)=P(A1)P(B A1) +P(A2)P(B A2) = (2/3) x (98/100) + (1/3) x (97/100) =0. 977。 -
第5题：
设有两台机床加工同样的零件，第一台机床出废品的概率是0.03，第二台机床出废品的概率是0.02，加工出来的零件混放在一起，并且已知第一台机床加工的零件比第二台机床多一倍. 则任取一个零件是合格品的概率是（). 若任取的一个零件经检查后发现是废品，则它是第二台机床加工的概率是（).
A．0.923, 0.25
B．0.8, 0.25
C．0.973, 0.75
D．0.973，0.25
(1)0.0267 (2)0.25