在确定总体比例估计中的样本容量时，如果缺少比例的方差，常取比例值为0．5。此题为判断题(对，错)。

题目

在确定总体比例估计中的样本容量时，如果缺少比例的方差，常取比例值为0．5。

此题为判断题(对，错)。

相似考题

1.常用的点估计是用样本均值估计总体均值，用样本比例估计总体比例，用样本方差估计总体方差。（ ）此题为判断题(对，错)。

2.计算样本容量，如果总体比例的值不知道可以用样本比例来代替，或者取总体比例值为0．5，使得π(1-π)达到最大。（ ）此题为判断题(对，错)。

3.在估计总体均值的情况下确定必要样本容量,如果总体方差未知需要进行估计时,可以采取的估计方法有()。A.进行一次小规模的预调查进行估计B.根据历史上的类似调查进行估计C.根据专家意见确定D.将样本比例取为0.5E.无法确定

4.一项研究中要对贫困户的比例进行推断。在95％的置信度下要求误差不超过±3％。采用重置简单随机抽样中，已知z0．025=1．96，则以下说法正确的有( )。A.如果总体中贫困户的比例估计为30％，则必要样本容量为896人B.如果总体中贫困户的比例估计为30％，则必要样本容量为897人C.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人D.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人E.如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算

参考答案和解析
正确答案：√
更多“在确定总体比例估计中的样本容量时,如果缺少比例的方差,常取比例值为0.5。 ”相关问题

  • 第1题：

    在估计总体比例时样本量的确定中，由于总体比例的值是固定的，因而估计误差主要由样本量来确定。

    此题为判断题(对，错)。


    正确答案：√

  • 第2题：

    常用的点估计有（ ）。

    A.用样本均值估计总体均值
    B.用样本比例估计总体比例
    C.用样本方差估计总体方差
    D.用总体均值估计样本均值
    E.有总体方差估计样本方差

    答案：A,B,C
    解析：

  • 第3题：

    计算样本容量，如果总体比例的值未知，可以（ ）。

    A.用样本比例来代替
    B.取总体比例值为0.5，使得π（1-π）达到最大
    C.取总体比例值为0.1，使得π（1-π）达到最大
    D.取总体比例值为0.2，使得π（1-π）达到最小
    E.取总体比例值为0.3，使得π（1-π）达到最小

    答案：A,B
    解析：

  • 第4题：

    在估计总体比例时所需样本量的计算公式为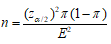

    当总体比例π未知时，就无法根据上述公式确定样本容量。


    答案：错
    解析：

  • 第5题：

    汽车经销商为开发市场欲估计某地区拥有汽车的家庭所占的比例。此项调查要求估计误差不超过0．05，可靠程序为95%，则样本容量（ ）。(注：没有可利用的总体比例百值)[2012年初级真题]



    答案：B,C,E
    解析：
    设E代表允许的估计误差，可以得到估计总体比例时所需的样本量，计算公式为：



    式中，估计误差E由使用者预先确定。大多数情况下。E的取值一般应小于0．1。如果总体比例π的值不知道可以用样本比例P来代替，或者取π=0．5，使得π(1-π)达到最大。

  • 第6题：

    在确定总体比例估计中的样本容量时，如果缺少比例的方差，常取比例值为0．5。
    A.√


    答案：对
    解析：

  • 第7题：

    常用的点估计有（）

    • A、用样本均值估计总体均值
    • B、用样本比例估计总体比例
    • C、用样本方差估计总体方差
    • D、用总体均值估计样本均值
    • E、有总体方差估计样本方差

    正确答案:A,B,C

  • 第8题：

    对于两点分布总体，如果具有“是”值的个体数的比例为p、具有“非”值的个体的比例为q，则有（）

    • A、数学期望为p
    • B、数学期望为q
    • C、方差为p＋q
    • D、方差为pq
    • E、方差为p/q

    正确答案:A,D

  • 第9题：

    判断题
    常用的点估计是用样本均值估计总体均值，用样本比例估计总体比例，用样本方差估计总体方差。（　　）
    A

    对

    B

    错


    正确答案： 对
    解析：
    点估计是用样本统计量的实现值来近似相应的总体参数。总体均值、总体比例、总体方差是三个通常需要被了解的值，因为样本均值、样本比例和样本方差分别是总体均值、总体比例和总体方差的无偏估计，因此由样本值去估计相应的总体值。

  • 第10题：

    多选题
    常用的点估计有（  ）。
    A

    用样本均值估计总体均值

    B

    用样本比例估计总体比例

    C

    用样本方差估计总体方差

    D

    用总体均值估计样本均值

    E

    有总体方差估计样本方差


    正确答案： D,E
    解析：

  • 第11题：

    多选题
    A

    如果总体中贫困户的比例估计为30%，则必要样本容量为896人

    B

    如果总体中贫困户的比例估计为30%，则必要样本容量为897人

    C

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人

    D

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人

    E

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算


    正确答案： D,C
    解析：

  • 第12题：

    多选题
    在确定必要样本容量时，如果总体比例（π）未知，则（    ）。
    A

    无法计算样本容量

    B

    可以取π=0.1

    C

    可以用样本比例代替

    D

    可以取π=0.25

    E

    可以取π=0.5


    正确答案： E,A
    解析：

  • 第13题：

    常用的点估计是用样本均值估计总体均值，用样本比例估计总体比例，用样本方差估计总体方差。（ ）


    答案：对
    解析：

  • 第14题：

    计算样本容量，如果总体比例的值不知道可以用样本比例来代替，或者取总体比例值为0.5，使得π（1-π）达到最大。（ ）


    答案：对
    解析：

  • 第15题：

    一项民意调查中，随机抽取的500人中有390人表示赞成实施新政。则下列说法中正确的有（ ）。

    A．样本比例
    B．在其它条件不变时，样本比例p的方差随着样本容量的增大越来越小
    C．在其它条件不变时，样本比例p的方差随着样本容量的增大越来越大
    D．在其它条件不变时，样本比例p的方差不会随着样本容量的增大而发生改变
    E．在其它条件不变时，样本比例p的方差随着样本容量的增大在某些区间会变大，在某些区间会变小

    答案：A,B
    解析：

  • 第16题：

    在确定必要样本容量时，如果总体比例（π）未知，则（ ）。

    A.无法计算样本容量
    B.可以取π=0.1
    C.可以用样本比例代替
    D.可以取π=0.25
    E.可以取π=0.5

    答案：C,E
    解析：

  • 第17题：

    汽车经销商为开发市场欲估计某地区拥有汽车的家庭所占的比例。此项调查要求估计误差不超过0.05,可靠程度为95%,则样本容量()(注:没有可利用的总体比例π值)

    A.无法确定
    B.计算公式中的π可以采用试验性调查估计的样本比例来代替
    C.计算公式中的π可以取0.5
    D.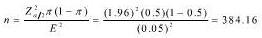,即取384户调查
    E.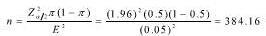,即取385户调查

    答案：B,C,E
    解析：

  • 第18题：

    在总体比例估计时，样本量的确定经常要考虑到总体比例的大小，当总体比例未知时，出于谨慎考虑，一般假定总体比例为（）。

    • A、0
    • B、0.25
    • C、0.5
    • D、0.75

    正确答案:C

  • 第19题：

    已知某简单随机样本中，n=100，其中65人为女性。置信度为95%，Z=1.96。要估计总体中女性的比例，则以下正确的有（）

    • A、样本比例p=0.65
    • B、样本比例p=0.35
    • C、总体比例的置信区间为（55.65%，74.35%）
    • D、样本方差为0.2275
    • E、样本比例的方差为0.2275

    正确答案:A,C,E

  • 第20题：

    多选题
    一项研究中要对贫困户的比例进行推断。在95%的置信度下要求误差不超过±3%。采用重置简单随机抽样中，已知z0.025=1．96，则以下说法正确的有（）。
    A

    如果总体中贫困户的比例估计为30%，则必要样本容量为896人

    B

    如果总体中贫困户的比例估计为30%，则必要样本容量为897人

    C

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人

    D

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人

    E

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算


    正确答案： E,A
    解析： 暂无解析

  • 第21题：

    单选题
    在总体比例估计时，样本量的确定经常要考虑到总体比例的大小，当总体比例未知时，出于谨慎考虑，一般假定总体比例为（）。
    A

    0

    B

    0.25

    C

    0.5

    D

    0.75


    正确答案： B
    解析： 暂无解析

  • 第22题：

    多选题
    对于两点分布总体，如果具有“是”值的个体数的比例为p、具有“非”值的个体的比例为q，则有（）
    A

    数学期望为p

    B

    数学期望为q

    C

    方差为p＋q

    D

    方差为pq

    E

    方差为p/q


    正确答案： B,E
    解析： 暂无解析

  • 第23题：

    多选题
    计算样本容量，如果总体比例的值未知，可以()。
    A

    用样本比例来代替

    B

    取总体比例值为0.5，使得π（1-π）达到最大

    C

    取总体比例值为0.1，使得π（1-π）达到最大

    D

    取总体比例值为0.2，使得π（1-π）达到最小

    E

    取总体比例值为0.3，使得π（1-π）达到最小


    正确答案： B,A
    解析： 暂无解析

相关内容