从甲地到乙地,要从甲地先乘轮船到丙地,再于次日从丙地乘汽车到乙地。一天中,火车有3班,汽车有6班,那么两天中,从甲地到乙地共有________种不同的走法。A．18B．3C．5D．2

题目

从甲地到乙地,要从甲地先乘轮船到丙地,再于次日从丙地乘汽车到乙地。一天中,火车有3班,汽车有6班,那么两天中,从甲地到乙地共有________种不同的走法。

A．18

B．3

C．5

D．2

相似考题

1.从甲地到丙地有4条路,从丙地到乙地有5条路;从甲地到丁地有2条路,从丁地到乙地有4条路,则从甲地到乙地共有________种不同的走法。A．15B．28C．160D．48

2.从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min。甲地到乙地全程是多少？

3.从甲地到乙地的公路，只有上坡路和下坡路，没有平路，一辆汽车上坡时每小时行驶20千米，下坡时每小时行驶35千米。车从甲地开往乙地需9小时，从乙地到甲地需小时，问：甲、乙两地间的公路有多少千米？（ ）A. 300B. 250C. 210D. 200

4.一条船从甲地到乙地要航行4小时，从乙地到甲地要航行5小时（假定船自身的速度保持不变），今有一木筏从甲地漂流到乙地所需小时为（ ）A．12B．40C．32D．30

更多“从甲地到乙地,要从甲地先乘轮船到丙地,再于次日从丙地乘汽车到乙地。一天中,火车有3班,汽车有6班, ”相关问题

  • 第1题：

    从甲地到乙地每天有直达班车4班，从甲地到丙地每天有直达班车5班，从丙地到乙地每天有直达班车3班，则从甲地到乙地共有（ ）不同的乘车法。

    A. 12 种
    B. 19 种
    C. 32 种
    D. 60 种

    答案：B
    解析：
    从甲地到乙地有两种不同路线，即从甲地直接到乙地和先到丙地再到乙地。因此不同的乘车方法共有4 + 5x3 = 19（种）。

  • 第2题：

    从甲地到乙地有2条路可通，从乙地到丙地有3条路可通，从甲地到丁地有4条路可通，从丁地到丙地有2条路可通，那么从甲地到丙地共有（）种不同的走法．

    A.6种
    B.8种
    C.14种
    D.48种

    答案：C
    解析：
    分析：从甲地到丙地共有两类方法：a从甲→乙→丙，此时从甲到丙分两步走，第一步是从甲到乙，有2条路；第二步是从乙到丙有3条路，由分步计数原理知，这类方法共有2×3=6条路．
    b从甲→丁→丙，同理由分步计数原理，此时共有2×4=8条路．
    根据分类计数原理，从甲地到丙地共有6+8=14种不同的走法．

  • 第3题：

    从甲地到乙地每天有直达班车4班，从甲地到丙地每天有直达班车5班，从丙地到乙地每天有直达班车3班，则从甲地到乙地共有（）不同的乘车法。

    • A、12种
    • B、19种
    • C、32种
    • D、60种

    正确答案:B

  • 第4题：

    单选题
    从甲地到乙地，可以乘轮船，也可以乘汽车。一天中，轮船有5班，汽车有2班，那么一天中，乘坐这些交通工具从甲地到乙地共有（　　）种不同的走法。
    A

    2

    B

    3

    C

    6

    D

    7


    正确答案： D
    解析：
    一天中乘轮船有5种走法，乘汽车有2种走法，每一种走法都可以从甲地到乙地，根据加法原理可知，共有5+2=7（种）走法。

  • 第5题：

    一辆汽车将一批货物从甲地送往乙地再返回，甲乙两地相距100千米，
    汽车每小时行驶90千米。汽车开到中途丙地发现有东西落在甲地，立即返回去取，
    然后再送去乙地，最后花了3小时才返回甲地。问丙地距乙地多少千米?

    A: 30千米
    B: 35千米
    C: 65千米
    D: 70千米

    答案：C
    解析：
    3小时走的总路程为甲乙路程的2倍+甲丙路程的2倍，则甲丙相距(90x3—100x2)÷
    2=35千米。则丙地距乙地100-35=65千米，故选C。

  • 第6题：

    从甲地到乙地,水路比公路近40千米,上年10:00,一艘轮船从甲地驶往乙地,下午1:00,一辆汽年从甲地开往乙地,最后船、车同时到达乙地.若汽车的速度是每小时40千米,轮船的速度是汽车的3/5,则甲乙两地的公路长为（ ）

    A.320千米
    B.300千米
    C.280千米
    D.280千米
    E.以上选项均不正确

    答案：C
    解析：
    设公路长为x千米,别水路长为（x-40）千米,轮船的速度为40×3/5=24（千米/小时），设轮船史了t小时。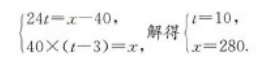

  • 第7题：

    单选题
    从甲地到丙地有两种不同的方案，一种是从甲地经过乙地到丙地，另一种是从甲地直接到丙地。已知从甲地到乙地有3种走法，从乙地到丙地有2种走法，问从甲地到丙地一共有多少种不同的走法？（）
    A

    6

    B

    7

    C

    10

    D

    12


    正确答案： C
    解析： 暂无解析

  • 第8题：

    问答题
    试判断下列各问题是用乘法原理还是用加法原理来解，并写出答案　 （1）从甲地到乙地可以乘火车，也可以乘轮船，还可以乘汽车．一天中有火车6班，轮船3班，汽车4班；一天中从甲地到乙地共有几种不同的走法？　 （2）从3本不同的语文书，4本不同的数学书，5本不同的外文书中任选一本共有几种不同的选法？　 （3）把5只不同的球任意放人4个不同的袋内，共有几种不同的放法？　 （4）加工某零件有三道工序，有8人能做第一道工序，有3人能做第二道工序，有2人能做第三道工序．从中选出3人加工此零件有多少种不同选法？

    正确答案： (1)完成“从甲地到乙地”这件事可以有乘火车、乘轮船、乘汽车这三类彼此独立的方法,因此应当运用加法原理.故不同的走法共有6+3+4=13(种).
    (2)完成“任选一本书”这件事可以有“选一本语文书”、“选一本数学书”、“选一本外文书”这三类方法,因此应当运用加法原理.故不同的选法共有3+4+5=12(种).
    (3)完成“把球放人袋内”这件事必须分五个步骤(即五个球一个一个地放人),因此应该运用乘法原理.故有4×4×4×4×4=1024(种).
    (4)完成“选出3人加工零件”这件事必须分三个步骤(即三道工序都要选出1人).因此用乘法原理,即有8×3×2=48(种).
    解析： 暂无解析

相关内容